Luogu P6880 [JOI 2020 Final] オリンピックバス
P6880 [JOI 2020 Final] オリンピックバス - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
两条前置知识：
- 在图 \(G\) 上构造根为 \(x\) 的最短路树 \(T\)，我们删除任意一条不在 \(T\) 上的边 \(e\)，\(x\) 到任意一个节点 \(u\) 的距离 \(d(x, u)\) 均不会发生变化。
- 有向图上 \(d(i, x)\) 的求法，其中 \(x\) 为定点。实际上就是构造 \(G\) 的反图，在反图上跑 \(x\) 为源点的 dijkstra 即可。
这个题我的第一反应是分层图，把原图分为两层然后两层之间用反边单向导通。也就是这个题。
但是这样可以被 hack，看下面这个例子：
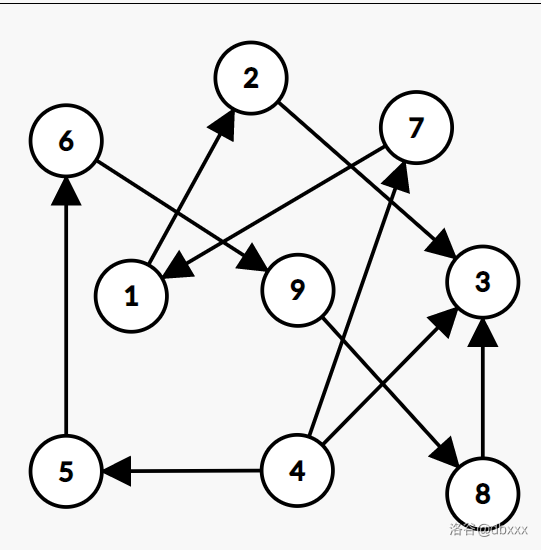
唯一一种可行的走法是：翻转 \(4 \to 3\) 这条边，然后 \(1 \to 2 \to 3 \to 4 \to 5 \to 6 \to 9 \to 8 \to 3 \to 4 \to 7 \to 1\)。
可以看到 \(3 \to 4\) 我们走了两次，分层图不能很好的处理一条道路被翻转然后被走两次（注意到我上面给的另一道题，那个题本身就不允许在一条道路上反走两次，但这个题可以）。
思考发现好像怎么改分层图的模型也不能处理这个问题。先扔在一边。
注意到原题的一个条件：\(n \le 200\)。也就是这个图是稠密的？不过还有一个更强的性质，某棵最短路树最多只有可能有 \(199\) 条边，剩余的边我们都可以利用前置知识第一条加速计算。
实际上翻转一条边 \(e\) 可以看做删除 \(e\) 然后再添加它的反边 \(e'\)。
令 \(e\) 代表 \((u, v, w)\)，\(e'\) 代表 \((v, u, w)\)。再设删除 \(e\) 前 \(s, t\) 两点最短距离 \(d(s, t)\)（也就是原图上 dijkstra 的结果）；删除 \(e\) 后增加 \(e'\) 前 \(s, t\) 两点最短距离为 \(f(s, t)\)；删除 \(e\) 再增加 \(e'\) 后 \(1\) 到 \(n\) 的最短路变为 \(D\)，\(n\) 到 \(1\) 的最短路变为 \(X\)。
那么有：\(D = \min(f(1, n), f(1, v) + w + f(u, n))\)，\(X = \min(f(n, 1), f(n, v) + w + f(u, 1))\)。
证明：\(\min\) 中前半部分为不走 \(e'\) 的最短路，后半部分为必走 \(e'\) 的最短路，合并即可。
现在问题变成：怎么好好利用最短路树性质快速求解 \(f(s, t)\)？事实上我们只关心四种 \(f\)：\(s = 1\) 或 \(s = n\) 或 \(t = 1\) 或 \(t = n\)。
我们令 \(T_1\) 为原图上根为 \(1\) 的最短路树；\(T_n\) 为原图上根为 \(n\) 的最短路树；\(Y_1\) 为反图上根为 \(1\) 的最短路树；\(Y_n\) 为反图上根为 \(n\) 的最短路树。下面的“重新求解”意为，在原图 \(G\) 删除 \(e\) 形成的新图 \(G'\) 上，重新跑 dijkstra 求最短路（其实只要在 \(G\) 上 dijkstra，枚举边时忽略 \(e\) 即可）。
- \(e \in T_1\) 时，\(f(1, t)\) 需要重新求解；否则 \(f(1, t) = d(1, t)\)；
- \(e \in T_n\) 时，\(f(n, t)\) 需要重新求解；否则 \(f(n, t) = d(n, t)\)；
- \(e \in Y_1\) 时，\(f(s, 1)\) 需要重新求解；否则 \(f(s, 1) = d(s, 1)\)；
- \(e \in Y_n\) 时，\(f(s, n)\) 需要重新求解；否则 \(f(s, n) = d(s, n)\)。
由于一棵最短路树上边数最多只有 \(199\)，因此上述算法中最多会跑 \(199 \times 4\) 次 dijkstra，可过。
最后枚举 \(e\)，求最小的 \(D + X + k\) 即可，这里 \(k\) 是原题中的 \(D_i\)：把 \(e\) 翻转的代价。
一些细节：
- 稠密图，dijkstra 不加堆优化（不如不加）。
- 注意到这个题中有重边，而且 \(u \to v\) 中的所有重边并不能简单地只保留最短的那条边 \(ed\)，因为翻转 \(ed\) 之后 \(u \to v\) 还可以从另一条边走，因此这个题不要用邻接矩阵（如果硬用的话需要存 \(u \to v\) 的最短边和次短边，会引入接下来写码中很多容易错的细节）。
- 注意不能通过一条边的两个端点确定这个边是 \(e\)，因为有重边。
- 善用结构体，把图封装起来。
时间复杂度 \(\mathcal{O}(w \times n^3)\)，其中 \(w\) 是一个不超过 \(4\) 的常数。
/*
* @Author: crab-in-the-northeast
* @Date: 2022-10-11 22:33:15
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2022-10-12 03:10:21
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool flag = true;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-')
flag = false;
ch = getchar();
}
while (isdigit(ch)) {
x = (x << 1) + (x << 3) + ch - '0';
ch = getchar();
}
if(flag)
return x;
return ~(x - 1);
}
typedef std :: pair <int, int> pii;
const int maxn = 205;
const int maxm = (int)5e4 + 5;
int fru[maxm], tov[maxm], wei[maxm], ext[maxm];
int n;
struct graph {
graph() {
std :: memset(ont, false, sizeof(ont));
std :: memset(pre, 0, sizeof(pre));
}
int s;
std :: vector <pii> G[maxn];
inline void add_edge(int u, int v, int id) {
G[u].emplace_back(v, id);
}
int d[maxn], dis[maxn], pre[maxn];
bool ont[maxm], vis[maxn];
inline void dijkstra(int ban) {
std :: memset(dis, 0x3f, sizeof(dis));
std :: memset(vis, false, sizeof(vis));
dis[s] = 0;
for (int i = 1; i <= n; ++i) {
int u = n + 1;
for (int j = 1; j <= n; ++j)
if (!vis[j] && dis[j] < dis[u])
u = j;
if (u == n + 1)
break ;
vis[u] = true;
for (pii e : G[u]) {
int v = e.first, id = e.second, w = wei[id];
if (id == ban)
continue;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if (ban)
continue;
ont[pre[v]] = false;
pre[v] = id;
ont[pre[v]] = true;
}
}
}
if (!ban)
std :: copy(dis + 1, dis + 1 + n, d + 1);
}
inline int get(int x, int id) { // 删除 id 后 s 到 x 的距离
if (!ont[id])
return d[x];
dijkstra(id);
return dis[x];
}
} G1, Gn, R1, Rn;
inline bool gmi(int &a, int b) {
return b < a ? a = b, true : false;
}
inline int min(int a, int b) {
return a < b ? a : b;
}
signed main() {
n = read();
int m = read();
G1.s = R1.s = 1;
Gn.s = Rn.s = n;
for (int i = 1; i <= m; ++i) {
int u = read(), v = read(), w = read(), ex = read();
G1.add_edge(u, v, i);
Gn.add_edge(u, v, i);
R1.add_edge(v, u, i);
Rn.add_edge(v, u, i);
fru[i] = u;
tov[i] = v;
wei[i] = w;
ext[i] = ex;
}
G1.dijkstra(0);
Gn.dijkstra(0);
R1.dijkstra(0);
Rn.dijkstra(0);
int ans = G1.d[n] + Gn.d[1];
for (int i = 1; i <= m; ++i) {
int u = fru[i], v = tov[i], w = wei[i], ex = ext[i];
gmi(ans,
min(G1.get(n, i), G1.get(v, i) + w + Rn.get(u, i)) +
min(Gn.get(1, i), Gn.get(v, i) + w + R1.get(u, i)) + ex
);
}
if (ans >= G1.dis[n + 1])
puts("-1");
else
printf("%lld\n", ans);
return 0;
}
