[luogu p5677] 配对统计
\(\mathtt{Link}\)
\(\mathtt{Description}\)
给定一个序列 \(a\) ，定义 \((x, y)\) 为好的配对当且仅当 \(1\le x, y \le n, x \ne y\) 且对于 \(\forall i \in \{1, 2, \ldots, x - 1, x + 1, \ldots, n\}\) 有 \(|a_x - a_y| \le |a_x - a_i|\)。给定 \(m\) 组询问，每组询问给定 \(l, r\)（\(1 \le l \le r \le n\)），查询 \([ l, r]\) 中有多少好的配对。
\(\mathtt{Data} \text{ } \mathtt{Range} \text{ } \mathtt{\&} \text{ } \mathtt{Restrictions}\)
- \(1 \le n, m \le 3 \times 10^5\)
- \(1 \le a_i \le 10^9\)
- \(\forall i \ne j, a_i \ne a_j\)
\(\mathtt{Solution}\)
处理好的配对
首先可以观察到，题目对于好的配对的描述其实就是说 \(a_y\) 对于 \(a_x\) 而言是整个数列中差最小的。很自然想到排序，排序后好的配对一定会相邻。需要注意的是，排序时应该采用结构体，才能保护好数列中每一个数的位置信息。其次注意原题的数据已经给出了每个数不同的限定。
排序后，设排序后的下标是 \(i\)，排序前的位置是 \(pos_i\)，对于每个数进行判断：
- \(a_i - a_{i - 1} < a_{i +1} - a_i\)，那么 \((pos_i, pos_{i - 1})\) 便是一组好的配对；
- \(a_{i +1} - a_i < a_i - a_{i - 1}\)，那么 \((pos_i, pos_{i + 1})\) 便是一组好的配对；
- \(a_{i +1} - a_i = a_i - a_{i - 1}\)，那么 \((pos_i, pos_{i - 1}), (pos_i, pos_{i + 1})\) 两组均为好的配对。
需要注意的是，对于好的配对 \((x, y)\)，\((y, x)\) 不一定是好的配对！比如 \(3, 1, 4\)，\((2, 1)\) 就是好的配对，而 \((1, 2)\) 不是。但是在这里，如果好的配对 \((x, y)\) 有 \(x > y\)，那么我们将 \(x, y\) 进行调换，以 \((y, x)\) 的形式记录为好的配对。虽然 \((y, x)\) 本质上并不是好的配对，但这种记录方式完全不会影响答案。非得这么记录也不是吃饱了撑的，这是便于后面的处理，请接着往下看。
统计好的配对
上面我们已经处理好了好的配对信息，那么接下来进入第二部分，统计好的配对。
首先我们会发现，直接将所有好的配对统计进去很难用树状数组处理。又观察到题目中所给的操作只有查询，没有增删改。不免想到HH的项链，一切似乎都告诉我们，正解应该是将查询离线。
先考虑将查询按照r第一关键字l第二关键字从小到大排序，这样，每次查询都相当于查询右边界r在不断向右挪动。
不妨假想一个数组 \(b_i\) 表示左端点 \(l \le i\) 的好的配对个数。每次扫到一个询问，首先把右边界向右挪动到当前询问的右边界，挪动的过程中可能会扫过一些好的配对的右边界，此时我们考虑将这样的好的配对选中，将这样选中的好配对数量统计起来，再减去 \(b_{l -1}\)，也就是扣除左边界在要查询左边界之外的不符合条件的好的配对。
所以还需要提前将好对也按照右边界第一左边界第二排一下序……
下面是来自zhr的博客的图例
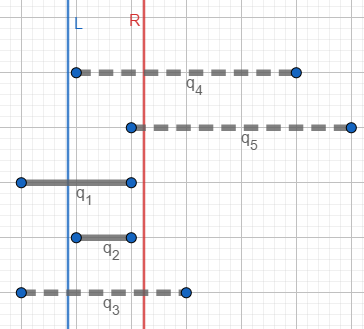
实线就是当前选中的好的配对，虚线就是未选中的好的配对（因为当前右边界还没有扫到这些配对的右边界）。同时我们可以发现 \(q_1\) 的左边界在查询左边界之外，所以实际统计数量还需要把这条线段扣去。（\(b_{l-1}\)）
\(b\) 数组怎么维护呢？想必聪明的你已经想到，用树状数组简单维护一下即可。
\(\mathtt{Time} \text{ } \mathtt{Complexity}\)
处理好的配对时间复杂度 \(\mathcal{O}(n\log n)\)。（排序 \(\mathcal{O}(n\log n)\)，预处理好对 \(\mathcal{O}(n)\)）
统计好的配对时间复杂度 \(\mathcal{O}((m+n)\log n)\)。（\(\log n\) 在树状数组上）
\(\mathtt{Code}\)
/*
* @Author: crab-in-the-northeast
* @Date: 2022-02-27 20:49:14
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2022-02-27 22:25:20
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#define int long long
inline int read() {
int x = 0;
bool flag = true;
char ch = getchar();
while (ch < '0' || ch > '9') {
if (ch == '-')
flag = false;
ch = getchar();
}
while (ch >= '0' && ch <= '9') {
x = (x << 1) + (x << 3) + ch - '0';
ch = getchar();
}
if (flag)
return x;
return ~(x - 1);
}
const int maxn = 300005;
const int maxm = 300005;
int n, m;
inline int lowbit(int x) {
return x & -x;
}
struct number {
int v, pos;
const bool operator < (const number b) {
return this -> v < b.v;
}
}a[maxn];
struct pair {
int l, r;
const bool operator < (const pair b) {
if (this -> r != b.r)
return this -> r < b.r;
return this->l < b.l;
}
}p[maxn * 2];
int pcnt;
inline void insert_pair(int l, int r) {
l = a[l].pos;
r = a[r].pos;
if (l > r)
l ^= r ^= l ^= r;
p[++pcnt].l = l;
p[pcnt].r = r;
}
struct question {
int l, r, pos;
const bool operator < (const question b) {
if (this -> r != b.r)
return this -> r < b.r;
return this->l < b.l;
}
}q[maxm];
int c[maxn];
void add(int x) {
for (; x <= n; x += lowbit(x))
++c[x];
}
int query(int x) {
int ans = 0;
for (; x; x -= lowbit(x))
ans += c[x];
return ans;
}
signed main() {
n = read();
m = read();
if (n == 1) {
puts("0");
return 0;
}
for (int i = 1; i <= n; ++i) {
a[i].v = read();
a[i].pos = i;
}
std :: sort(a + 1, a + 1 + n);
insert_pair(1, 2);
insert_pair(n - 1, n);
for (int i = 2; i < n; ++i) {
int dl = a[i].v - a[i - 1].v, dr = a[i + 1].v - a[i].v;
if (dl <= dr)
insert_pair(i, i - 1);
if (dl >= dr)
insert_pair(i, i + 1);
}
std :: sort(p + 1, p + 1 + pcnt);
for (int i = 1; i <= m; ++i) {
q[i].l = read();
q[i].r = read();
q[i].pos = i;
}
std :: sort(q + 1, q + 1 + m);
int ans = 0;
for (int i = 1, j = 1; i <= m; ++i) {
for (; j <= pcnt && p[j].r <= q[i].r; ++j)
add(p[j].l);
ans += q[i].pos * (j - query(q[i].l - 1) - 1);
}
printf("%lld\n", ans);
return 0;
}
\(\mathtt{More}\)
本题最大亮点离线。
