[luogu p5410] 【模板】扩展 KMP（Z 函数） & 扩展 KMP（Z 函数）学习笔记
Z函数 & exKMP
P5410 【模板】扩展 KMP（Z 函数） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
我的 \(z\) 函数和流行版本不太相同，相对而言，更短小精悍且易懂。
概念与约定
本文字符串从 \(1\) 开始编号。
下文中有些概念是我的自定义概念。
字符串的第 \(i\) 个后缀：从第 \(i\) 个字符开始一直到末尾形成的子字符串。
定义 \(z(i)\) 表示字符串与它第 \(i\) 个字符开始的后缀的最大公共前缀长度。 考虑到 \(z(1)\) 的特殊性，其值可以为 \(0\)，也可以为 \(|S|\)，本文的算法中需要令 \(z(1) = 0\).
\([l, r]\) 表示字符串从第 \(l\) 个字符到第 \(r\) 个字符连接形成的子串；\([x]\) 表示字符串的第 \(x\) 个字符。
\(z\) 函数算法可以做到在 \(\operatorname{O}(|S|)\) 复杂度内完成 \(z(i)(2 \le i \le |S|)\) 的求解。
算法讲解
\(z\) 函数
既然 \(z\) 函数是 exKMP 的核心部分，自然和 KMP 的核心部分——求 \(\pi\) 数组（别名很多，fail、nxt、……）相似，都是从向后递推，用前面的 \(z\) 函数值推导后面的 \(z\) 函数值。
现在假设我们要求 \(z(x \ge 2)\)，自然地，\(z(1) \cdots z(x-1)\) 的 \(z\) 函数值都已知了。我们随便取一个 \(1 \le k < x\)，记 \(p = k + z[k] - 1\)。
根据定义可以得到 \([k, p] = [1, z(k)]\)，如下图蓝色部分所示：
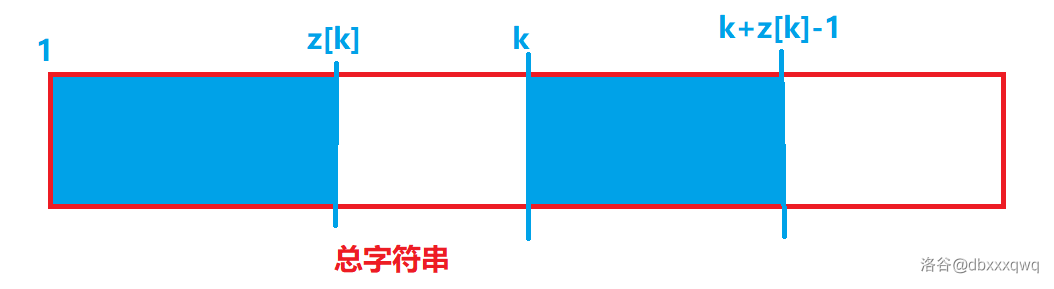
当然了，\(x > k\)，因此 \(x\) 应该表示在 \(k\) 的右边，现在我们来表示一下它。我们知道，两个蓝色区域是完全相同的，因此两个蓝色串其中，相对位置一样的子串，也应该完全相同，于是有 \([x, p] = [x - k + 1, z(k)]\)，如下图橙色部分所示：
对了，那有些人会问了，\(x\) 会不会超过 \(p\) 啊？这点我们最后再提，先看现在 \(x\) 比较正常，在第二块蓝色色块上的图：
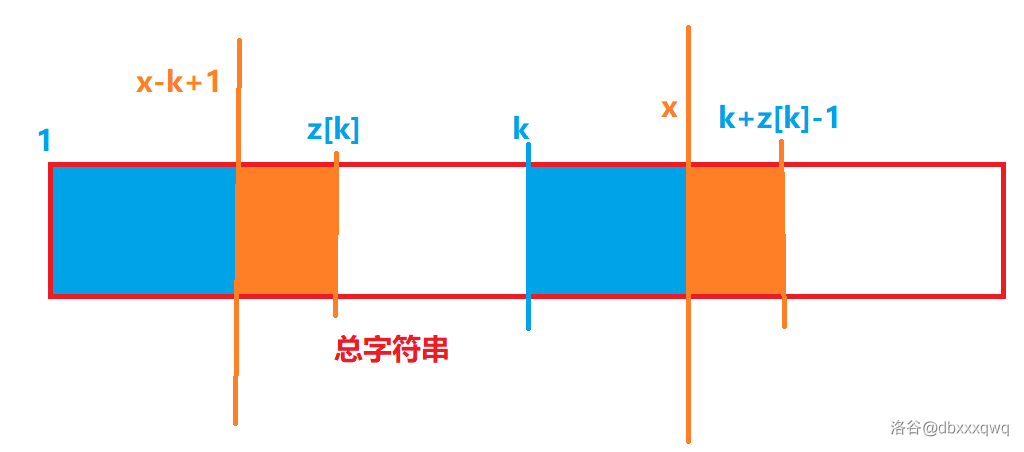
令 \(l = z(x - k + 1)\)，可以得到 \([x-k+1, x-k+l] = [1, l]=[x, x+l-1]\)，先上图再解释：
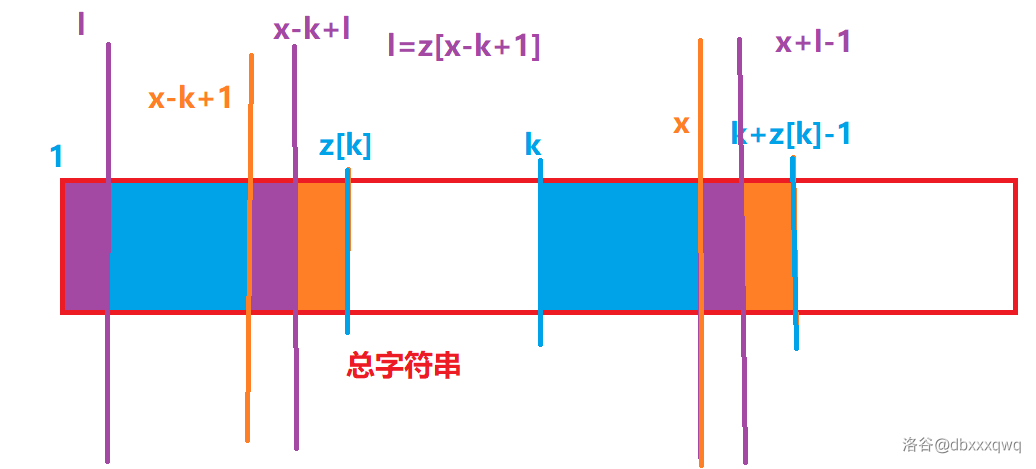
上图的紫色部分就是刚刚说的三个相等的子串。其中：
\([x-k +1, x - k + l]\) 和 \([1, l]\)，即前两个紫色块，他们完全相同的原因是 \(z\) 函数的定义；
\([x-k+1, x-k+l]\) 和 \([x, x+l-1]\)，即后两个紫色块，他们完全相同的原因：这两个紫色块是原来的两个橙色块中相对位置相同的子串。请注意这里相同的原因。
综上可以得到三个紫色块完全相同。
好的，观察这个图片，已经可以得到结论：\(z(x) = l = z(x - k + 1)\)，接下来开始解释。
我们考虑上面三根紫线分别紧挨着的后面的字符，它们分别是：\([l + 1]\)，\([x - k + l + 1]\)，\([x + l]\)。
首先可以证明：\([l + 1]\) 和 \([x - k + l +1]\) 不同。因为如果他们俩相同，那么根据 \(z\) 函数的定义，代表紫色区块的 \(z(x - k +1)\) 绝对还可以再扩大，而事实上没有。
其次可以看出：\([x - k + l + 1]\) 和 \([x + l]\) 相同，因为它们是原来两个橙色块中相对位置相同的字符。同时也请注意这里相同的原因。
因此可以得到：\([l +1]\) 和 \([x + l]\) 不同。
于是就能证明：原串和 \([x, |S|]\) 的最长公共前缀也是紫色部分。因为紧接着接下来那个字符就不同了嘛。
因此答案是 \(z(x) = l = z(x - k + 1)\).
那么结束了吗？其实并没有。因为上述的图中我们可以得到这样一个结论，需要一个重要的地方做支撑：\(l\) 要严格小于原来的橙色块的长度 \(k + z[k] - x\)，也就是紫色块不可以淹没橙色块。为什么？让我来看一下这种紫色淹没橙色的情况（我规定刚刚那种是第一种情况，现在这种是第二种）：
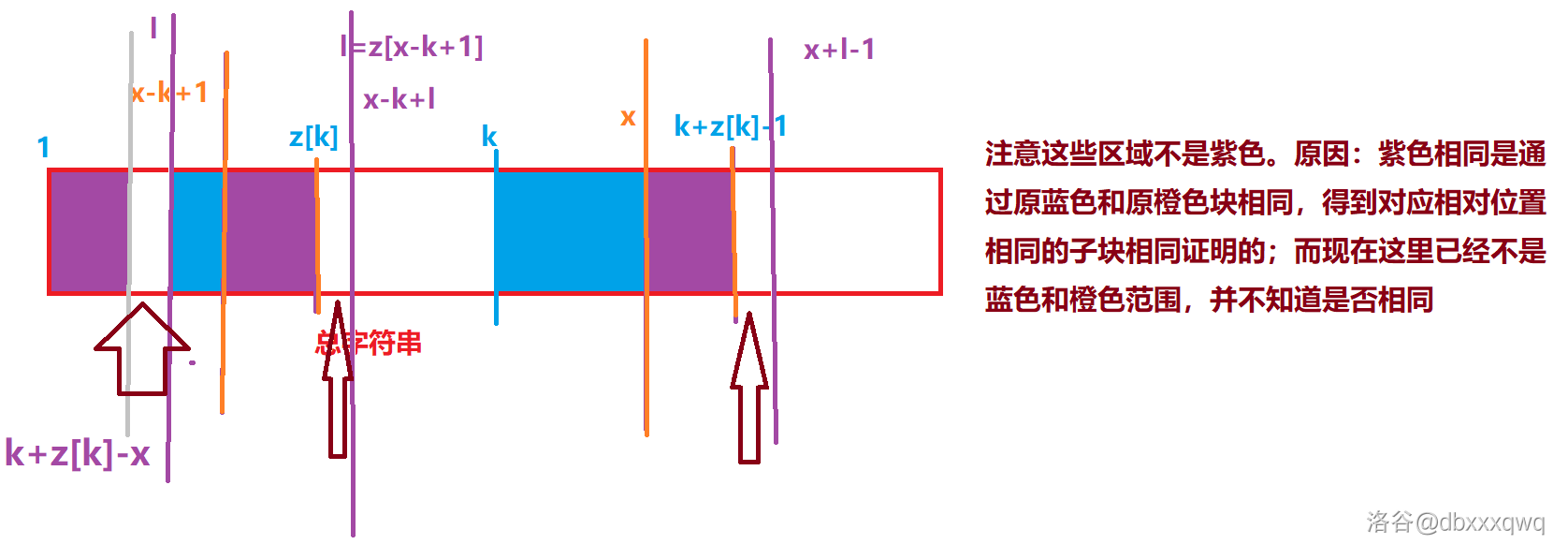
不难发现这时，紫色完全淹没了橙色。与第一种情况不同，此处箭头指向的三个区域中，前两个箭头所指区域仍然保证相同，但和三个区域不再保证相同。前两块相同仍然因为 \(z\) 函数的定义，这点无影响；而原先关于第二个区域和第三个区域相同的证明此处不再成立，因为原先的证明依赖【这两块是原橙色部分的相同位置子串】，而此处这两块因为逾越了橙色块，所以不是。
因此我们现在只能下结论说 \(z(x) \ge k + z(k) - x\)，\(k + z(k) - x\) 即上面三个紫色块的长度。为了确定 \(z(x)\) 的具体值，我们需要从 \([k + z(k) - x + 1]\)（第一个紫色块右方）和 \([p +1 = k + z(k)]\)（第三个紫色块右方）分别维护两个指针，同步向右走，暴力判断字符是否相等，给 \(z(x)\) 暴力地不断自增 \(1\)。
总结一下：
- \(z(x - k + 1) < k + z(k) - x\) 时，\(z(x) = z(x - k + 1)\)；
- 否则，初始令 \(z(x) = k + z(k) - x\)，然后暴力判断字符累加 \(z(x)\)。
恭喜你，已经学会了 \(z\) 函数，但是或许你会有疑虑，这样的做法真的是线性吗？事实上，只要我们改动一下，不随便地选取 \(k\)，而是令 \(k\) 初始时为 \(1\)，然后每次在第二种情况后令 \(k \gets x\) 就可以得到线性复杂度了（第一种情况后 \(k\) 不变）。这里就是和网上的流行版本不同的地方了，网上流行版本需要将 \(k\) 设置为 \(k + z[k] - 1\) 最大的那个，事实上不太直观，不易于理解而且相对麻烦。
第一种情况显然是 \(\mathcal{O}(1)\)，而此时，第二种情况均摊后也是线性的，原因是，观察到第二种情况中我们暴力判断字符的过程，右侧那个字符始终从 \([p + 1]\) 开始向右判断，最终结束后，\(p\) 又会被赋为当前的 \(x + z(x) - 1\)，所以放眼全局，我们暴力判断的右侧那个字符从左到右扫过一次，换句话说，我们全局上最多只会暴力判断 \(|S|\) 次。所以均摊也是线性的。
最后来到了喜闻乐见的细节：\(x\) 会不会超过 \(p\) 呢。其实是有可能的，这时候一定走第二种情况。细节问题在于此时算出的 \(z(x)\) 最小值等于 \(p - x + 1\)，由于 \(x\) 超过 \(p\) 甚至可以算出负数，这肯定不是我们想要的。因此在 \(z(x) \leftarrow p - x + 1\) 时，要注意判断如果 \(z(x) < 0\)，要使 \(z(x) \gets 0\).
代码（事实上没有注释后相当短小好记）：
void get_z(char *P) {
int m = strlen(P) - 1; // 注意，这里的 m 其实就是字符串 P 的长度，只是我从 1 开始，因此 strlen 得到的长度会多 1
for (int i = 2, k = 1; i <= m; ++i) {
if (k + z[k] - i <= z[i - k + 1]) { // 第二种情况
// 相当于 z[i - k + 1] >= k + z[k] - i
// 也就是补齐后的紫色大于等于橙色时，进入第二种情况
z[i] = k + z[k] - i; // 将z[i] 调到 k + z[k] - i，这是它的最小值
if (z[i] < 0) // 判断，防止负数出现
z[i] = 0;
while (i + z[i] <= m && P[z[i] + 1] == P[i + z[i]])
++z[i]; // 暴力枚举，判断字符相等
k = i; // 直接令 k = i
} else
z[i] = z[i - k + 1]; // 第一种情况
}
z[1] = m; // 题目中要求 z[1] = m，在算法处理后赋值
return ;
}
exKMP
exKMP 也就是求模式串 \(P\) 在文本串 \(T\) 的每个后缀中的最长公共前缀，其实原理本质还是 \(z\) 函数。
一种做法：令 \(S' = P + c + T\)，其中 \(c\) 是 \(P\) 和 \(T\) 中均不含有的字符，然后对 \(S'\) 进行 \(z\) 函数，就是答案。具体正确性在此不证明（因为比较直观易懂），其实中间就是起到一个隔离符的作用，让 \(z\) 函数求解算法不会将 \(P\) 和 \(T\) 做拼在一起子串等的行为，导致错误结果。
还有一种做法（真正的exKMP），只需要在 \(z\) 函数算法基础上，将几个 \(z\) 替换为 \(e\)，再把字符串分裂开：
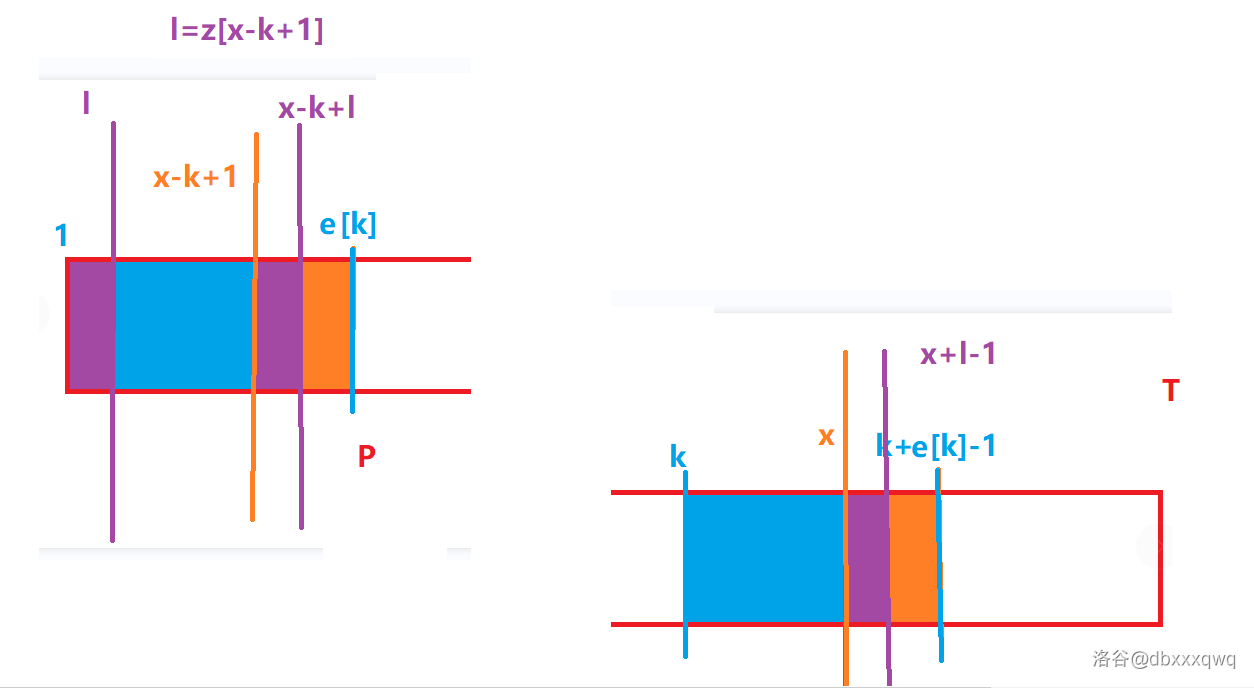
需要提前预处理出 \(P\) 的 \(z\) 函数。
代码：
void exkmp(char *T, char *P) {
int n = strlen(T) - 1, m = strlen(P) - 1; // 同上，注意这里 n 和 m 就是分别实际的文本串和模式串的长度
for (int i = 1, k = 0; i <= n; ++i) { // 注意哪些地方换成了 p（也就是刚刚我说的 e），哪些还是原来的 z
// 这里让 k = 0，一定会走到第二种情况暴力判断，然后 k = 1 就正常了
if (k + p[k] - i <= z[i - k + 1]) {
p[i] = k + p[k] - i;
if (p[i] < 0)
p[i] = 0;
while (i + p[i] <= n && p[i] < m && P[p[i] + 1] == T[i + p[i]])
++p[i];
k = i;
} else
p[i] = z[i - k + 1];
}
return ;
}
后话
洛谷该题目模板中，最高赞的一篇题解是 George1123 写的 \(z\) 函数，纯推的式子非常易懂。唯独可惜的是中间推理，红色括号中的条件是错误的（多了个等号）；同时最后关于线性复杂度的证明其实有点问题，或者没说明白为什么每个字符不会被暴力判断多次（因为 \(z\) 函数中有两种情况）。其他题解的问题就更多了，所以我就想写一篇这样详尽的题解，尽我可能做到最好地达到讲授传达到的目的。
模板洛谷 P5410。
谢谢。
