P5372 SNOI2019 积木
不难想到图论建模（也没啥别的思路了），考虑用一张图刻画网格板上的任意一种状态：
- 图有 \(n \times m\) 个点，形成点阵，和网格板对应。
- 网格板上，一个积木对应一条边，积木占据的两个格子，对应这条边连接的两个点。
比如第一个样例中，起始时的网格板状态：
3 3
nnn
uuu
o<>
刻画为下面的图论模型：
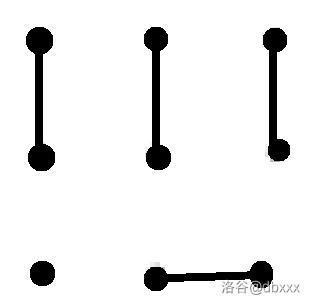
我们试图发掘这样刻画出的图的性质。容易发现，这样刻画出的任何一种图，都是一个边数为 \(\dfrac{n \times m - 1}2\) 的匹配（即任意两条边中的四个端点互不相同），因为原图中一个格子上显然不可能有两块积木。
我们再试图刻画积木的移动。观察题目中的移动方式，形象地说，这种移动方式像是空位在它的上下左右四个方向中，选择一块毗邻的积木，然后把他“拽”下来。这种理解也恰好和方案的输出方式相吻合。而且，无论与空位毗邻的那个积木处于东西走向还是南北走向，它总是可以被移动。
于是可以发现，在图上，积木的移动可以刻画为：
- 在代表唯一空位的孤立点 \(u\) 的上下左右四个点中，选择一个点 \(v\)。设 \(v\) 原来与 \(w\) 相连，即 \(v - w\) 原来是一块积木。
- 断开 \(v - w\)，连接 \(u - v\)，代表 \(v - w\) 这块积木被拽到了 \(u - v\)。
- 此时，\(w\) 变成了新图上的空位。
下图是两个例子。
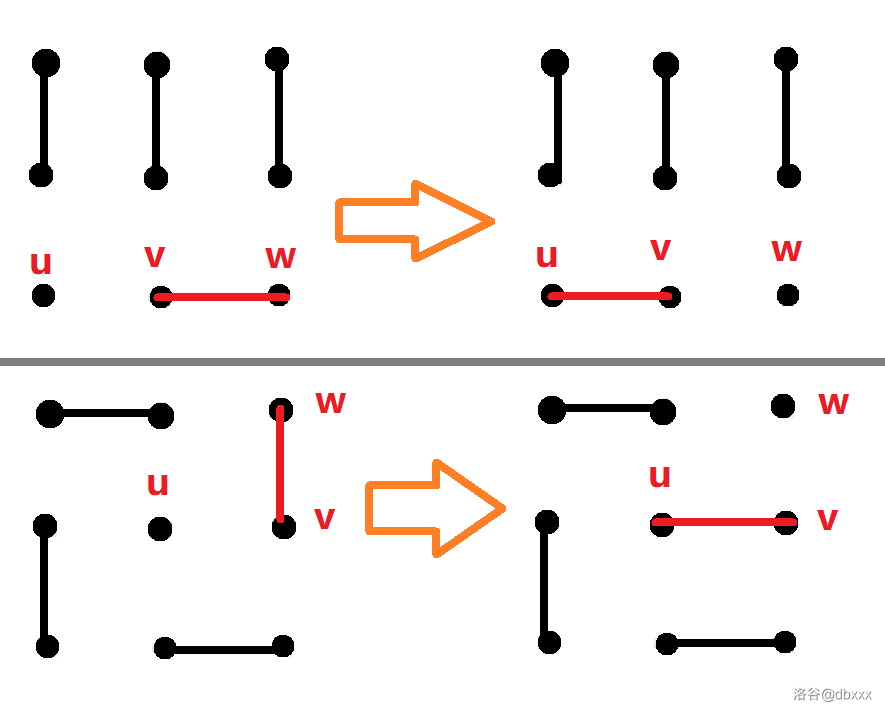
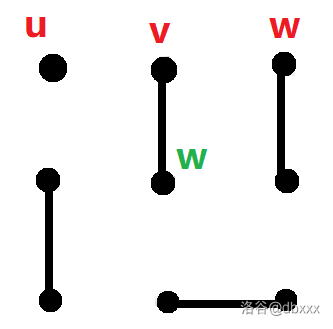
注意，上面只有点 \(v\) 是主动选择的，点 \(w\) 会被被动选择为与 \(v\) 相连接的点，它在 \(v\) 被选择后已经唯一。这里 \(\boldsymbol w\) 不能随便选择一个与 \(\boldsymbol v\) 相连接的点。比如下面红色的 \(w\) 选择就是不合法的，正确应该是绿色的 \(w\)。
这里，我用另一种角度理解上面的刻画：先让空位 \(u\) 移动到 \(v\)，在原图上加上 \(u - v\) 这条边，再让空位从 \(v\) 移动到 \(w\)，从原图上抹去 \(v - w\) 这条边。
这种角度有助于理解多次连续的移动。事实上，多次连续的移动就是上面操作步骤的重复，\(k\) 次操作可以拆成 \(2k\) 次空位的移动，其中第 \(2i - 1\) 次移动和第 \(2i\) 次移动对应第 \(k\) 次操作：第 \(2i - 1\) 次移动加边，第 \(2i\) 次移动删边。
这里我再换一种角度理解加边 / 删边。我们将点阵看成一个完全的网格图，即任意上下相邻，左右相邻的两个点之间都有边，只不过边有虚实两种状态，如果一条边上有一个积木（也即原来对边的定义），则这条边是实边，否则这条边是虚边。这样以来原来的加边 / 删边就变成对边的实虚切换。
问题转化成，给定一个完全网格图，初始边集 \(S\) 中的边是实边，你的目标是将整张图中的实边构成边集 \(T\)（\(S\) 和 \(T\) 都构成大小为 \(\dfrac{n \times m - 1}2\) 的匹配）。能否构造出一个长度为偶数且不超过 \(1.6 \times 10^7\) 的路径，满足以下要求：
- 路径起点为初始网格图中，唯一的不属于任意打开的边的点（也即唯一一个不在 \(S\) 中的点）。
- 一个点从路径起点出发，沿着路径走。每走一条边，这条边的虚实状态改变。
- 这条路径的第偶数步一定走的是一条实边。
- 沿着路径走完后，整张图边的实边集合变为 \(T\)。
这里不用限制路径的第奇数步一定走虚边，因为每次第奇数步之前，\(u\) 应该走到的都是一个空位点，该点恰满足不属于任意一个实边，所以接下来想走一定要走虚边。然而，第偶数步要做限制，原理类似于上面举过的反例。
这里有一个小套路，对于有初始态和目标态开关切换问题，设 \(U\) 为元素全集，\(S\) 为初始态中打开的元素，\(T\) 为目标态中打开的元素，则等价于 \(S \oplus T\) 中的元素要被切换奇数次，\(U \setminus (S \oplus T)\) 中的元素要被切换偶数次，从而将限制转化地更容易处理。
\(S \oplus T\) 中的 \(\oplus\) 是对称差运算，它恰好包含在 \(S\) 和 \(T\) 中恰出现一次的元素。在开关切换问题中，该集合中的元素等价于初始态和目标态开关状态不同的元素，显然它们需要被切换奇数次，而剩余的自然要被切换偶数次。
在本题中，目标态的要求就可以被刻画为：路径要满足 \(S \oplus T\) 中的边经过奇数次，其它边要经过偶数次。
于是我们考察 \(S \oplus T\) 这个边集看能得到什么。
如果一个点 \(u\) 在 \(S\) 和 \(T\) 中都有出现：
- 如果 \(u\) 在 \(S\) 和 \(T\) 中，分别连出的实边不同（即连接的不是同一个点），则 \(S \oplus T\) 中这两条实边都会保留，\(u\) 在 \(S \oplus T\) 中恰连着 \(2\) 条实边，度数为 \(2\)。
- 如果 \(u\) 在 \(S\) 和 \(T\) 中，分别连出的实边相同（即连接的是同一个点），则 \(S \oplus T\) 中这两条边都会消失，没有与 \(u\) 相关联的边。
然后分类讨论：
- 如果 \(S\) 和 \(T\) 中，那个没出现的点不同：设 \(s\) 为 \(S\) 中没出现的点，因为 \(s\) 在 \(T\) 中恰连着一条实边，因此 \(S \oplus T\) 中这条实边将被保留，\(s\) 的度数为 \(1\)。同理，\(T\) 的孤立点 \(t\) 的度数也为 \(1\)。
- 此时因为 \(S \oplus T\) 中出现的点里，除了 \(s\) 和 \(t\) 度数为 \(1\) 以外其余度数均为 \(2\)，所以 \(S \oplus T\) 由一堆环和 \(s - t\) 的一条链构成，并且这些链和环之间互不相交。
- 如果 \(S\) 和 \(T\) 中，没出现的点相同：显然 \(S \oplus T\) 中没有与这个孤立点相关联的边。
- 此时因为 \(S \oplus T\) 中出现的点的度数都是 \(2\)，所以 \(S \oplus T\) 就是一堆互不相交的环的集合。
- 可以理解为上面那种情况中，因为 \(s = t\) 所以链消失的特殊情况。
后面我们会证明一些性质，这个基本定义会多次用到，请留意：\(S \oplus T\) 中的元素要么来自 \(S\)，要么来自 \(T\)，且只能来自一个。
本题中的 \(S\) 和 \(T\) 都是匹配，所以对于 \(S \oplus T\) 的任意两条毗邻的边 \(e_1\) 和 \(e_2\)，它们之间一定恰有一个来自 \(S\)，恰有一个来自 \(T\)。否则，不妨设它们都来自于 \(S\)，则与 \(S\) 是匹配相矛盾。
所以 \(S \oplus T\) 中，出现的那条 \(s - t\) 的链，设为 \(s - u_1 - u_2 - \ldots - u_k - t\)。那么有：
- \((s, u_1) \in T\)。
- 考虑 \(s\) 的定义，\(s\) 不在 \(S\) 中，所以 \((s, u_1) \not\in S\)，所以 \((s, u_1) \in T\)。
- \((u_1, u_2) \in S\)，\((u_2, u_3) \in T\)……\(s - t\) 这条链是 \(S\)、\(T\) 相间的。
- 根据 \(S \oplus T\) 任意毗邻边不属于同一集合的性质。
- \((u_k, t) \in S\)。
- 考虑 \(t\) 的定义，原理同第一条。
- \(s - t\) 的长度是偶数。
- 根据上面三条可以推出。
然后考虑 \(S \oplus T\) 中的环，这些环也是 \(S\)、\(T\) 相间的，原理同上。所以，这些环的长度都是偶数（否则无法 \(S\)、\(T\) 相间）。
那么 \(S \oplus T\) 的性质都被扒得差不多了，可以开始构造路径了。注意，原题除了经过次数奇偶限制（下简称奇偶限制），还有第偶数次必须经过实边的限制（下简称偶实限制），以及长度限制，我们都要留意。
路径从 \(s\) 开始，我们自然先考虑把 \(s - t\) 这条链走完，于是这条链的奇偶限制就解决了。考虑偶实限制，根据之前证明的性质，第偶数次经过的边一定属于 \(S\)，即开始时一定打开。而这条链上每一条边我们都是第一次走，所以第偶数次经过一条边之前该边一定仍保持打开，满足偶实限制。
接下来考虑环必须走奇数次怎么处理。先来看某一个环怎么处理，如果某一个环可以处理，其它环也就能处理了。下称 \(S \oplus T\) 上的边为关键边。
\(t\) 不和这个环通过关键边相连，为了从 \(t\) 到达环，我们势必要走一部分关键边的同时（这部分可以没有），再走一部分非关键边（这部分必须有）。称这些边为桥梁边。但是我们并不期望更改这些桥梁边的奇偶性（这次我们只想更改目标环上的奇偶性），所以我们考虑通过桥梁边到达环，将环走一遍后，再通过桥梁边返回 \(t\)，这样所有桥梁边经过 \(2\) 次，奇偶性不变。
对于多个环的情况，我们并不一定每次都要回到 \(t\)，可以通过上一个环的桥梁边回溯一部分之后，再 dfs 出一条新的桥梁边去另一个环，从而解决问题。比如：
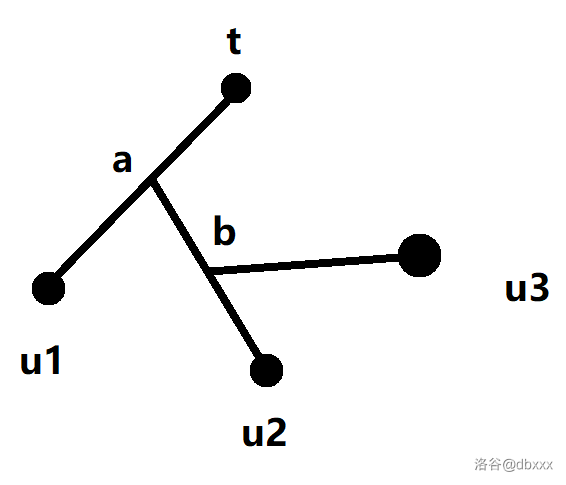
这张图我们忽略原图上的点的方阵性，只是个示意图。\(u_1\)，\(u_2\)，\(u_3\) 为三个仍然在 \(S \oplus T\) 上构成环的点，我们 dfs 找环的过程为：\(t \rightsquigarrow a \rightsquigarrow u_1 \rightsquigarrow a \rightsquigarrow b \rightsquigarrow u_2 \rightsquigarrow b \rightsquigarrow u_3 \rightsquigarrow b \rightsquigarrow a \rightsquigarrow t\)。类似于 dfs 搜索树的过程，同样能保证每个桥梁边恰好经过两次，不改变奇偶性。这种 dfs 能保证在 \(t\) 时同时 dfs 找多个环的复杂度。
然后考虑偶实限制。这里我们做一个小限制：每次回溯时，从转折点出发找新的环，第一步必须是第奇数步，在找虚边。比如，上图中 \(a \rightsquigarrow u_2\) 和 \(b \rightsquigarrow u_3\) 的第一步都必须是第奇数步找虚边。而第一次到达 \(t\) 时，由于链长偶数，所以从 \(t\) 找环的第一步肯定是第奇数步。
另外，到达环上某个点时，因为这个环之前从来没走过，且环上的边都属于 \(S \oplus T\)，所以这个环上一条边实等价于这条边属于 \(S\)，一条边虚等价于这条边属于 \(T\)。到达环上任意一个点时，该点在环上的两条出边毗邻，所以一定有一条边属于 \(S\)，一条边属于 \(T\)，也即一定一虚一实。所以无论这一步是奇数步还是偶数步，下一步要走虚还是实，我们都有的走。
又因为环长是偶数，所以如果最后导向这个环的那条边是路径的第奇数步，也即这条边原先虚，现在变实，那么在经过环上偶数条边，再从这条边返回的时候，它一定是要走第偶数步，因为这条边已经变实了，所以满足偶实。然后一路回溯的时候，恰好也都能吻合，如下图。
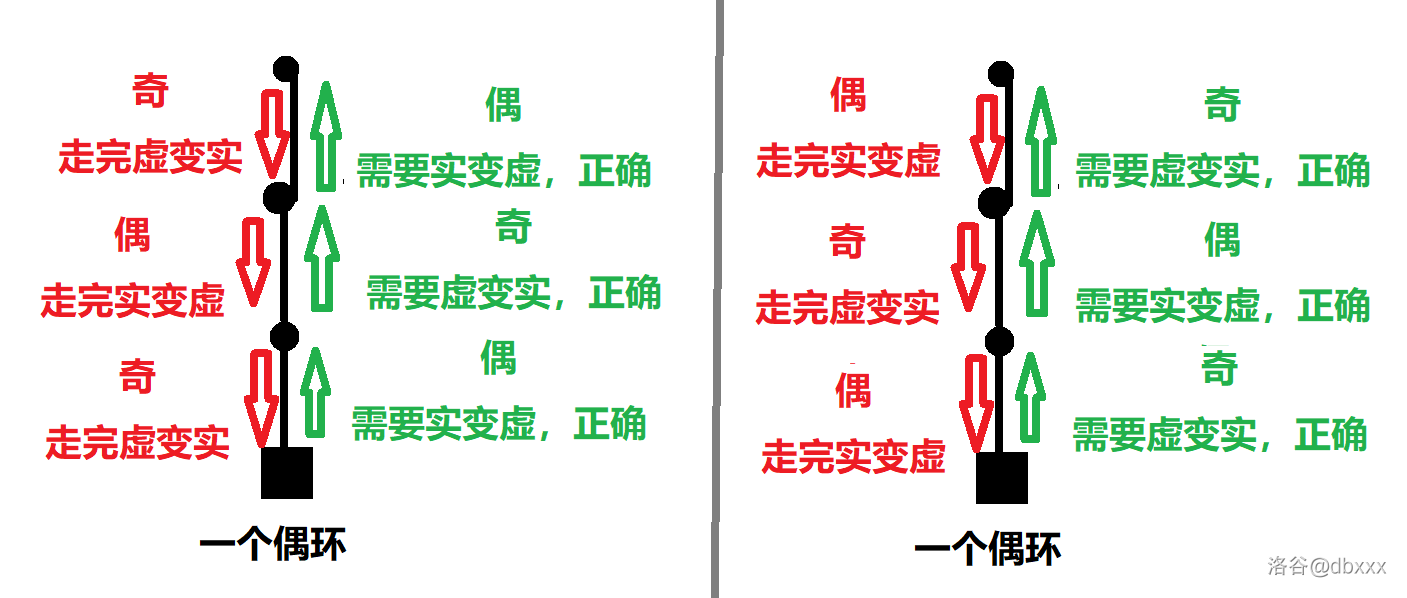
接下来就是最后一个问题了：为了保证任意一个环都能可达，需要保证从任意一个点出发，分别走虚边，实边，虚边……可达任意点。
证明我不会。参见一下 https://www.luogu.com.cn/discuss/621563 吧。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-06-26 23:05:05
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-06-26 23:05:05
*/
#include <bits/stdc++.h>
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
inline char rech() {
char ch = getchar();
while (!isgraph(ch))
ch = getchar();
return ch;
}
const int N = 2003, M = 2003;
struct edge {
int v;
char dir;
inline bool exi() {
return this -> v != 0;
}
};
edge S[N * M], T[N * M];
namespace all {
edge G[N * M][4]; // 0 1 2 3 代表四个方向
}
namespace dif {
edge G[N * M][2]; // 0 虚 1 实
}
int n, m;
inline int id(int x, int y) {
if (x < 1 || x > n || y < 1 || y > m)
return 0;
return (x - 1) * m + y;
}
std :: bitset <N * M> vis, key;
// key：是否是 S 和 T 的对称差图中，有边链接的点。以确定我们是否走到环上
inline void step(int &u) {
key.reset(u);
putchar(dif :: G[u][0].dir);
u = dif :: G[u][0].v;
key.reset(u);
u = dif :: G[u][1].v;
key.reset(u);
}
inline void go(int u, int st) {
while (u != st)
step(u);
}
void dfs(int u) {
vis.set(u);
for (int d = 0; d < 4; ++d) {
edge e = all :: G[u][d];
if (!e.exi())
continue;
int v = e.v; char dir = e.dir;
if (vis[v])
continue;
if (key[v]) {
int s = dif :: G[v][1].v, t = dif :: G[v][0].v;
// u -> v -> s -> ... -> t -> v -> u
putchar(dir);
go(s, t);
putchar(dif :: G[t][0].dir);
key.reset(v);
}
vis.set(v);
v = T[v].v;
if (!T[v].exi() || vis[v])
continue;
putchar(dir);
if (key[v]) {
int now = v;
step(now);
go(now, v);
}
else
dfs(v);
putchar(T[v].dir);
}
}
int main() {
n = read(); m = read();
auto ed = [](int u, char dir) -> edge {
int i = (u - 1) / m + 1, j = (u - 1) % m + 1;
switch (dir) {
case 'U': return (edge){id(i - 1, j), 'U'};
case 'D': return (edge){id(i + 1, j), 'D'};
case 'L': return (edge){id(i, j - 1), 'L'};
case 'R': return (edge){id(i, j + 1), 'R'};
}
return (edge){0, 'N'};
};
int s = 0, t = 0;
for (int k = 0; k <= 1; ++k) {
for (int u = 1; u <= n * m; ++u) {
edge e = {0, 'N'};
switch (rech()) {
case '<': e = ed(u, 'R'); break;
case '>': e = ed(u, 'L'); break;
case 'n': e = ed(u, 'D'); break;
case 'u': e = ed(u, 'U'); break;
}
if (k) {
T[u] = e;
if (!e.v)
t = u;
} else {
S[u] = e;
if (!e.v)
s = u;
}
}
}
for (int u = 1; u <= n * m; ++u) {
all :: G[u][0] = ed(u, 'U');
all :: G[u][1] = ed(u, 'D');
all :: G[u][2] = ed(u, 'L');
all :: G[u][3] = ed(u, 'R');
if (S[u].dir != T[u].dir && S[u].exi() && T[u].exi()) {
int s = S[u].v, t = T[u].v;
dif :: G[u][0] = T[u];
dif :: G[t][0] = T[t];
dif :: G[u][1] = S[u];
dif :: G[s][1] = S[s];
key[u] = key[s] = key[t] = 1;
}
}
vis.set(t);
go(s, t);
dfs(t);
return 0;
}
