P5025 SNOI2017 炸弹
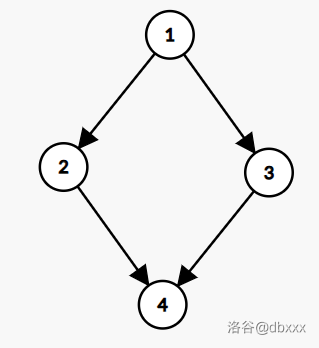
不难看出本题是可以转化为图论模型的：建立 \(n\) 个点代表 \(n\) 个炸弹，如果第 \(i\) 个炸弹能直接引爆第 \(j\) 个炸弹，就连边 \(i \to j\)。
这样的图论模型很好地刻画了原题中引爆的传递性，题意中第 \(i\) 个炸弹能直接 / 间接引爆第 \(j\) 个炸弹直接等价于图上 \(i\) 可达 \(j\)。问题变成，对于一个有向图，对每个点 \(u\) 求出 \(u\) 可达的点数。
这个问题可以被转化为对于一个 DAG，对每个点 \(u\) 求出 \(u\) 可达的点数（对原图缩点即可）。这个问题的强度相当于对每个点 \(u\) 求出 \(u\) 可达的点权和。
对 DAG 进行拓扑排序同时进行 dp，设 \(f(u)\) 表示点 \(u\) 的答案。我们设当前要求解 \(f(u)\)，其连向的点 \(v\) 的 \(f(v)\) 均已知（下称这些点为后继），试图写出转移方程。然而我们发现这个转移是难以做到的。
有一个想法是 \(f(u) = 1 + \sum f(v)\)。这种做法的错误原因在于，不同于树上 dp 中，一个点 \(u\) 的所有儿子的子树互不相交，DAG 上的 dp 里，点 \(u\) 的所有后继，它们的后代可能有交点。比如：
所以，直接将所有儿子的 \(f\) 相加会造成统计的重复。比如，点 \(2\) 可达 \(2\) 个点，点 \(3\) 可达 \(2\) 个点，按照上面的方程，会计算出点 \(1\) 可达 \(5\) 个点，明显错误。原因就是点 \(4\) 同时作为点 \(2\) 和点 \(3\) 的后代，累加时被统计了两次。
事实上，DAG 上统计点 \(u\) 可达点权和目前好像还没有人类会线性做法。然而，如果我们换个问题：DAG 上统计点 \(u\) 可达点权 \(\max\)，\(\min\)，\(\gcd\)……这些是可以简单 DAG dp 得到的，就像上面那样做就可以了。因为这些运算是可重复贡献的（即满足 \(x \operatorname{op} x = x\)），所以可以对点权重复统计。
但是本题要求我们统计点 \(u\) 可达点权和，这说明这个 DAG 应该是有一些特殊性质的，我们尝试找到。
不难发现，本题主动引爆一个炸弹后，所有被直接 / 间接引爆的炸弹构成包含主动被引爆炸弹的一段区间。这意味着，我们只需要找到引爆炸弹后，被直接 / 间接引爆的炸弹中，编号最小的那个和编号最大的那个，就可以计算出引爆炸弹的数量。
那么我们就可以将问题更换为寻找每个点 \(u\) 可达的点权 \(\max\) 和 \(\min\)。这是可以直接在 DAG 上 dp 的。
最后还有个事，就是本题暴力建边复杂度为 \(n^2\) 不可取，考虑线段树优化建图即可。
总结：笔者学习到了处理【在有向图上，对每个点 \(u\) 统计 \(u\) 可达的所有点的信息的合并】这种问题的方式。具体如下：
- 先考虑缩点，注意缩点时信息的合并。缩点之后变成 DAG，考虑 DAG 上 dp。
- 如果信息的合并方式不是可重复贡献的（比如权值和），则很可能不可做，否则（比如权值 \(\max\)，\(\min\)，\(\gcd\)）直接 dp 即可。
- 题目给出的信息要求我们计算每个点可达的权值和，可以先考虑转化成权值最值看看。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-06-21 19:39:54
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-06-21 20:55:17
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
inline int ls(int p) {
return p << 1;
}
inline int rs(int p) {
return p << 1 | 1;
}
inline bool gmi(int &a, int b) {
return b < a ? a = b, true : false;
}
inline bool gmx(int &a, int b) {
return b > a ? a = b, true : false;
}
const int N = (int)5e5 + 5;
int pos[N], rad[N], cnt;
struct node {
int l, r, x;
} t[N << 2];
namespace org {
std :: vector <int> G[N << 2];
}
namespace scc {
std :: vector <int> G[N << 2];
}
void build(int p, int l, int r) {
t[p].l = l;
t[p].r = r;
if (l == r) {
t[p].x = l;
return ;
}
t[p].x = ++cnt;
int mid = (l + r) >> 1;
build(ls(p), l, mid);
build(rs(p), mid + 1, r);
org :: G[t[p].x].push_back(t[ls(p)].x);
org :: G[t[p].x].push_back(t[rs(p)].x);
}
void connect(int p, int L, int R, int u) {
int l = t[p].l, r = t[p].r, x = t[p].x;
if (l == L && R == r)
return org :: G[u].push_back(x);
int mid = (l + r) >> 1;
if (R <= mid)
connect(ls(p), L, R, u);
else if (L > mid)
connect(rs(p), L, R, u);
else {
connect(ls(p), L, mid, u);
connect(rs(p), mid + 1, R, u);
}
}
int low[N << 2], dfn[N << 2], sccno[N << 2], times = 0;
int snt;
std :: stack <int> s;
void tarjan(int u) {
dfn[u] = low[u] = ++times;
s.push(u);
for (int v : org :: G[u]) {
if (!dfn[v]) {
tarjan(v);
gmi(low[u], low[v]);
} else if (!sccno[v])
gmi(low[u], dfn[v]);
}
if (low[u] == dfn[u]) {
++snt;
for (; ;) {
int x = s.top();
s.pop();
sccno[x] = snt;
if (x == u)
break;
}
}
}
int f[N << 2], g[N << 2];
int ind[N << 2];
void topsort(int n) {
std :: queue <int> q;
for (int u = 1; u <= n; ++u)
if (ind[u] == 0)
q.push(u);
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v : scc :: G[u]) {
--ind[v];
gmx(f[v], f[u]);
gmi(g[v], g[u]);
if (ind[v] == 0)
q.push(v);
}
}
}
signed main() {
int n = cnt = read();
for (int i = 1; i <= n; ++i) {
pos[i] = read();
rad[i] = read();
}
build(1, 1, n);
for (int i = 1; i <= n; ++i) {
int x = pos[i], d = rad[i];
int l = std :: lower_bound(pos + 1, pos + 1 + n, x - d) - pos;
int r = std :: upper_bound(pos + 1, pos + 1 + n, x + d) - pos - 1;
connect(1, l, r, i);
}
for (int u = 1; u <= (n << 2); ++u)
if (!dfn[u])
tarjan(u);
std :: memset(g, 0x3f, sizeof(g));
for (int u = 1; u <= n; ++u)
f[sccno[u]] = u;
for (int u = n; u; --u)
g[sccno[u]] = u;
for (int u = 1; u <= (n << 2); ++u)
for (int v : org :: G[u])
if (sccno[u] != sccno[v]) {
scc :: G[sccno[v]].push_back(sccno[u]);
++ind[sccno[u]];
}
topsort(n << 2);
int ans = 0;
const int mod = (int)1e9 + 7;
for (int u = 1; u <= n; ++u)
(ans += u * (f[sccno[u]] - g[sccno[u]] + 1)) %= mod;
printf("%lld\n", ans);
return 0;
}
