P3960 NOIP2017 提高组 列队
P3960 NOIP2017 提高组 列队 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这个队伍的人数最多是全球人口的 15 倍。
慢慢开部分分。这题部分分给的相当足。
30 pts：1~6
\((n + m)q\) 暴力即可。
50 pts：7~10
其实 \((n + m)q\) 时间复杂度仍然可以通过，但空间复杂度 \(nm\) 是不可过的。
遍历一遍所需的空间，时间复杂度就会和空间复杂度同阶，而这里时间复杂度却远低于空间复杂度，说明肯定有大量空间是赘余的。
观察到 \(q \le 500\)，最多只会删除 \(500\) 个点，不难发现除了这 \(500\) 个点所在的行和最后一列上的点以外，其它的点从始至终位置不变，更不可能出现在答案中。
因此只需要把这 \(500\) 行上的点所在行数离散化后存入数组后再暴力即可。空间复杂度 \(mq\)。
80 pts：11~16
核心条件是 \(x = 1\)。容易发现只有第一行和最后一列上的点在变化，其他的点始终不动，不可能出现在答案中，直接忽略即可。
其实 \((1, 1), (1, 2), \cdots, (1, m), (2, m), \cdots (n, m)\) 就是一个支持取出第 \(k\) 个元素并置于队尾的队列，只是从中间掰成了直角罢了。
每次取出第 \(k\) 个元素，想到类似于约瑟夫问题的树状数组做法。
我们开辟出一个大小为 \(n + m - 1 + q\) 的数组 \(t\)，前 \(n + m - 1\) 个元素值为 \(1\)，代表这个土地有人；后 \(q\) 个元素值为 \(0\)，代表这个空地无人。删除第 \(k\) 个元素时，其实也就是找前缀和为 \(k\) 的土地编号（代表这里以及前面恰好有 \(k\) 个人），然后把这个位置的 \(1\) 改成 \(0\)，代表这里的人没了。于是删除一个人后面的人是不用动位置的。然后把这个人丢在最后一个人后面那个空地上就行了，即把那个空地的 \(0\) 改成 \(1\)。\(t\) 使用树状数组加速即可。
和约瑟夫问题不同，这个题的空地编号不一定是队列中人的编号。开个和 \(t\) 大小一样的数组记录空地编号对应的人的编号就可以了。
80 pts 代码
/*
* @Author: crab-in-the-northeast
* @Date: 2022-10-26 15:16:43
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2022-10-26 18:15:23
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool flag = true;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-')
flag = false;
ch = getchar();
}
while (isdigit(ch)) {
x = (x << 1) + (x << 3) + ch - '0';
ch = getchar();
}
if(flag)
return x;
return ~(x - 1);
}
inline int lowbit(int x) {
return x & (-x);
}
const int maxn = (int)3e5 + 5;
const int maxm = (int)3e5 + 5;
const int maxq = (int)3e5 + 5;
int qx[maxq], qy[maxq];
int bit[maxn + maxm + maxq];
int no[maxn + maxm + maxq];
int li;
inline void del(int x) {
for (; x <= li; x += lowbit(x))
--bit[x];
}
inline int kth(int k) {
int ans = 0, sum = 0;
for (int i = 20; ~i; --i) {
ans += (1 << i);
if (ans > li || sum + bit[ans] >= k)
ans -= (1 << i);
else
sum += bit[ans];
}
return ans + 1;
}
int ux[maxq];
int a[505][maxm];
int col[maxn];
signed main() {
int n = read(), m = read(), q = read();
bool pure = true;
for (int i = 1; i <= q; ++i) {
int x = read(), y = read();
qx[i] = x;
qy[i] = y;
if (x != 1)
pure = false;
}
if (pure) {
li = n + m + q;
for (int i = 1; i <= n + m + q; ++i)
bit[i] = lowbit(i);
int lst = m + n - 1;
for (int i = 1; i <= m; ++i)
no[i] = i;
for (int i = 2; i <= n; ++i)
no[m + i - 1] = m * i;
for (int i = 1; i <= q; ++i) {
int y = qy[i];
int x = kth(y);
printf("%lld\n", no[x]);
del(x);
no[++lst] = no[x];
}
} else {
std :: copy(qx + 1, qx + q + 1, ux + 1);
std :: sort(ux + 1, ux + q + 1);
int *en = std :: unique(ux + 1, ux + q + 1);
for (int i = 1; i <= q; ++i) {
int x = qx[i];
int dix = std :: lower_bound(ux + 1, en, qx[i]) - ux;
for (int j = 1; j < m; ++j)
a[dix][j] = (x - 1) * m + j;
}
for (int i = 1; i <= n; ++i)
col[i] = i * m;
for (int i = 1; i <= q; ++i) {
int x = qx[i], y = qy[i];
int dix = std :: lower_bound(ux + 1, en, qx[i]) - ux;
if (y < m) {
int num = a[dix][y];
printf("%lld\n", num);
for (int j = y; j < m - 1; ++j)
a[dix][j] = a[dix][j + 1];
a[dix][m - 1] = col[x];
for (int j = x; j < n; ++j)
col[j] = col[j + 1];
col[n] = num;
} else {
int num = col[x];
printf("%lld\n", num);
for (int j = x; j < n; ++j)
col[j] = col[j + 1];
col[n] = num;
}
}
}
return 0;
}
100pts：17~20
80pts 到 100pts 这一步的思维跨度远比 0pts 到 80pts 这步大。考场上请务必拿到 80 pts，非常可观。
不过据说 100pts 可以通过使用更高级的数据结构而少走思维弯路。
我们刚刚成功维护了一个数据结构（队列），满足：
- 找到第 \(k\) 个元素并删除；
- 在结尾插入一个元素。
再仔细思考，我们会发现：这个矩阵的去除最后一个元素的每一行和最后一列，总共 \(n + 1\) 个队列其实本质都是这样的一个数据结构。也就是我们可以把矩阵划分成这样：
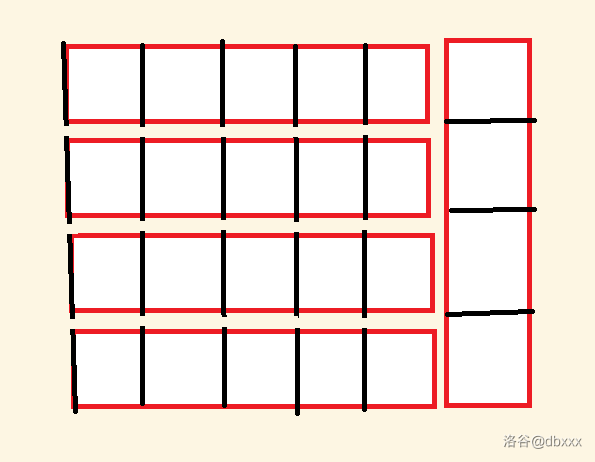
一个红色的矩形就表示一个队列。
查询 \((x, y)\) 的时候，除非 \(y = m\)，否则都是第 \(x\) 个横向队列和纵向队列之间配合完成操作。而 \(y = m\) 时，只需要考虑纵向队列的操作。
具体配合是以下两段的对接：第 \(x\) 个横向队列，和纵向队列从第 \(x\) 个元素开始的一个后缀。
但是，由于空间限制，我们无法开 \(n +1\) 个树状数组实现这个过程。
发现处在不同行数的元素的离队顺序，对于横向队列而言，是相互独立互不影响的（如果暂时不考虑和纵向队列对接），只有处在同一行的元素离队会因为处在同一行而互相影响。
因此想到将询问离线，按照所在行数分类。对于所有的横向队列，我们共用一个树状数组：先把第一行的所有信息在这个树状数组处理好，再把这个树状数组复原为初始状态（全为 \(1\)），再处理第二行的所有信息，再复原……
复原暴力显然是不行的。我们考虑在修改时，用一个 vector 记录把哪些元素从 \(1\) 修改为 \(0\) 了，那么复原时只需复原这些被修改的元素为 \(1\) 即可。
但是有一点：不同行数元素离队顺序在对接前，对于横向队列不影响，但对接后，会影响纵向队列，也可能进而影响横向队列（因为纵向队列中的元素会跑到横向队列）。比如：\((2, 2)\) 先离队，\((1, 1)\) 后离队和 \((1, 1)\) 先离队，\((2, 2)\) 后离队两种情况是不同的。所以我们不能将询问离线排序之后，直接模拟对接这个过程。
询问离线排序了，还不能直接模拟对接。那么考虑先运用树状数组预处理信息，然后再运用这些信息，按照题目给出的离队顺序，模拟整个矩阵上的离队和对接。
显然同一行内的离队信息应该按照离队的时间顺序（即输入顺序）处理。
对于 \(x\) 这一行，如果有一次离队操作 \((x, i)\)，我们分两种情况讨论：
- \(i = m\)，事实上这次离队不在第 \(x\) 个横向队列中，只在纵向队列中做出影响；我们作出特殊标记。
- \(i < m\)，说明这次离队在第 \(x\) 个横向队列中。我们取出树状数组中第 \(i\) 个元素（输出并删除）。在树状数组中，对应了前缀和为 \(i\) 对应的那个土地编号 \(j\)。我们将 \(j\) 记入这次离队的信息。
\(j\) 的含义比较难用语言解释，可以先接着往下看，并配合 80pts 做法中的土地编号这一概念思考。
80 pts 中空地编号对应人编号的数组显然也是需要优化的。我们使用动态 vector，并且不存储 \(j \le m\) 的情况（因为此时人编号可以根据 \((x - 1) \times m + j\) 直接算出）。这样，所有 vector 存储的多余的编号最多达到 \(q\) 的量级，可以通过本题。
这两段有点难以理解（我自己都觉得），读不懂没关系，建议阅读代码！
/*
* @Author: crab-in-the-northeast
* @Date: 2022-10-27 16:07:43
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2022-10-27 17:09:25
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool flag = true;
char ch = getchar();
while (!isdigit(ch)) {
if (ch == '-')
flag = false;
ch = getchar();
}
while (isdigit(ch)) {
x = (x << 1) + (x << 3) + ch - '0';
ch = getchar();
}
if(flag)
return x;
return ~(x - 1);
}
inline int lowbit(int x) {
return x & (-x);
}
const int maxn = (int)3e5 + 5;
const int maxm = (int)3e5 + 5;
const int maxq = (int)3e5 + 5;
struct fenwick {
int lim;
int bit[maxn + maxm + maxq];
inline void add(int x, int v) {
for (; x <= lim; x += lowbit(x))
bit[x] += v;
}
inline int kth(int k) {
int ans = 0, sum = 0;
for (int i = 20; ~i; --i) {
ans += (1 << i);
if (ans > lim || sum + bit[ans] >= k)
ans -= (1 << i);
else
sum += bit[ans];
}
return ans + 1;
}
} ve, ho;
typedef std :: pair <int, int> pii;
pii qts[maxq];
bool ism[maxq];
std :: vector <int> qt[maxn];
std :: vector <int> mdy;
std :: vector <int> veno[maxn];
std :: vector <int> homo;
// veno 类似于 80pts 做法中的 no 数组（但有改动），对横向队列而言
// homo 也类似于 no 数组，对竖向队列而言，有微改动（不多）
signed main() {
int n = read(), m = read(), q = read();
ve.lim = m + q;
ho.lim = n + q;
for (int i = 1; i <= ve.lim; ++i)
ve.bit[i] = lowbit(i);
for (int i = 1; i <= ho.lim; ++i)
ho.bit[i] = lowbit(i);
homo.push_back(0);
for (int i = 1; i <= n; ++i)
homo.push_back(i * m);
for (int i = 1; i <= q; ++i) {
int x = read(), y = read();
if (y == m)
ism[i] = true;
qts[i] = std :: make_pair(x, y);
qt[x].push_back(i);
}
for (int x = 1; x <= n; ++x) {
for (auto id : qt[x]) {
if (ism[id])
continue;
int y = qts[id].second;
y = ve.kth(y);
ve.add(y, -1);
mdy.push_back(y);
qts[id].second = y;
}
for (int y : mdy)
ve.add(y, 1);
mdy.clear();
}
for (int i = 1; i <= q; ++i) {
int x = qts[i].first, y = qts[i].second;
int num = 0;
if (!ism[i]) {
if (y < m)
num = (x - 1) * m + y;
else
num = veno[x][y - m];
}
int coy = ho.kth(x);
ho.add(coy, -1);
int nw = homo[coy];
if (ism[i])
num = nw;
else
veno[x].push_back(nw);
printf("%lld\n", num);
homo.push_back(num);
}
return 0;
}
