[luogu p2282] 组合数问题
组合数问题
题目描述
组合数 \(\binom{n}{m}\) 表示的是从 \(n\) 个物品中选出 \(m\) 个物品的方案数。举个例子,从 \((1,2,3)\) 三个物品中选择两个物品可以有 \((1,2),(1,3),(2,3)\) 这三种选择方法。根据组合数的定义,我们可以给出计算组合数 \(\binom{n}{m}\) 的一般公式:
其中 \(n!=1\times2\times\cdots\times n\);特别地,定义 \(0!=1\)。
小葱想知道如果给定 \(n,m\) 和 \(k\),对于所有的 \(0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )\) 有多少对 \((i,j)\) 满足 \(k|\binom{i}{j}\)。
输入输出格式
输入格式
第一行有两个整数 \(t,k\),其中 \(t\) 代表该测试点总共有多少组测试数据,\(k\) 的意义见问题描述。
接下来 \(t\) 行每行两个整数 \(n,m\),其中 \(n,m\) 的意义见问题描述。
输出格式
共 \(t\) 行,每行一个整数代表所有的 \(0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )\) 中有多少对 \((i,j)\) 满足 \(k|\binom{i}{j}\)。
输入输出样例
输入样例 #1
1 2
3 3
输出样例 #1
1
输入样例 #2
2 5
4 5
6 7
输出样例 #2
0
7
说明
【样例1说明】
在所有可能的情况中,只有 \(\binom{2}{1} = 2\) 一种情况是 \(2\) 的倍数。
【子任务】
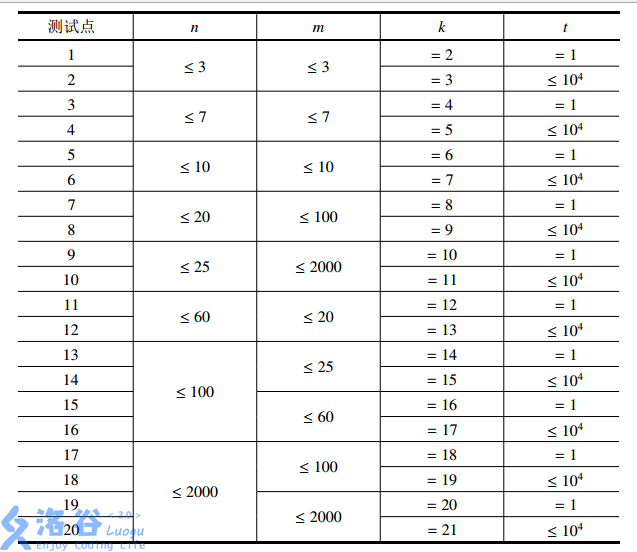
- 对于全部的测试点,保证 \(0 \leq n, m \leq 2 \times 10^3\),\(1 \leq t \leq 10^4\)。
分析
这题一看就要用 \(\operatorname{O}(n ^ 2)\) 预处理 \(\operatorname{O}(1)\) 回答的算法,那么具体怎么做呢?
首先用杨辉三角预处理出2000内所有的组合数对 \(k\) 取模的结果。如下:
void init(int k) {
c[0][0] = c[1][0] = c[1][1] = 1;
for (int i = 2; i < maxn; ++i) {
c[i][0] = 1;
for (int j = 1; j <= i; ++j) {
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % k;
}
}
}
然后仔细观察题目要求什么:
对于所有的 \(0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )\) 有多少对 \((i,j)\) 满足 \(k|\binom{i}{j}\)。
为了方便讨论,若 \(m > n\),我们一律令 \(n \rightarrow m\)。
定义 \(ans_{i, j}\) 为答案数组,用二维前缀和得到公式:
当然,如果我们发现 \(k|\binom{i}{j}\),那么 \(ans_{i, j}\) 还需自增 \(1\)。
我们就可以写出这样的代码:
void init(int k) {
c[0][0] = c[1][0] = c[1][1] = 1;
for (int i = 2; i < maxn; ++i) {
c[i][0] = 1;
for (int j = 1; j <= i; ++j) {
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % k;
ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1];
if (c[i][j] == 0) ++ans[i][j];
}
}
}
然而就这样结束了吗?
如果这样,提交程序,你会发现你的代码能拿到15分的好成绩。
这是为什么呢?
不妨来看看当 \(k = 5\) 时,ans的表如何。(此处列举了前10*10个)
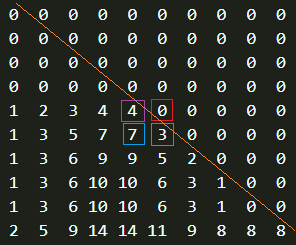
显然,绿色方块的值是红+蓝-紫。但是你发现没有,红色方块的所在位置已经超出了杨辉三角的预处理范围。(橙色左下方为预处理范围,右上角为非预处理范围),也就是当 \(i = j\) 时,\(ans_{i - 1, j}\) 没有被处理。
但是,这个东西其实很好处理,因为 \(ans_{i+1, i} = ans_{i, i}\)。至于这是为什么,见其定义:
对于所有的 \(0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )\) 有多少对 \((i,j)\) 满足 \(k|\binom{i}{j}\)。
观察到这个 \(min(i, m)\) 了吗?这个的意思就是说,当 \(m > n\) 时,\(ans_{m, n}\) 和 \(ans _{n, n}\) 其实是等价的。
同样的道理便可以得到 \(ans_{i+1, i} = ans_{i, i}\)。因此只要在i循环中最后加一句ans[i][i + 1] = ans[i][i];即可。代码如下:
void init(int k) {
c[0][0] = c[1][0] = c[1][1] = 1;
for (int i = 2; i < maxn; ++i) {
c[i][0] = 1;
for (int j = 1; j <= i; ++j) {
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % k;
ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1];
if (c[i][j] == 0) ++ans[i][j];
}
ans[i][i + 1] = ans[i][i];
}
}
这样就可以AC啦~上一个整体代码吧!
代码
/*
* @Author: crab-in-the-northeast
* @Date: 2020-10-01 14:01:33
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-10-01 16:18:48
*/
#include <iostream>
#include <cstdio>
const int maxn = 2005;
const int maxm = 2005;
long long c[maxn][maxm], ans[maxn][maxm];
void init(int k) {
c[0][0] = c[1][0] = c[1][1] = 1;
for (int i = 2; i < maxn; ++i) {
c[i][0] = 1;
for (int j = 1; j <= i; ++j) {
c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % k;
ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1];
if (c[i][j] == 0) ++ans[i][j];
}
ans[i][i + 1] = ans[i][i];
}
}
int main() {
int t, k;
std :: scanf("%d %d", &t, &k);
init(k);
while (t--) {
int n, m;
std :: scanf("%d %d", &n, &m);
std :: printf("%lld\n", ans[n][m > n ? n : m]);
}
return 0;
}


