[luogu p1884] [USACO12FEB]Overplanting S
在笛卡尔直角坐标系中,给定若干个四边均与坐标轴平行的矩形,求覆盖到的面积。
这个题目就是求所有矩形的面积并。
考虑这样一种矩形切割的做法:每到一个矩形
什么意思呢,举一个例子吧。
我之前有一个矩形
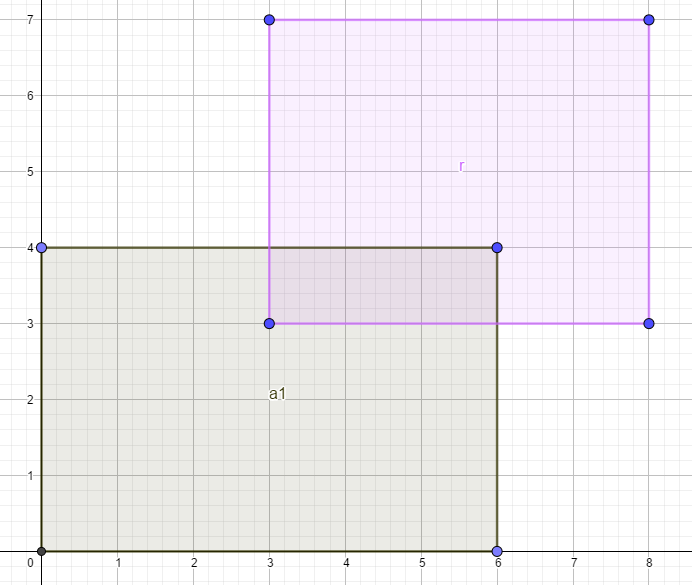
我们用
可以看到,
此时,一个新矩形
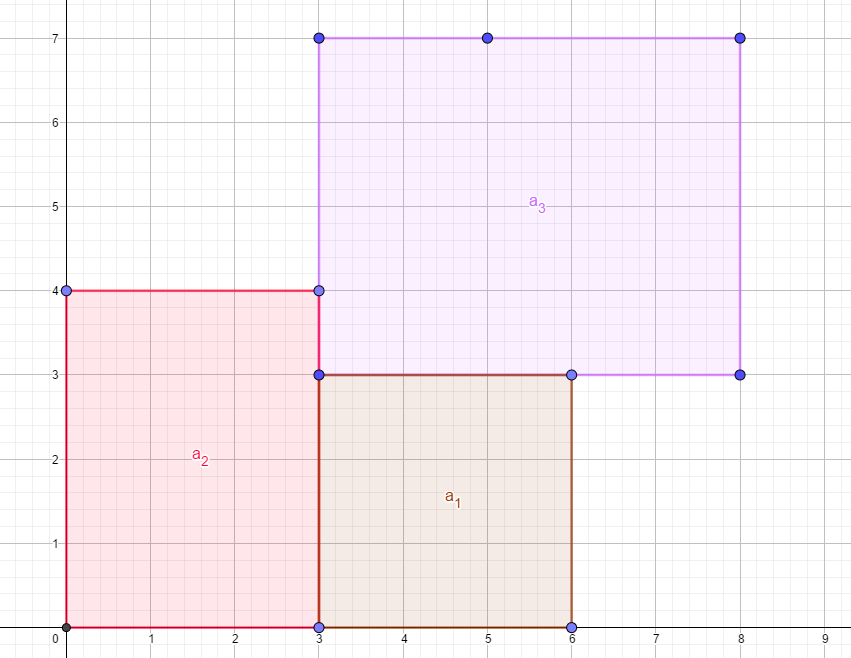
这个
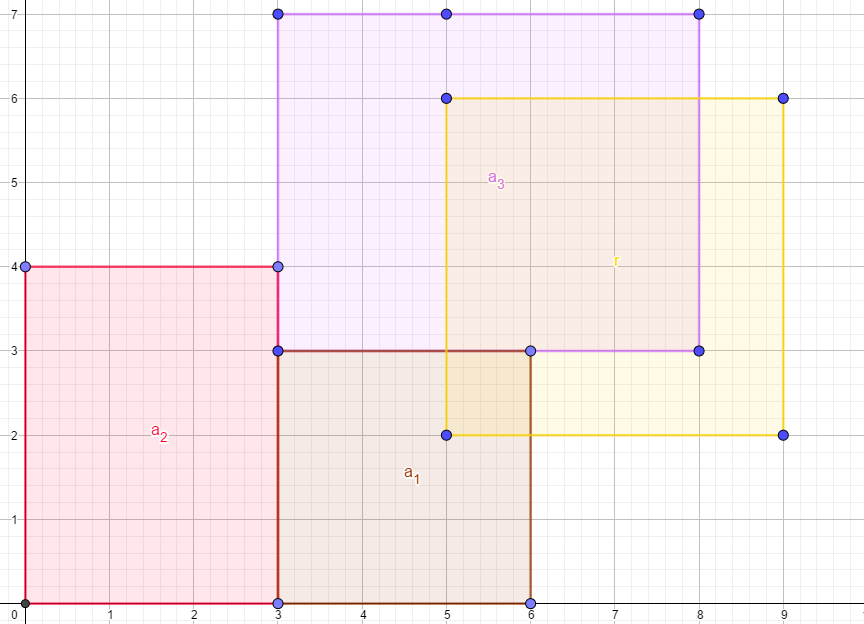
先切
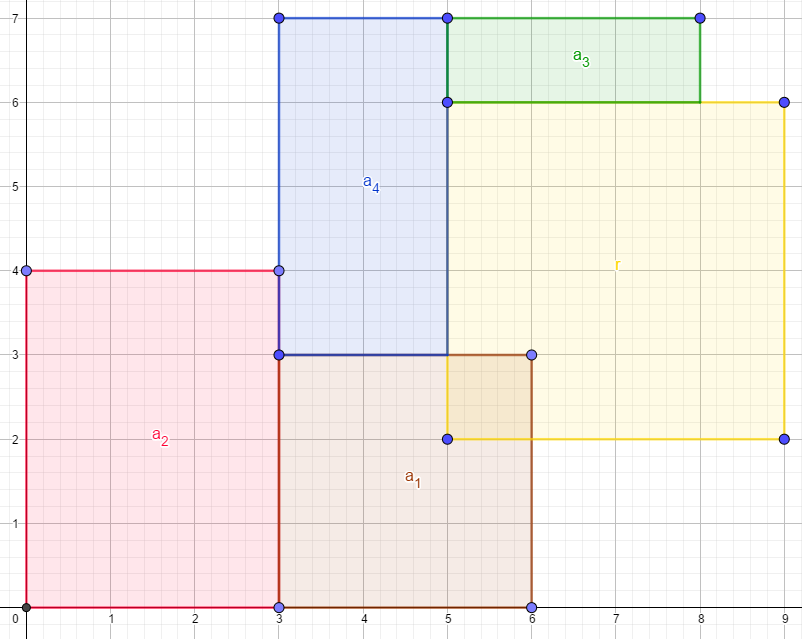
再切
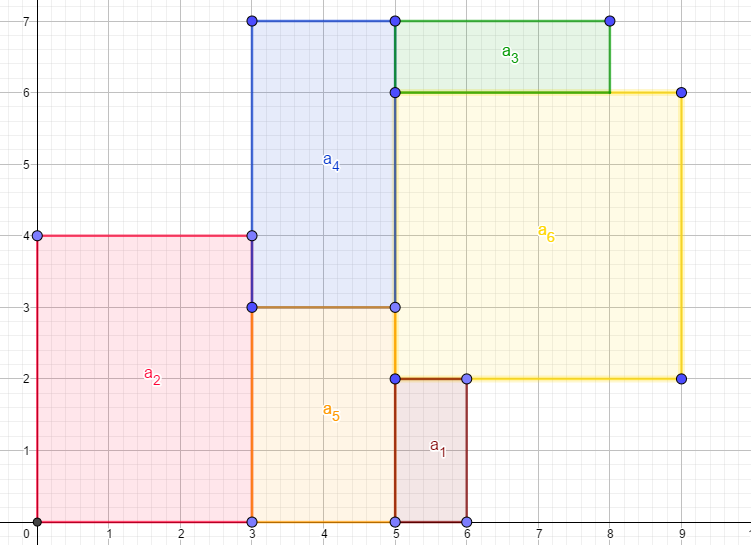
最后,计算每个矩形的面积即可。
思路明朗,代码实现就不难了。
矩形切割的cut函数如下:
void cut(int id, int x1, int y1, int x2, int y2) {
long long k1, k2, k3, k4;
k1 = max(a[id].x1, x1);
k2 = min(a[id].x2, x2);
k3 = min(a[id].y1, y1);
k4 = max(a[id].y2, y2);
if (a[id].x1 < k1) a[++cnt] = (rectangle){a[id].x1, a[id].y1, k1, a[id].y2};
if (a[id].x2 > k2) a[++cnt] = (rectangle){k2, a[id].y1, a[id].x2, a[id].y2};
if (a[id].y1 > k3) a[++cnt] = (rectangle){k1, a[id].y1, k2, k3};
if (a[id].y2 < k4) a[++cnt] = (rectangle){k1, k4, k2, a[id].y2};
}
/*
* @Author: crab-in-the-northeast
* @Date: 2020-10-31 10:57:53
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-10-31 10:57:53
*/
#include <iostream>
#include <cstdio>
const int maxn = 1005;
inline long long max(long long a, long long b) {
return a > b ? a : b;
}
inline long long min(long long a, long long b) {
return a < b ? a : b;
}
struct rectangle {
long long x1, y1;
long long x2, y2;
}a[maxn];
int cnt = 0;
void cut(int id, int x1, int y1, int x2, int y2) {
long long k1, k2, k3, k4;
k1 = max(a[id].x1, x1);
k2 = min(a[id].x2, x2);
k3 = min(a[id].y1, y1);
k4 = max(a[id].y2, y2);
if (a[id].x1 < k1) a[++cnt] = (rectangle){a[id].x1, a[id].y1, k1, a[id].y2};
if (a[id].x2 > k2) a[++cnt] = (rectangle){k2, a[id].y1, a[id].x2, a[id].y2};
if (a[id].y1 > k3) a[++cnt] = (rectangle){k1, a[id].y1, k2, k3};
if (a[id].y2 < k4) a[++cnt] = (rectangle){k1, k4, k2, a[id].y2};
}
int main() {
int n;
std :: scanf("%d", &n);
long long x1, y1, x2, y2;
std :: scanf("%lld %lld %lld %lld", &x1, &y1, &x2, &y2);
a[++cnt] = (rectangle){x1, y1, x2, y2};
for (int i = 2; i <= n; ++i) {
std :: scanf("%lld %lld %lld %lld", &x1, &y1, &x2, &y2);
for (int j = 1; j <= cnt; ++j) {
if (a[j].x1 < x2 && a[j].x2 > x1 && a[j].y1 > y2 && a[j].y2 < y1) {
cut(j, x1, y1, x2, y2);
a[j--] = a[cnt--];
}
}
a[++cnt] = (rectangle){x1, y1, x2, y2};
}
long long ans = 0;
for (int i = 1; i <= cnt; ++i)
ans += (a[i].x2 - a[i].x1) * (a[i].y1 - a[i].y2);
std :: printf("%lld\n", ans);
return 0;
}
如果使用容斥原理,一个地方可能重复不止两次,所以有可能会算乱。
为了避免这种情况,我们便采用矩形切割这种做法。
好做不乱。
据说本题还可以用线段树+离散化,但是想想就麻烦。。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】