[luogu p1364] 医院设置 & 找树的重心 学习笔记
医院设置
题目描述
设有一棵二叉树,如图:
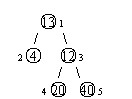
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 \(1\)。如上图中,若医院建在1 处,则距离和 \(=4+12+2\times20+2\times40=136\);若医院建在 \(3\) 处,则距离和 \(=4\times2+13+20+40=81\)。
输入输出格式
输入格式
第一行一个整数 \(n\),表示树的结点数。
接下来的 \(n\) 行每行描述了一个结点的状况,包含三个整数 \(w, u, v\),其中 \(w\) 为居民人口数,\(u\) 为左链接(为 \(0\) 表示无链接),\(v\) 为右链接(为 \(0\) 表示无链接)。
输出格式
一个整数,表示最小距离和。
输入输出样例
输入样例 #1
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
输出样例 #1
81
说明
数据规模与约定
对于 \(100\%\) 的数据,保证 \(1 \leq n \leq 100\),\(0 \leq u, v \leq n\),\(1 \leq w \leq 10^5\)。
分析
此题\(n \leq 100\),所以可以用floyd直接水过。
但直接用floyd的话,这道题还有什么挑战性?
于是我仔细分析了一下这道题,这道题是求树的重心。
求树的重心有没有什么巧妙的办法呢?
想了1145141919810年后,没想出来。
于是我毫不犹豫打开了题解,于是就看到了题解区的第一篇题解,终于学会了求树的重心。
看完\(\operatorname{O}(n)\)的做法后,我的脑海中只剩下了一个词: Orz
现在我就来记录一下自己学到的在树中找重心的方法。
首先,邻接表存图,然后dfs,预处理出所有节点的大小。(大小定义为此点的权值+所有儿子的大小)
伪代码如下:
void dfs(int u, int father, int depth) {
siz[u] = w[u];
for (int i = head[u]; i; i = edge[i].nxt)
if (edge[i].v != father) {
dfs(edge[i].v, u, depth + 1);
siz[u] += siz[edge[i].v];
}
dp[1] += w[u] * depth;
}
此处:
- w代表此点权值,也就是题目中的w
- siz代表此点大小
- dp代表以此点为根的总距离
然后就是dp环节。
首先既然是dp,那么状态转移方程是什么呢?
先说状态转移方程:
为什么?
首先先从变化的角度来看这个问题。
重心从父节点\(u\)转到子节点\(v\),显然,\(v\)的子树中所有的单位权值(注意不是所有的子节点哦。子节点是一个地方,在此题代表社区。单位权值在此题就代表人)到重心(此题代表医院)的距离都会少\(1\)。这点应该不难理解吧?这样总距离就会少\(siz_v\)。
但是这样的代价是什么呢?不是\(v\)的子树中单位权值的,到重心的距离就会多\(1\)。这样总距离就会增加\(siz_1 - siz_v\)。于是状态转移方程得证。
而答案,就是这些dp值中最小的那个。
dp环节伪代码:
void work(int u, int father) {
for (int i = head[u]; i; i = edge[i].nxt)
if (edge[i].v != father) {
dp[edge[i].v] = dp[u] - siz[edge[i].v] * 2 + siz[1];
work(edge[i].v, u);
}
ans = ans < dp[u] ? ans : dp[u];
}
两个重要的核心说完了,其他都是细枝末节了,所以其实此处不上代码你应该也能自己写出来了。
好,上代码。
dbxxx,你不是说此处不上代码,别人也能写出来吗?那你为啥还上?
你咋那么多事,别管了,上就完事了
代码
/*
* @Author: crab-in-the-northeast
* @Date: 2020-08-01 22:01:07
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-08-02 16:58:35
*/
//找树的重心,学习于P1364第一篇题解。
#include <iostream>
#include <cstdio>
#include <climits>
const int maxn = 105;
struct Edge {
int v, nxt;
}edge[maxn << 1];
int w[maxn];
int head[maxn], idx, n, siz[maxn];
int ans = INT_MAX >> 2, dp[maxn];
inline void addEdge(int u, int v) {
edge[++idx].v = v;
edge[idx].nxt = head[u];
head[u] = idx;
}
void dfs(int u, int father, int depth) {
siz[u] = w[u];
for (int i = head[u]; i; i = edge[i].nxt)
if (edge[i].v != father) {
dfs(edge[i].v, u, depth + 1);
siz[u] += siz[edge[i].v];
}
dp[1] += w[u] * depth;
}
void work(int u, int father) {
for (int i = head[u]; i; i = edge[i].nxt)
if (edge[i].v != father) {
dp[edge[i].v] = dp[u] - siz[edge[i].v] * 2 + siz[1];
work(edge[i].v, u);
}
ans = ans < dp[u] ? ans : dp[u];
}
int main(){
std :: scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
std :: scanf("%d", &w[i]);
int a, b;
std :: scanf("%d%d", &a, &b);
if (a) {
addEdge(a, i);
addEdge(i, a);
}
if (b) {
addEdge(b, i);
addEdge(i, b);
}
}
dfs(1, 0, 0);
work(1, 0);
printf("%d", ans);
return 0;
}

