本文中,设树中所有权都是正的。
直径的定义:不经过同一个点两次的最长链。
中心的定义:对于点 u,如果满足所有点到点 u 距离的最大值最小,则点 u 是中心。
请注意树的中心和树的重心是两个不同的概念。
本文中 u∼v 代表树上 u↭v 唯一路径的权值。
性质一
如果一个点 u 在一条直径 D 上,D 的端点是 s 和 t,那么 u↭s 和 u↭t 中较长的一定是一条从 u 出发的最长链。
假设存在一条链 u↭w 比 u↭s 和 u↭t 都长。
因为 s,u,t 依次位于一条链上(直径显然是链),
所以 u↭w 如果和 u↭s 有交点,就一定和 u↭t 无交点(否则会出现环)。
如果 u↭w 与 u↭s 没有交点,那么 s↭u↭w 才应该是直径。
如果 u↭w 与 u↭t 没有交点,那么 t↭u↭w 才应该是直径。
反正无论如何都和 D 是直径矛盾。命题成立。
性质二
从任意一个点出发,能到达的最远点一定是某条直径的端点。
下面这个图中,我们从 x 找到最远的点 y,并设原树直径为 m↭n。

性质三
直径的端点一定都是叶子节点。
如果直径的端点不是叶子节点,即有两个出度及以上,那么直径这条链只会占用一个出度,一定可以从另一个出度继续走下去从而达到更长的链。
性质四
用一条边 (u,v) 将两棵树 T1,T2 连接,合成的新树 T 的所有直径都只有两种情况:
- 不经过 (u,v),仍为原来 T1 的某条直径,或仍为原来 T2 的某条直径。
- 经过 (u,v),两个端点分别落在 T1 和 T2 中,且分别是 T1,T2 中某条直径的某个端点。
不经过 (u,v),即新直径只能在 T1 或 T2 中走,很明显它必须是 T1 的一条直径或 T2 的一条直径。
经过 (u,v),则设新直径为 s↭u⟷v↭t。
不妨设 s↭u 这段在 T1 中,v↭t 这段在 T2 中。为符合直径定义,我们期望最大化 s↭u 和 v↭t。
为此,必须在 T1 中找一个离 u 最远的某个点作为 s,在 T2 中找一个离 v 最远的点作为 t。
根据之前的性质,s 肯定是 T1 中某条直径的端点;t 肯定是 T2 中某条直径的端点,证毕。
性质五
一棵树上,一定存在一个点 p 被这棵树的所有直径经过。
假设树存在两根不相交的直径 a↭b 和 c↭d。直径长度相同,(a∼b)=(c∼d)。
因为树的结构,所以 a↭b 上一定存在一个点 p,c↭d 上一定存在一个点 q,满足 p 和 q 连通且 p↭q 和 a↭b 和 c↭d 都不相交。
不妨设 (a∼p)≥(b∼p)(否则交换一下 a 和 b 就好了),(c∼q)≥(d∼q)(同理)。
那么 (a∼p)≥21(a∼b),(c∼q)≥21(c∼d)=21(a∼b),所以 (a∼p)+(c∼q)≥(a∼b)。
因为边权是正的,所以 (p∼q)>0,因此有 (a∼p)+(p∼q)+(q∼c)>(a∼b)。
因此 a↭b 不是直径,与题设矛盾。
因此任意两条直径都存在一个交点。
由于是树,所以三条直径两两相交不交于同一点这种情况不可能成立(会成环)。所以只能多条直径同时交于一个点,证毕。
性质六
任意两条直径一定有且仅有一个极长连续段(可以只是一个点)重合。若两条直径共用一个端点,这个端点也算重合。
首先任意两条直径之间一定有交点,一个点也是一个连续段,所以一定会有一个连续段重合。
其次如果有两个极长重合连续段,如下(a↭b 和 c↭d 为两条直径):
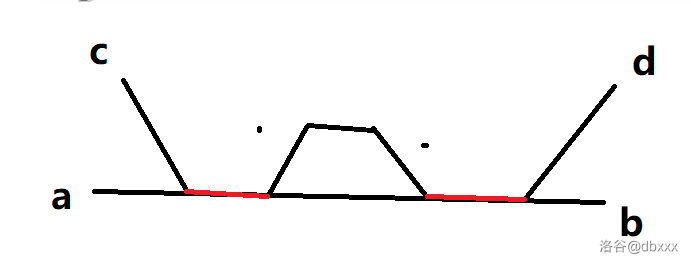
会出现环,这是树上不能出现的。
所以任意两条直径其实只有两种形态:X 形态和 Y 形态。
X 形态:两条直径的四个端点都互异,如下(a↭b 和 c↭d 为两条直径):
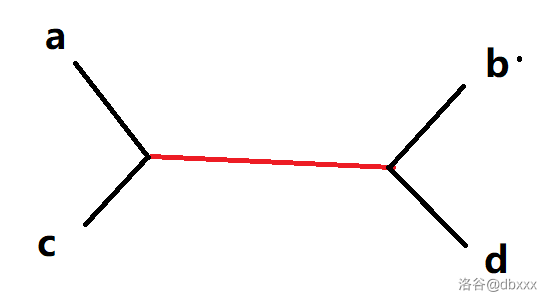
Y 形态:两条直径共用一个端点,如下(a↭b 和 a↭c 为两条直径)。
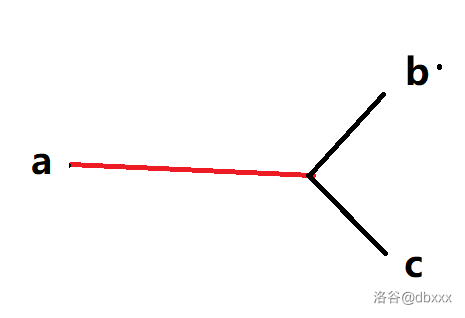
啥,你问能不能共用俩端点?那就成完全重合的两条直径了,看成一条就行了。
性质七
对于树上任意两条直径,从中间重合段的任意一个端点出发,引申出来的直径剩余的部分长度相同。
上述表述有点抽象。解释一下。a↭b 和 c↭d 为两条直径。
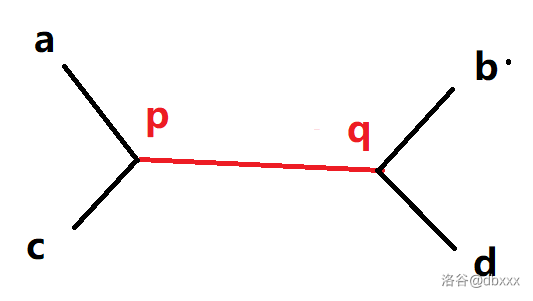
对于上面这样两条直径,有 (a∼p)=(c∼p) 且 (b∼q)=(d∼q)。下面开始证明。
根据直径长度相同,(a∼b)=(c∼d),所以 (a∼p)+(p∼q)+(q∼b)=(c∼p)+(p∼q)+(q∼d)。我们称之为直径等长式。
根据直径等长式,(a∼p)=(c∼p)⟺(b∼q)=(d∼q)。因此下面只需证明 (a∼p)=(c∼p)。
不妨设 (a∼p)>(c∼p)(如果小于就交换 a 和 c,再同时交换 b 和 d,这样 a↭b 和 c↭d 仍是两条直径)。
又根据直径等长式,可以得到 (q∼b)<(q∼d)。
所以有 (a∼p)+(p∼q)+(q∼d)>(a∼p)+(p∼q)+(q∼b),也即 (a∼d)>(a∼b)。
那么 a↭b 一定不是直径,矛盾。
上面是以 X 型为例的。Y 型可以看成是钦定 (a∼p)=(c∼p)=0 的 X 型,上述证明同样成立。
所以对 X 型的证明已经包含了对 Y 型的证明,后面相关证明将会省略 Y 型。
性质八
定义一条直径的几何中心为直径上唯一的一个点(这个点不一定是原树上的点,而可以落在这条直径的一条边上,将这条边分成任意大小比例的两段),满足它到直径两个端点的距离相同。则,一棵树上所有直径的几何中心都重合在一个点。
注:为了方便后面的叙述,我们将原树上的点正常称作”点“,将可以落在树边上任意比例将边切成两端的点称作”几何点“。
设树上存在两条直径 a↭b 和 c↭d,几何中心分别为 i 和 j。
假设 i 不在 a↭b 和 c↭d 的重合段 p↭q 上。
不妨设 i 在 a↭p 上。如果 i 在 b↭q 上,考虑同时交换 a 和 b,c 和 d,p 和 q。
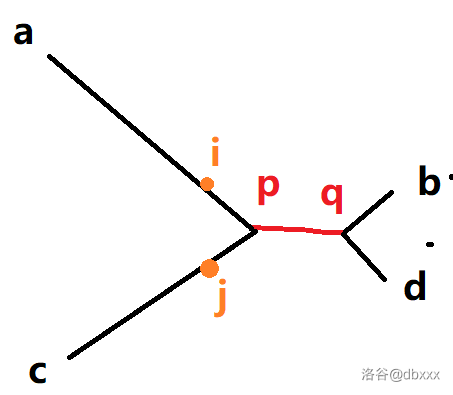
(a∼b)=(c∼d),根据中点的性质又有 (a∼i)=(i∼b)=(c∼j)=(j∼d)=21(a∼b)=21(c∼d)。
所以 (a∼b)=(a∼i)+(i∼j)+(j∼b)=(a∼b)+(i∼j)>(a∼b)。所以 a↭b 不是直径,矛盾。
因此 i 一定在这个 p↭q 的重合段上,绘图如下:
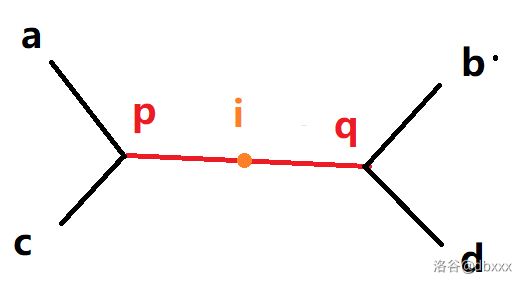
很明显 (a∼b)=(c∼d),所以 (a∼i)=(c∼j)。
而刚刚已经证明过 (a∼p)=(c∼p),所以 (a∼i)−(a∼p)=(c∼j)−(c∼p),即 (p∼i)=(p∼j)。
因为 i 没有超出重合段,所以 j 也没有超出,同时和 p 的距离也相等,因此 i 和 j 重合,结论得证。
如此以来,我们不妨设所有直径共同的那个几何中心称作 树的几何中心。接下来,我们探求树的几何中心的性质。
性质九
对于任一直径上的几何点,其到这条直径两条端点距离的最大值等于其到树中任意点距离的最大值。
当这个“几何点”就在原图上的某个点时,与性质一等价。
否则,设几何点是 p,就直接把 p 当做一个新点按在原树上。
如果原先 p 在点 u 和点 v 之间,则将 p 当做一个点,只和 u 与 v 有连边。
p 与 u 连边的权值等于 p 原先将 (u,v) 这条边的边权分成的两部分中,(p,u) 这部分的权值。
p 与 v 连边的权值为另一侧 (p,v) 这部分的权值。
很明显这不会影响到原树上的直径(硬说影响,只会让直径多一个点)。按照性质一的思路证明即可。
性质十
在树上与所有点的最大距离最小的几何点唯一,恰为树的几何中心,其与所有点的距离最大值为树的直径的一半(称作半径)。
根据性质九,树的几何中心 c 到所有点的距离最大值等于其到直径两条端点距离的最大值,恰好是半径。
设一个不为几何中心 c 的几何点 p。
如果几何点 p 在直径上,因为 p=c,其到某个端点的距离一定大于半径,那么其到所有点距离最大值也一定严格大于半径,严格比 c 劣。
如果几何点 p 不在直径上。
考虑将 c 删除,具体地:
- 如果 c 是原树上的一个点,直接将树上的这个点以及关联边删除。
- 如果 c 在原树的一个边上(且不在点上),将树上的这条边删除。
那么,因为所有直径都经过 c,任意一条直径的两条端点将不再联通。
任取一条直径,设端点为 s 和 t。由于 s 和 t 不再联通,所以 p 至少和 s 和 t 中的某个点不再联通,不妨设为 s。
因为删除几何点 c 后 p 和 s 不再联通,所以 p↭s 这条路径一定经过 c,即可以表示为 p↭c↭s。
很明显 (p∼c)>0,所以 (p∼s)>(c∼s),p 到 s 的距离大于半径,到所有点距离最大值也势必大于半径,严格比 c 劣。
证毕。
因此,
- 任意一条直径的几何中心。
- 树上到所有点最大距离最小的几何点。
上面这两种说法是等价的,描述的几何点都是唯一的一个几何点,它的名字叫树的几何中心。
性质十一
定义树的中心为,距离所有点最大距离最小的点。则,
- 如果一棵树的几何中心恰好为原树上的一个点,则该树的中心唯一,为这个点。
- 如果一棵树的几何中心落在边上(不和点重合),并且将这条边分为权值相等的两部分,则该树的中心有两个,分别为这条边的两个端点。
- 如果一棵树的几何中心落在边上(不和点重合),将这条边分成权值一大一小两部分,则该树的中心唯一,为这条边两个端点中,距离几何中心更近的那个端点。
第一种情况可以根据前几个性质平凡推得。
现在考虑一棵树的几何中心不为原树上点的情形。任取一条直径,设 s↭u⟷v↭t,并设 p 在 u⟷v 上。
根据直径几何中心 p 在 u 和 v 之间,不难得到 (u∼s)<(u∼t),(v∼s)>(v∼t)。
也即 u 离 t 更远,v 离 s 更远。根据性质一(或者更强的性质九),u 到所有点最远距离为 (u∼t),v 到所有点最远距离 (v∼s)。
考虑断开 u⟷v 后,任意一个点 x 至少不和 s 和 t 中某个点连通。
所以任意一个点 x 要么和 s 的路径经过 (u,v),要么和 t 的路径经过 (u,v)。
如果 x 和 t 的路径经过 (u,v),则 x 到 t 的路径可以表示成 x↭u⟷v↭t。
不难看出如果 x=u,则 (x∼t)=(x∼u)+(u∼t)>(u∼t),所以 x 严格比 u 劣,不是几何中心。
如果 x 和 s 的路径经过 (u,v),则 x 到 s 的路径可以表示成 x↭v⟷u↭s。
不难看出如果 x=v,则 (x∼s)=(x∼v)+(v∼s)>(v∼s),所以 x 严格比 v 劣,不是几何中心。
综上,几何中心只有可能是 u 和 v 两个点中的某一个或两个都是。
考虑第三种情况,p 没有均分 (u,v)。如果 p 与 u 的距离小于 p 与 v 的距离,即 (p∼u)<(p∼v)。
因为 (p∼s)=(p∼t)⟺(p∼u)+(u∼s)=(p∼v)+(v∼t),所以 (u∼s)>(v∼t)。
同时加上 (u∼v) 得到 (v∼s)>(u∼t)。
因此,u 严格比 v 优秀,u 是整棵树的几何中心。
否则,如果 p 与 u 的距离大于 p 与 v 的距离,则上面所有不等号倒置,得到 v 严格比 u 优秀,v 是整棵树的几何中心。
考虑第二种情况,如果 p 与 u 的距离等于 p 与 v 的距离。
这个时候上面所有不等号变成等号,会得到 u 和 v 距离所有点的最大距离都取到最小值 (v∼s)=(u∼t),此时 u 和 v 都是几何中心。
本文耗时八个小时,如果帮助到您就点个赞吧。










【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 单线程的Redis速度为什么快?
· 展开说说关于C#中ORM框架的用法!
· Pantheons:用 TypeScript 打造主流大模型对话的一站式集成库
· SQL Server 2025 AI相关能力初探
· 为什么 退出登录 或 修改密码 无法使 token 失效
2022-04-23 葵神做题反思
2022-04-23 [luogu p3507] [POI2010]GRA-The Minima Game
2022-04-23 [luogu p3214] [HNOI2011] 卡农
2022-04-23 [luogu p8255] [NOI Online 2022 入门组] 数学游戏