CF1746E Joking
CF1746E Joking
\(\{1, 2\}\)
交互库最开始给定一个正整数 \(n\)，并生成一个 \(x \in [1, n]\)，你的目标是得到交互库中的 \(x\)。
你可以向交互库提出问题：
提问一个集合 \(S\)，交互库回答的内容是 \(x \in S\) 的真假。该提问次数不能超过限制数 \(Q\)。
交互库可以骗人，也即交互库的回答不一定正确。但保证 交互库连续的两次回答中，至少有一次是正确的。
你还可以向交互库提交答案，直接提交一个正整数 \(i\)。你只有 \(2\) 次提交答案的机会。
保证 \(1 \le n \le 10^5\)。交互库是自适应性的，它会通过某种神奇策略动态改变 \(x\)，使得它仍然满足它所回答过你的所有问题，保证交互正确性的同时，尽可能让你慢地猜出答案。
E1 Easy Version
在 Easy Version 中，限制参数 \(Q = 82\)。
观察到提交答案的机会只有 \(2\) 次，因此中途就提交答案并不是特别明智。但直接放弃一次多余的机会也不是很明智。
因此我的想法是：当知道 \(x\) 的范围只有两个数的时候，直接把这两个数猜一遍就可以了。那么我们提问的最终目标从将 \(x\) 锁定成一个数弱化成了锁定成两个数的一个小范围。
对交互的询问进行分析，我们考虑交互库不骗人的时候怎么做。
我们大概能知道这种交互问题都是不断缩小 \(x\) 可能的范围得到答案的，不妨放称当前 \(x\) 可能的范围为“目标范围”，最开始目标范围就是 \([1, n]\) 的正整数全集，而我们的目标就是把目标范围减少到大小为 \(2\)。为了确保询问次数低于限制参数，我们期望每次能让目标范围降低的尽可能多。
这里让目标范围降低多少的计算，应该按照交互库的 Yes，No 两种回答中，能让目标范围降低地最少的那个来计算，也即我们要按照最坏情况考虑。
比如当前的目标范围是 \(U\)，你提问一次 \(S = \{1\}\)（我们先暂且假定交互库不骗人），那么交互库回答 Yes，不管 \(U\) 多大都能降低成 \(1\)，也即 \(U\) 的大小会降低 \(|U| - 1\)。这个降低效果没人敢说不高。但是如果交互库回答 No，目标范围大小只能降低 \(1\)，这就很不优秀了。根据按照最坏情况考虑的原则，这种询问策略的目标范围降低效果为降低 \(1\)，明显不是我们想要的策略。
提一嘴，这里交互库自适应，所以要按照最坏情况考虑；但如果交互库不自适应，那么可能可以有正确率不是 \(100\%\) 但是可以很高的交互策略：可以算一下交互库回答两种答案的期望，从而得到目标范围降低的期望，而不是最坏情况。
如果一个交互策略的最坏情况很不优秀，但是期望比较优秀，在交互库不自适应的情况下可能也是可以做的。这是后话了。
如果交互库不骗人，策略还是比较容易想到的，折半查找即可。
设当前目标范围是 \(U\)，我们取 \(U\) 的一个大小为 \(\left\lfloor\dfrac{|U|}2\right\rfloor\) 的子集 \(S\) 进行提问。如果回答 Yes，那么目标范围 \(U \gets S\)，大小变成 \(\left\lfloor\dfrac{|U|}2\right\rfloor\)，也即降低 \(\left\lceil\dfrac{|U|}2\right\rceil\)；如果回答 No，目标范围 \(U \gets \complement_US\)，大小变成 \(\left\lceil\dfrac{|U|}2\right\rceil\)，也即降低 \(\left\lfloor\dfrac{|U|}2\right\rfloor\)。
那么这种策略，每次可以将目标范围 \(U\) 大小降低 \(\left\lfloor\dfrac{|U|}2\right\rfloor\)，我们可以在 \(\log_2n\) 的询问次数解决问题。
如果交互库骗人呢？
首先我们要分析清楚的是，会骗人的交互库对于我们询问的回答，能给我们提供什么确定的信息。容易看出，在交互库骗人时，单独一次询问的回答什么信息都不能提供，如果我们只看不相邻的两次询问，也什么信息都不能提供。关键就是在于我们要利用好相邻两次询问最少有一次是真的，来看 相邻的两次询问能带来什么信息。
不过，在分析这个之前，我先介绍一个关键的思想：对于一次 \(S\) 的询问：
- 交互器回答
Yes：说明本轮交互器告诉我们 \(x\) 在 \(S\) 中。 - 交互器回答
No：说明本轮交互器告诉我们 \(x\) 在 \(\complement_US\) 中。
请注意这里对回答 No 的思考方式，我们不要直接思考 \(x\) 不在 \(S\) 中，这样会越思考越乱。正确想法应该是：对于一次 \(\boldsymbol S\) 的询问，无论交互器的回答是什么，它提供我们的信息都是 \(\boldsymbol x\) 在某个集合 \(\boldsymbol{S'}\) 里，只是回答 Yes 代表 \(S' = S\)，回答 No 代表 \(S' = \complement_US\)。这个想法的改变对于解题非常有帮助，后面大家会深刻感受到这点。
现在来看相邻的两次询问能带来什么信息。假设我们先询问一次，得到了 \(x \in S'\)（注意，根据上面的思想转变，这里 \(x \in S'\) 已经同时蕴含了交互器的两种回答），再询问一次，得到了 \(x \in T'\)，我们能得到什么信息？
这两次询问的结果在交互库不骗人时，保证均是真的，我们可以得到 \(x \in S’\) 且 \(x \in T'\) 为真，即 \(x \in S’ \cap T'\)。
而在交互库骗人时，这两条信息的真假并不确定，只保证至少有一个是真的，即：\(x \in S'\) 或 \(x \in T'\) 为真。这样我们得到的信息是 \(x \in S' \cup T'\)。请记住这个结论： 本题中相邻的两次反馈为 \(\boldsymbol{x \in {S'}}\) 和 \(\boldsymbol{x \in {T'}}\) 的询问，得到的确定性信息为 \(\boldsymbol{x \in {S' \cup T'}}\)。这个结论尤为重要，是本题根据询问回答推出确定信息的基本方法。
总结一下：通过两次相邻的，反馈分别为 \(x \in S'\) 和 \(x \in T'\) 的两次询问，可确定 \(x \in S' \cup T'\)，将目标范围 \(U\) 缩小到 \(S’ \cup T'\)，换句话说，\(\complement_U(S' \cup T') = \complement_US' \cap \complement_UT'\) 可以从全集中被删除了。
回想我们的目标，我们期望用这两次相邻的询问，让目标范围降低地尽可能多。
先梳理思路：\(S'\) 和 \(T'\) 是由你的询问和交互器共同决定的，如果你决定做两次 \(S\) 和 \(T\) 的询问，交互器对这两种询问可能有四种不同的回答，而你显然无法事先预知交互器的回答，并且交互库自适应，所以 \(S' = S\) 或 \(S' = \complement_US\)，\(T' = T\) 或 \(T' = \complement_UT\) 组成的共四种可能中，你需要按照最坏情况作为“先问 \(S\)，再问 \(T\)”的目标范围缩小效果。然后，再探求什么样的 \(S\) 和 \(T\) 能使得这个目标范围缩小效果达到最高。
还是假设当前目标范围为 \(U\)，连续两次分别询问了 \(S\) 和 \(T\)，那么：
- 两次均回答
Yes，可以将目标范围进一步锁定到 \(S \cup T\)，也即 \(\complement_U\left(S \cup T\right) = \complement_U S \cap \complement_U T\) 可以被删去。 - 第一次回答
No，第二次回答Yes，可以将目标范围进一步锁定到 \(\complement_U S \cup T\)，也即 \(\complement_U\left(\complement_U S \cup T\right) = S \cap \complement_UT\) 可以被删去。 - 第一次回答
Yes，第二次回答No，可以将目标范围进一步锁定到 \(S \cup \complement_UT\)，也即 \(\complement_U\left(S \cup \complement_UT\right) = \complement_US \cap T\) 可以被删去。 - 两次均回答
No，可以将目标范围进一步锁定到 \(\complement_US \cup \complement_UT\)，也即 \(\complement_U\left(\complement_US \cup \complement_UT\right) = S \cap T\) 可以被删去。
上面的等号用的是德摩根定律化简，读者处理集合问题应当熟练应用。
这里我们应该按照最坏情况讨论，即如果我们钦定询问第一次询问 \(S\)，第二次询问 \(T\)：
- 最坏情况下，目标范围的大小至少会缩小到 \(\max\left(\left|S \cup T\right|, \left|\complement_U S \cup T\right|, \left|S \cup \complement_UT\right|, \left|\complement_US \cup \complement_UT\right|\right)\)。
- 最坏情况下，目标范围的大小至少会减少 \(\min\left(\left|S \cap T\right|, \left|\complement_U S \cap T\right|, \left|S \cap \complement_UT\right|, \left|\complement_US \cap \complement_UT\right|\right)\)。
当然，上面两条是等价的，这里我选择第二条处理（选第一条处理也很好做，读者可以自行尝试）。
我们的目标是最大化缩小效果，也即选定 \(S\) 和 \(T\)，最大化 \(\min\left(\left|S \cap T\right|, \left|\complement_U S \cap T\right|, \left|S \cap \complement_UT\right|, \left|\complement_US \cap \complement_UT\right|\right)\)。
对于集合问题我们可以考虑绘制韦恩图。
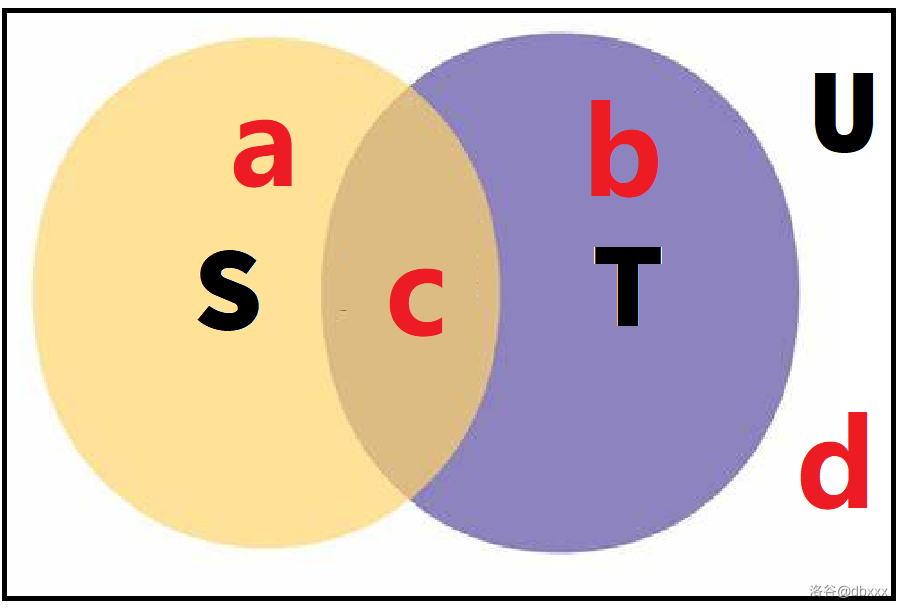
设上面黄色区域代表的集合为 \(S_1\)，大小为 \(a\)；紫色区域代表的集合为 \(S_2\)，大小为 \(b\)；棕色区域代表的集合为 \(S_3\)，大小为 \(c\)；白色区域代表的集合为 \(S_4\)，大小为 \(d\)。
容易发现，\(S_1\)，\(S_2\)，\(S_3\)，\(S_4\) 互不相交，并集为 \(U\)，即 \(a +b +c + d = |U|\)。
观察目标最值的四项：\(\min\left(\left|S \cap T\right|, \left|\complement_U S \cap T\right|, \left|S \cap \complement_UT\right|, \left|\complement_US \cap \complement_UT\right|\right)\)。
我们可以发现，\(S_1 = S \cap \complement_UT\)，\(S_2 = \complement_US \cap T\)，\(S_3 = S \cap T\)，\(S_4 = \complement_US \cap \complement_UT\)，也即目标最值中的四项恰好和韦恩图中的四个小区域是完全对应的。
那么目标最值其实就是 \(\min(a, b, c, d)\)，我们期望它最大。
\(a\)，\(b\)，\(c\)，\(d\) 作为和为 \(|U|\) 的正整数，它们的最小值最大就是 \(\left\lfloor\dfrac{|U|}4\right\rfloor\)。构造也比较简单，先令 \(a = b = c = d = \left\lfloor\dfrac{|U|}4\right\rfloor\)，此时 \(a +b +c +d\) 距离 \(|U|\) 还剩 \(|U| \bmod 4\)，将 \(|U| \bmod 4\) 随意地加在这四个数中即可。
目标最值已求出，那么我们将 \(U\) 尽可能平均分为四个子集 \(S_1\)，\(S_2\)，\(S_3\)，\(S_4\)（最小的子集大小为 \(\left\lfloor\dfrac{|U|}4\right\rfloor\) 即视作完成平均分），然后令 \(S = S_1 \cup S_3\)，\(T = S_2 \cup S_3\)，这样就构造出了一组可以让目标集合 \(U\) 最坏情况下也至少减少 \(\left\lfloor\dfrac{|U|}4\right\rfloor\) 的询问策略。
回顾我们的构造方案，事实上，我们是将 \(U\) 分成了四个集合，然后选取了一种询问策略，使得无论回答如何，我们总能将四个集合之一扔出目标集合。并且这四个集合中最小的那个也至少有四分之一，使得最坏情况下我们总能将目标集合减少四分之一。
现在我们检验这样的询问策略能否达成目标。写程序判断需要用多少询问才能把目标集合大小缩小到 \(2\) 以内（别忘了我们有两次猜测机会）：
int main() {
int n = (int)1e5;
for (int i = 0; i <= 83; i += 2, n - (n >> 2))
std :: cout << i << ' ' << n << std :: endl;
return 0;
}
我们发现用 \(76\) 次询问即可让目标集合的大小降至 \(3\)，似乎下降的速度还可以，但后面无论使用多少次询问目标集合大小仍然是 \(3\)，想一下为什么。
其实很简单，我们每次能让目标集合减少 \(\left\lfloor\dfrac{|U|}4\right\rfloor\)，然而 \(|U| = 3\) 的时候这个值是 \(0\)，也就是压根无法减少。
分析原因，其实是因为 \(|U| = 3\) 的时候，不妨设 \(U = \{p, q, r\}\)，我们将其划分成四个子集，发现其中必须有一个是空的。这意味着我们的询问可能有一种回答，对目标集合的变化是：从 \(U\) 里扔掉了一个空集。这是无法化简问题的。
更具体来说，假设我们的划分是 \(S_1 = \{p\}\)，\(S_2 = \{q\}\)，\(S_3 = \{r\}\)，\(S_4 = \varnothing\)，问题为 \(S = S_1 \cup S_3\)，\(T = S_2 \cup S_3\)。那么在 \(S\) 和 \(T\) 均回答 Yes 时，我们的推论是目标集合变小到 \(S \cup T\)，也即扔掉了 \(S_4\)，这相当于什么也没扔。
或者假设划分是 \(S_1 = \{p\}\)，\(S_2 = \{q\}\)，\(S_3 = \varnothing\)，\(S_4 = \{r\}\)，问题为 \(S = S_1 \cup S_3\)，\(T = S_2 \cup S_3\)。那么在 \(S\) 和 \(T\) 均回答 No 时，我们的推论是目标集合变小到 \(\complement_US \cap \complement_UT\)，也即扔掉了 \(S_3\)，也造成了扔空集。
那么我们只能换一种策略了。既然 \(76\) 次询问就能让目标集合大小减少到 \(3\)，我们还有 \(6\) 次询问机会让它的大小减少到 \(2\)。
这里你可以尝试手玩一下（笔者其实手玩花了不少时间）。这里提供一种 \(3\) 次询问解决问题的策略：
先问一次 \(\{p\}\)，如果是 No，再问一次 \(\{p\}\)，如果还是 No，那么目标集合可缩减到 \(\{q, r\}\)。
否则，上一个状态应该是问了一次 \(\{p\}\) 得到了一个 Yes。然后直接问 \(\{q\}\) 即可。回答 Yes 目标集合为 \(\{p, q\}\)，否则为 \(\{p, r\}\)。
其实这个策略是可以推广的，上面的 \(p\)，\(q\)，\(r\) 换成集合，我们就得到了一种使用 \(3\) 个问题让目标集合大小减少 \(\left\lfloor\dfrac{|U|}3\right\rfloor\) 的做法。事实上这个减少速率是比使用 \(2\) 个问题让目标集合大小减少 \(\left\lfloor\dfrac{|U|}4\right\rfloor\) 要慢的，最坏需要 \(84\) 次询问才能让目标集合降低到 \(2\) 以内，不过这题好像没卡这个做法。
于是，我们使用了不多于 \(79\) 次询问解决了本题。
#include <bits/stdc++.h>
inline int read() {} // 读入数字的函数，省略
inline std :: string rest() {} // 读入字符串的函数，省略
inline bool query(std :: vector <int> v) {
printf("? %d ", (int)v.size());
for (int x : v)
printf("%d ", x);
puts("");
fflush(stdout);
return (rest() == " YES");
}
inline void solve(std :: vector <int> v) {
int n = (int)v.size();
if (n <= 2) {
for (int x : v) {
printf("! %d\n", x);
fflush(stdout);
if (rest() == " :)")
exit(0);
}
} else if (n == 3) {
if (!query({v[0]}) && !query({v[0]})) {
solve({v[1], v[2]});
} else if (query({v[1]})) {
solve({v[0], v[1]});
} else
solve({v[0], v[2]});
} else {
std :: vector <int> S;
std :: vector <int> T;
for (int i = 0; i < n; ++i) {
if (i & 1)
S.push_back(v[i]);
if (i & 2)
T.push_back(v[i]);
}
std :: vector <int> nxt;
int s = query(S) ? 1 : 0, t = query(T) ? 2 : 0;
for (int i = 0; i < n; ++i)
if (((i & 1) == s) || ((i & 2) == t))
nxt.push_back(v[i]);
solve(nxt);
}
}
int main() {
int n = read();
std :: vector <int> v;
for (int i = 1; i <= n; ++i)
v.push_back(i);
solve(v);
return 0;
}
E2 Hard Version
在 Hard Version 中，限制参数 \(Q = 53\)。
观察我们刚才的询问策略哪里可以优化。我们从全局上查看刚才的询问策略，发现第一次询问和第二次询问是一组；第三次询问和第四次询问是一组；第五次询问和第六次询问是一组。每一组询问，我们将目标范围缩小。
然而这样“相邻两个询问必有一真”这个条件只在一组询问中的两个询问被用到；而上一组的最后一个询问和下一组的第一个询问也是相邻的，这两个询问之间也是有条件的，但我们没用到，造成了条件的浪费。
现在我们考虑怎么让每两个相邻询问的限制都用上。
一般地，假设当前的目标范围为 \(U\)，上一次询问交互库告诉我们 \(x\) 在 \(T\) 中，我们探求这次该怎么问。
很明显，我们问的集合一定是 \(U\) 的子集，并且一部分（可空）在 \(T\) 中，一部分（可空）在 \(\complement_UT\) 中。这里设 \(F = \complement_UT\)，并且询问集合在 \(T\) 中的部分为 \(T_0\)，在 \(F\) 中的部分为 \(F_0\)，即这次问的集合为 \(T_0 \cup F_0\)。并设 \(T_1 = T \setminus T_0\)，\(F_1 = F \setminus F_0\)。
如果这次的回答是 Yes，即这次询问交互库告诉我们 \(x\) 在 \(T_0 \cup F_0\) 中，我们可以确认 \(x\) 在 \(T \cup (T_0 \cup F_0) = T \cup F_0\) 中，因此目标集合 \(U \gets T \cup F_0\)，\(F_1\) 被丢出目标集合。同时，\(T \gets T_0 \cup F_0\)，以便下一次询问知道上一次询问交互库告知的信息。
如果这次的回答是 No，即这次询问交互库告诉我们 \(x\) 在 \(T_1 \cup F_1\) 中，可以确认 \(x\) 在 \(T \cup (T_1 \cup F_1) = T \cup F_1\) 中，\(U \gets T \cup F_1\)，\(F_0\) 被丢出目标集合，同时 \(T \gets T_1 \cup F_1\)。
这是一个类似 dp 的转移，考虑设计状态 \(f(U, T)\) 表示当前全集为 \(U\)，上一次询问交互库告诉我们 \(x \in T\) 时，最少的询问次数。这样并无问题，然而 \(F = U \setminus T\) 和其子集的信息在转移中大量用到，\(U\) 反而不怎么用到，如果每次表示 \(F\) 和其子集都要用 \(U \setminus T\) 来做中间桥梁，不是很直观。
因为 \(F\)，\(U\)，\(T\) 显然知二求一，不妨设 \(f(T, F)\) 表示上一次询问交互库告诉我们 \(x \in T\) 中，且 \(F = U \setminus T\) 时，最少的询问次数。
这样以来我们还要得知 \(F\) 转移时的变化，简单推理一下：
- 回答是
Yes，则 \(U \gets T \cup F_0\)，\(T \gets T_0 \cup F_0\)，\(F\) 仍应该是新的 \(U\) 和 \(T\) 的差集，并且 \(T \cup F_0\)，\(T_0 \cup F_0\) 中的并集都是两个不交集合的并，所以 \(F \gets T \setminus T_0\)，即 \(F \gets T_1\)。 - 回答是
No，则 \(U \gets T \cup F_1\)，\(T \gets T_1 \cup F_1\)，所以 \(F \gets T \setminus T_1\)。即 \(F \gets T_0\)。
于是我们可以写出转移方程：
这里 \(\min\) 的含义是：在当前 \((T, F)\) 这个状态下，我们可以且仅可以在 \(T\) 中选出子集 \(T_0\)，以及在 \(F\) 中选出子集 \(F_0\) 来询问。在不同的询问方式中，我们期望一个能让接下来的步数最小的询问方式来询问。
这里 \(\max\) 的含义是：在我们决定问 \(T_0 \cup F_0\) 后，交互库会返回 Yes 和 No 两种情况。交互库返回什么是我们不可预测的，并且因为交互库的自适应性，我们必须按照最坏的一种情况考虑。也即，对于 \(T_0 \cup F_0\) 的询问集合，它的后继询问步数应该取本次询问回答 Yes 和本次询问回答 No 后，两个后继询问步数的最大值。
边界状态是：\(|T \cup F| \le 2\) 时，\(f(T, F) = 0\)。
询问的方式是：在当前 \((T, F)\) 的状态下，考虑能让这个 \(\min\) 取到最小值的一对 \((T_0, F_0)\)，然后询问 \(T_0 \cup F_0\) 即可。
可以认为在第一次询问之前，交互器告诉了我们 \(x \in \{1, 2, \ldots, n\}\) 整个全集，因此初始状态是 \((\{1, 2, \ldots, n\}, \varnothing)\)。
然而这样的状态本身的复杂度就能达到 \(4^n\) 量级，显然无法承受。观察到，我们的询问策略显然和 \(T\) 和 \(F\) 这两个集合的具体形态没什么关系，只和它们的大小有关。也即，对于 \(|T_1| = |T_2|\)，\(|F_1| = |F_2|\)，我们有 \(f(T_1, F_1) = f(T_2, F_2)\)。
因此，我们考虑不将集合设入状态，而是将集合的大小设入状态。于是我们可以得到如下转移方程：
边界状态是：\(a + b \le 2\) 时，\(f(a, b) = 0\)。
询问的方式是，在当前 \((T, F)\) 的状态下，考虑 \(a = |T|\)，\(b = |F|\)，以及能让 \(f(a, b)\) 这个 \(\min\) 取到最小值的一对 \((c, d)\)，然后在 \(T\) 中随便选一个大小为 \(c\) 的子集 \(T_0\)，\(F\) 中随便选一个大小为 \(d\) 的子集 \(F_0\)，询问 \(T_0 \cup F_0\) 即可。
初始状态是 \(f(n, 0)\)。
观察转移的顺序并检查转移的无环性：对于任意 \(f(a, b)\)，为了转移计算它的值用到的 \(f(a', b')\) 一定满足 \(c + d \le a + b\)，因为每次询问后目标全集一定没有变大。为验证，计算一下 \(f(c+ d, a - c)\) 中两个维上值的和 \(a + d\)，以及 \(f(a +b - c - d, c)\) 中两个维上值的和 \(a + b - d\)，它们确实不会超过 \(a + b\)。所以，我们的转移大体顺序一定是先转移并计算 \(a + b\) 小的 \(f(a, b)\)。
那么对于 \(a + b = a' + b'\)，\(f(a, b)\) 和 \(f(a, b')\) 应该先转移谁？考虑到如果我们花费了一次提问，使得当前的全集 \(T \cup F\) 没有增加，但是 \(F\) 反而变少了，这样是一定不优的。因为每次我们都是在 \(F\) 中选择一个子集抛出全集，因此我们当然希望 \(F\) 尽可能大，从而使得能选择抛出全集的 \(F\) 的子集尽量大。因此对于 \(a + b = a' + b'\)，不妨令 \(b > b'\)，我们应该令 \(f(a, b)\) 去转移 \(f(a',b')\)（\(f(a', b')\) 要比 \(f(a, b)\) 后转移到）。
事实上，\(f(a, b)\) 若用到 \(a' +b' = a + b\) 的 \(f(a', b')\) 转移，意味着 \(d = 0\) 或 \(d = b\)，也就是我们选择的 \(F_0 = \varnothing\) 或 \(F_0 = F\)（即 \(F_1 = \varnothing\)），这均会导致计算分别扔掉 \(F_0\)，\(F_1\) 时至少有一种丢了空集，也即目标集合大小不变。
至于 \(f(a, b)\) 转移用到自己的情况，意味着最坏情况下这次询问可能会让 \((F, T)\) 毫无变化，显然这样的询问是浪费的，不可取，直接不转移即可（其实不用特殊处理，因为 \(f(a, b) + 1\) 一定无法作为更小的值更新 \(f(a, b)\)）。
以 \(a + b\) 升序为第一优先级，\(b\) 降序为第二优先级，这样转移是一定无环的，转移顺序就解决了。
考虑到上面的状态复杂度为 \(n^2\)，转移时间复杂度为 \(\Theta(n^4)\)，显然无法承受。怎么办？
这里有一种启发式的思想，不妨从 E1 尽可能让全集大小降速更快的角度思考转移的过程。
当前的状态是 \((T, F)\)，每次我们选定 \(T_0 \cup F_0\)，根据上面的讨论，交互库回答 Yes 时，状态变为 \((T_0 \cup F_0,T_1)\)，\(F_0\) 被丢出集合；否则变为 \((T_1 \cup F_1, T_0)\)，\(F_1\) 被丢出集合。我们希望最坏情况下被丢的尽可能多，所以令 \(\min(|F_0|, |F_1|)\) 取最大，让 \(F_0\) 均分 \(F\) 比较合适。而且我们还希望最坏情况下，下次的 \(F\) 也能尽量大（这样下一次丢的 \(F_0\) 或 \(F_1\) 也能尽量大）所以令 \(\min(|T_0|, |T_1|)\) 最大，还是让 \(T_0\) 均分 \(T\) 比较合适。
因此，我们考虑让转移方程中的 \(c\) 和 \(d\) 只在 \(\dfrac a 2\) 和 \(\dfrac b 2\) 附近几个整数枚举，这样以来枚举复杂度就会降低成 \(\Theta(n^2)\)。这样以来 \(f(a, b)\) 的内容可能不再是最少步数，但经试验，它的内容也是一个相对较少的步数（只不过不是最优解而已）。本题中，我们并不关心最优步数的具体精确值，只需要得到一个足够少步数的方案，所以这样是可行的。
这里我取 \(c \in \left[\left\lfloor\dfrac{a - 1}2\right\rfloor, \left\lceil\dfrac{a}{2} \right\rceil + 1\right]\)，\(d \in \left[\left\lfloor\dfrac{b - 1}2\right\rfloor, \left\lceil\dfrac b 2 \right\rceil + 1\right]\)。
然而 \(n^2\) 还是过不了 \(10^5\)。我们不妨再次启发式一下，真的需要用到所有状态吗？如果我们只想知道 \(f(n, 0)\) 的值，实际需要的状态数是不是会少于 \(n^2\)，乃至于可以接受呢？我们可以用记忆化搜索进行尝试。
typedef std :: pair <int, int> pii;
std :: map <pii, int> f;
std :: map <pii, pii> g;
inline int F(int a, int b) {
if (a + b <= 2)
return 0;
if (f.count({a, b}))
return f[{a, b}];
int ans = 1000, ansc = -1, ansd = -1;
for (int c = std :: max(0, (a - 1) >> 1); c <= std :: min(a, (a + 3) >> 1); ++c)
for (int d = std :: max(0, (b - 1) >> 1); d <= std :: min(b, (b + 3) >> 1); ++d) {
if ((c + d) + (a - c) == a + b && a - c <= b)
continue;
if ((a + b - c - d) + c == a + b && c <= b)
continue;
// 上面两行是为了控制 a + b = a' + b' 时的转移顺序
// 注意 a - c <= b, c <= b 的等号不能省略，这是为了防止 F(a, b) 的求解访问自身导致死递归
int now = 1 + std :: max(F(c + d, a - c), F(a + b - c - d, c));
if (now < ans) {
ans = now;
ansc = c;
ansd = d;
}
}
g[{a, b}] = {ansc, ansd};
return f[{a, b}] = ans;
}
调用 F(1e5, 0) 我们可以发现，这样运行后 \(f\) 的大小为 \(3947\)，这个状态数无疑是十分优秀的。
注意到初始时我们应该调用 \(F(n, 0)\) 而非 \(F(10^5, 0)\)，这是因为 \(F(10^5, 0)\) 访问到的所有状态可能不含有 \(F(n, 0)\) 所需的状态。另外，\(F(n, 0)\) 并不是 \(n\) 越大状态数越多，比如 \(F(10^5 - 3, 0)\) 访问到的状态数为 \(3953\)。然而，\(n\) 越大状态数确实呈现越多的趋势，不可能 \(n\) 变小时状态数突然暴涨，因此我们可以推断 \(F(n, 0)\) 的状态数大概就是 \(4000\) 的量级。
而且 \(f(10^5, 0)\) 恰好为 \(53\)，恰好满足要求，至此本题解决。
由于本题过于启发式，时间复杂度笔者写不出来。
/*
* @Author: crab-in-the-northeast
* @Date: 2023-06-20 19:58:38
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2023-06-20 21:59:36
*/
#include <bits/stdc++.h>
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
inline std :: string rest(bool space = true) {
std :: string s;
char ch = getchar();
for (; !isgraph(ch); ch = getchar());
for (; isgraph(ch); ch = getchar())
s.push_back(ch);
return space ? (" " + s) : s;
}
typedef std :: pair <int, int> pii;
std :: map <pii, int> f;
std :: map <pii, pii> g;
inline int F(int a, int b) {
if (a + b <= 2)
return 0;
if (f.count({a, b}))
return f[{a, b}];
int ans = 1000, ansc = -1, ansd = -1;
for (int c = std :: max(0, (a - 1) >> 1); c <= std :: min(a, (a + 3) >> 1); ++c)
for (int d = std :: max(0, (b - 1) >> 1); d <= std :: min(b, (b + 3) >> 1); ++d) {
if ((c + d) + (a - c) == a + b && a - c <= b)
continue;
if ((a + b - c - d) + c == a + b && c <= b)
continue;
int now = 1 + std :: max(F(c + d, a - c), F(a + b - c - d, c));
if (now < ans) {
ans = now;
ansc = c;
ansd = d;
}
}
g[{a, b}] = {ansc, ansd};
return f[{a, b}] = ans;
}
inline bool ask(std :: basic_string <int> S) {
printf("? %d ", (int)S.size());
for (int x : S)
printf("%d ", x);
puts("");
fflush(stdout);
return (rest() == " YES");
}
inline void solve(std :: basic_string <int> T, std :: basic_string <int> F) {
int a = (int)T.size(), b = (int)F.size();
if (a + b <= 2) {
std :: basic_string <int> ans = T + F;
for (int x : ans) {
printf("! %d\n", x);
fflush(stdout);
if (rest() == " :)")
exit(0);
}
} else {
auto p = g[{a, b}];
int c = p.first, d = p.second;
std :: basic_string <int> T0, T1, F0, F1;
T0.assign(T.begin(), T.begin() + c);
T1.assign(T.begin() + c, T.end());
F0.assign(F.begin(), F.begin() + d);
F1.assign(F.begin() + d, F.end());
if (ask(T0 + F0))
solve(T0 + F0, T1);
else
solve(T1 + F1, T0);
}
}
int main() {
int n = read();
F(n, 0);
std :: basic_string <int> S;
S.resize(n);
std :: iota(S.begin(), S.end(), 1);
solve(S, {});
return 0;
}
