放球问题 学习笔记

前言

今天，我们来讨论一个非常有意思的问题——放球问题（又称球盒问题）。

放球问题，顾名思义，是求解将 $n$ 个球放进 $m$ 个盒子的方案数的问题。

而这个问题有意思的地方在于：球有无区别，盒有无区别，盒可否空放， $n$ 和 $m$ 的大小都能影响到问题的最终结果。因此，我们把这个问题细分为十六个小问题：

1. 球无区别，盒无区别，盒无空放，$n \ge m$。
2. 球无区别，盒无区别，盒无空放，$n < m$。
3. 球无区别，盒无区别，盒可空放，$n \ge m$。
4. 球无区别，盒无区别，盒可空放，$n < m$。
5. 球无区别，盒有区别，盒无空放，$n \ge m$。
6. 球无区别，盒有区别，盒无空放，$n < m$。
7. 球无区别，盒有区别，盒可空放，$n \ge m$。
8. 球无区别，盒有区别，盒可空放，$n < m$。
9. 球无区别，盒无区别，盒无空放，$n \ge m$。
10. 球有区别，盒无区别，盒无空放，$n < m$。
11. 球有区别，盒无区别，盒可空放，$n \ge m$。
12. 球有区别，盒无区别，盒可空放，$n < m$。
13. 球有区别，盒有区别，盒无空放，$n \ge m$。
14. 球有区别，盒有区别，盒无空放，$n < m$。
15. 球有区别，盒有区别，盒可空放，$n \ge m$。
16. 球有区别，盒有区别，盒可空放，$n < m$。

根据这些，我们还可以给这16个问题一个代码。

我们规定：

• 球有区别为1，球无区别为0
• 盒有区别为1，盒无区别为0
• 盒可空放为1，盒无空放为0
• $n \ge m$ 为1，$n < m$ 为0

根据这个给不同问题类型赋予一个代码。比如第11号问题球有区别，盒无区别，盒可空放，$n \ge m$，可简化为1011问题。

球盒区别解释

假设$n = 3, m = 2$，对球编号 $1, 2, 3$：

为方便，规定类似于如下的表示：{1, 2}, {3} 表示第一个盒子中有1,2两个球，第二个盒子中有3一个球

而且无论十六种问题中哪一种，对于单个盒子而言，即使球有区别，盒子内部球的顺序永远只算一种情况。也就是说 {1, 2}, {3} 和 {2, 1}, {3} 只能算作一种情况（无论 16 种问题的哪一个。）

如果球有区别，盒也有区别，那么除了上一句说的情况外，其他所有的都各自算各自的情况。比如：

{1, 2}, {3}, {3}, {1, 2}, {1, 3}, {2} 这三种情况每一种都是不同的。

如果球无区别，意味着将来自两个盒子的两个球进行交换是算作一种情况的。比如：

{1, 2}, {3} 和 {1, 3}, {2} 是一种情况。

如果盒无区别，意味着将任意两个盒子调换位置是算作一种情况的。比如：

{1, 2}, {3} 和 {3}, {1, 2} 是一种情况。

那么如果球和盒都没有区别……

{1, 2}, {3}, {3}, {1, 2}, {1, 3}, {2}, {2, 3}, {1}, {2}, {1, 3} 等都是一种情况。

在球和盒都没有区别的模型下，还可以创造新的情况吗？

{}, {1, 2, 3}，可以将一个盒子清空，这样就可以创造另一种情况了。同理，{1, 2, 3}, {} 和 {}, {1, 2, 3} 是一种情况，因为盒子没有区别。

在球和盒都没有区别的模型下，必须有空的集合才能有别的情况吗？当然不是。不妨考虑扩展到 4 个球。那么：

{}, {1, 2, 3, 4}，{1}, {2, 3, 4}，{1, 2}, {3, 4} 就是三种情况。

言归正传。回到这16个问题，根据解法可以分为5种：

1. 无解
2. 排列
3. 组合
4. 母函数
5. 第二类斯特林数

接下来我们分别从这5种来开始我们的放球之旅。

无解

0000，0100，1000，1100

无解的问题是这四个问题：0000，0100，1000，1100。观察到他们的末两位都是00，回到代码定义，发现是盒不可空放，但 $n < m$。

盒比球多，不可能没有盒是空盒，所以这四个问题是无解的。（方案数为 $0$）

排列

1110，1111

也就是说，球有区别，盒有区别，允许有空盒。

这种情况下，每一个球都有 $m$ 种可能性（$m$ 个盒子中选一个放进去），所以答案是 $m ^ n$。

组合

0101

前面都比较简单，这里就开始上高速啦，跟蟹蟹系好安全带哦！

解释一下问题：球无区别，盒有区别，不允许有空盒。

那么就可以不对球进行编号了。直接把每个球看成X。

也就是将 $n$ 个 X 放进 $m$ 个盒子中。

比如 $n = 6$ 吧：

X X X X X X

放进 $m$ 个盒子，也就是把这个序列分成 $m$ 段。如果你想分段，那就必须得有分段符。比如我想把这些球分成两个盒子，其中一种情况就可以如此表示：

X X|X X X X

这就代表了前两个球放在第一个盒子中；后四个球放在第二个盒子中。

如果是分成三个盒子呢？其中一种情况就可以表示如下：

X X|X|X X X

也就是说如果分成 $m$ 个盒子，你就需要 $m - 1$ 个分段符。 分段符有点抽象，既然球盒都是具体的，那么分段符也想成一个具体的东西吧——板子！

这些板子是插在空隙中的，观察到这里有 $6$ 个球，因此空隙有 $5$ 个。一般化，$n$ 个球，空隙就会有 $n - 1$ 个。

问题就转化成了，插 $m - 1$ 个板子进 $n - 1$ 个缝隙的方案数。或者说，$n - 1$ 个空隙中选择 $m - 1$ 个空隙进行插板。

由于盒子非空，因此可以保证，每个空隙最多一个板子。因此，问题的答案就很明显了——$\dbinom{n - 1}{m - 1}$。

因此，0100问题的方案数为 $\dbinom{n - 1}{m - 1}$。

0110，0111

这两种情况和上一种情况的区别在于，盒子可以是空的了。

考虑化归，将有空盒的问题转化为无空盒的问题。

考虑构造 $n + m$ 球 $m$ 盒的 0101 问题（上面那个问题）。然后我们发现，对于每一种方案，将每个盒子都去掉 $1$ 个球，正好就对应了一种 $n$ 球 $m$ 盒的 0110/0111 方案（转化为可空）。

而且不难发现，这种对应全面且唯一，存在一一映射关系，因此 $n$ 球 $m$ 盒的 0110/0111 方案数等于 $n + m$ 球 $m$ 盒的 0101 方案数。

得到答案 $\dbinom{m + n - 1}{m - 1}$，即 $\dbinom{m + n - 1}{n}$。原因：$\dbinom{m + n - 1}{m - 1} = \dbinom{m + n - 1}{m + n - 1 - (m - 1)} = \dbinom{m + n - 1}{n}$

即，0110和0111问题的答案为：$\dbinom{m + n - 1}{n}$。

母函数

0011

球无区别，盒无区别，盒可空放。

这个方案数是没有通用公式表示的，但是可以用母函数间接表示。

如果你还没有学到有关于母函数相关内容，直接用不降序列枚举就可以了，可以跳过此部分；如果你学到了有关母函数相关内容，请接着往下看。

显然，这个问题就相当于将 $n$ 拆分成最多 $m$ 个数之和的方案数，等价于用最大数为 $m$ 的整数来分拆 $n$ 的方案数。（具体证明此处略）其母函数为：

$$G(x) = (1 + x + x ^ 2 + \cdots)(1 + x ^ 2 + x ^ 4 + \cdots)\cdots(1 + x ^ m + x ^ {2m} + \cdots) = \dfrac{1}{(1 - x)(1 - x ^ 2)\cdots(1 - x ^ m)}$$

那么，0011问题的方案数即为 $G(x)$ 的 $x ^ n$ 项系数。

0010

此时盒比球多，而既然所有球和盒都是无区别的，不妨把那 $m - n$ 个多余的盒子扔掉，然后转化为将 $n$ 拆分成最多 $n$ 个数之和的方案数即可。母函数变为如下：

$$G(x) = (1 + x + x ^ 2 + \cdots)(1 + x ^ 2 + x ^ 4 + \cdots)\cdots(1 + x ^ n + x ^ {2n} + \cdots) = \dfrac{1}{(1 - x)(1 - x ^ 2)\cdots(1 - x ^ n)}$$

其实就是把 $m$ 换成了 $n$ 而已，最后还是求 $G(x)$ 的 $x ^ n$ 项系数。

0001

此时盒不可以空放了。类比于在组合数学中我们采用的化归，这里我们也用一下化归：在每个盒子中放一个球，然后用同样的母函数：

$$G(x) = (1 + x + x ^ 2 + \cdots)(1 + x ^ 2 + x ^ 4 + \cdots)\cdots(1 + x ^ m + x ^ {2m} + \cdots) = \dfrac{1}{(1 - x)(1 - x ^ 2)\cdots(1 - x ^ m)}$$

当然了最后还得把那些球去掉，也就是说0001问题的方案数为 $G(x)$ 的 $x ^ {n - m}$ 项系数。

第二类斯特林数

1001

球有区别，盒无区别，盒无空放。

这个问题其实就是第二类斯特林数的定义，因此答案就是 $\operatorname{S}(n, m)$。

但是，这个东西怎么求呢？

有两种求法：

递推

有如下递推式：$\operatorname{S}(n, m) = \operatorname{S}(n - 1, m - 1) + m\operatorname{S}(n - 1, m)$。

其实就是讨论新来的这个球是自己独占一盒还是放到以前的盒子里边。

容斥

$$\operatorname{S}(n, m) = \dfrac{1}{m!}\sum^m_{k = 0}(-1)^k\dbinom{m}{k}(m - k) ^ n$$

枚举空盒的个数 $k$，剩下的随意放置。

因为盒子没有区别，所以最后要乘 $\dfrac{1}{m!}$ 去重。

我们又可以注意到这个式子是一个卷积，因此可以在 $\operatorname{O}(n \log n)$ 求出 $\operatorname{S}(n, k)$。这对后续说的求和也是有帮助的。

1011

盒子可以空放了，那么枚举空盒个数累计第二类斯特林数即可。答案为：

$$\sum ^ m _ {k = 1}\operatorname{S}(n, k)$$

1010

盒子比球多，扔掉多余的盒子，还是一样的套路枚举空盒个数累计第二类斯特林数。

$$\sum ^ n _ {k = 1}\operatorname{S}(n, k)$$

另提一嘴，有一个东西叫做Bell数，其定义就是这个问题。因此我们还得到了一个关于Bell数的性质：

$$\operatorname{B}(n) = \sum ^ n _ {k = 1}\operatorname{S}(n, k)$$

有关Bell数的其他结论，这里不做多介绍。但是它和斯特林数同样有趣，推荐看看哦。

1101

就是斯特林数从盒无区别变成了盒有区别。乘个盒子的全排列就OK了。

答案是 $m!\operatorname{S}(n, m)$。

总结

到现在为止，我们已经得出了这16个问题的所有答案，接下来我们列个表：

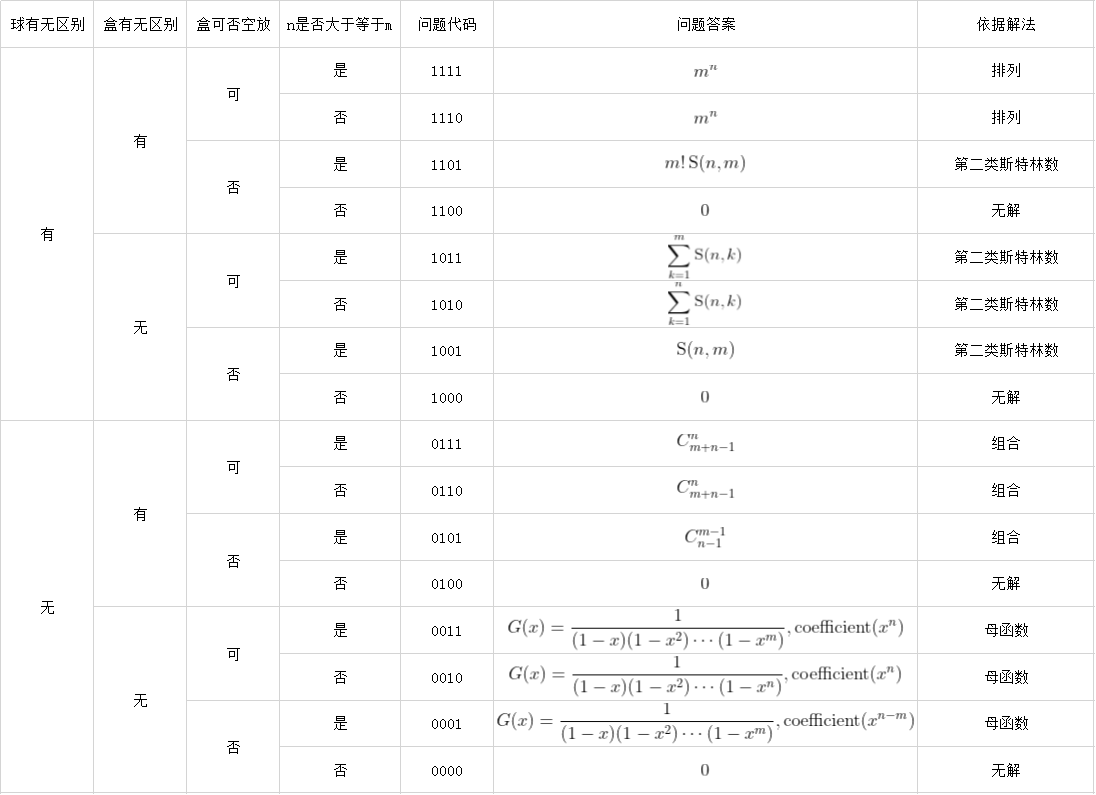
以后再遇到类似问题，对照这个表就可以啦~

另外，放球问题真的十分有意思，很能锻炼人的思维能力呢。

参考资料

• 放球问题-百度百科
• 第二类斯特林数总结 - Deadecho - 博客园