分离变量法用于求解偏微分方程和边界条件都是线性和齐次的情形。
1. 线性

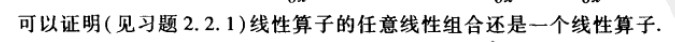
u的线性方程具有形式:
L(u)=f, 其中L是一个线性算子,f是已知的。
2. 齐次
在L(u)=f,中,如果f=0,则该方程称为齐次线性方程。检验一个方程是否为齐次方程最简单的办法就是,将恒等于0的函数带入,如果满足,则为齐次方程。
3. 线性方程解叠加原理

以上讨论同样适用于边界条件。一定要注意分离变量法的使用条件。
4. 在有限端处具有零温度的热传导方程
首先研究一维无热源问题,方程如下,这是一个方程和边界条件都是齐次线性的问题,可以使用分离变量法求解。
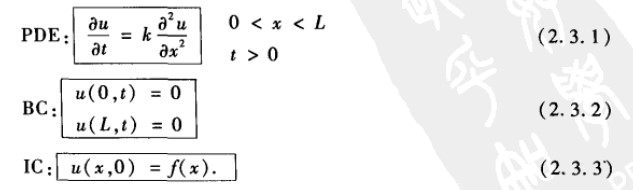
求解步骤:
(1)乘积解形式
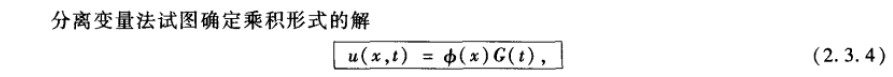
这里先不考虑初始条件。(2.3.4)必须满足2.3.1和2.3.2。
(2)分离变量
将(2.3.4)带入(2.3.1),并在两段同时除以可以分离变量:

两边要相等,只能等于一个相同的常数。

其中,λ是一个任意常数,称为分离常数。负号是为了方便才引入的,后面会解释。
这样,(2.3.7)衍生出两个常微分方程,一个是关于时间的不定常方程,一个是关于空间的。

另外,从边界条件,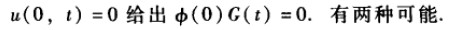
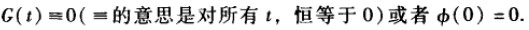
当G(t)=0, u(x,t)=0,它显然满足齐次方程,但是没多少意义,这称为平凡解。我们要寻找非平凡解。因此,边界条件变化为:


(3)不定常方程
先求解关于时间的不定常方程(2.3.9)。这是一个常系数的一阶齐次线性常微分方程。几乎所有的常系数(线性和齐次的)常微分
方程都可以通过寻找指数形式\(G=e^{rt}\)的解来求解。通过代换,特征多项式为\(r=-{\lambda}k\),因此,得到方程(2.3.9)的通解为:
\(G(t) = ce^{-\lambda kt}\)
从这个式子我们发现,由于热传导问题的解不会随时间依指数增长,因此,\(\lambda>=0\),这就显示了在分离常数中引入负号的方便之处。
(4)边值问题
乘积解中的\(\phi (x)\)满足带有两个齐次边界条件的二阶常微分方程:

没有简单的理论保证这类问题的解存在或解是唯一的。另外注意到\(\phi (x) \equiv 0\)是上述方程的平凡解。幸运的是,当\(\lambda\)去某些特殊值时,该方程还有非平凡解。这些\(\lambda\)值称为特征值,对应的非平凡解\(\phi (x)\)称为特征函数。
这部分的详细介绍可以参照笔记“高阶线性微分方程”,这里简述如下:
寻求两个无关解,从指数形式\(\phi = e^{rx}\),得到特征多项式为\(r^2 = -\lambda\)。解的性质与\(\lambda\)取值有关,有4种情况:

暂时忽略第四种情况(第5章会证明)
a. 当\(\lambda >0\)
通解为:
(有时也会选择
)
应用边界条件\(\phi (0) = 0\),得到\(c_1 = 0\)
应用\(\phi (L) = 0\),因此\(0 = c_2 sin(\sqrt{\lambda}L)\). 为了寻找非平凡解,\(c_2 \ne 0\), \(sin(\sqrt{\lambda}L) = 0\)
因此,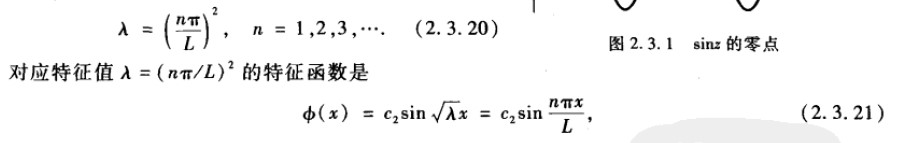
这里c2是任意常数,通常为c2选择一个方便的值,例如1.不过应该记住,任何特定的特征函数总可以用任意常数相乘,因为偏微分方程和边界条件都是线性和齐次的。
b. 当\(\lambda = 0\)
通解为:\(\phi = c_1 + c_2 x\).
为确定\(\lambda = 0\)是否为一个特征值,需要应用齐次边界条件:
\(\phi (0) = 0\),得到\(c_1 = 0\)
\(\phi (L) = 0\),因此\(0 = c_2 L\).因此\(c_2 = 0\)
所以\(\phi = 0\),这是平凡解。因此对于这个问题\(\lambda = 0\)不是特征值。
c. 当\(\lambda < 0\)
特征多项式的根为\(r=\pm \sqrt{-\lambda}\), 通解为
$\phi = c_1 e^\sqrt{(-\lambda)}x + c_2 e^{-\sqrt{(-\lambda)}x} $
经常用双曲函数代替指数函数,双曲函数的定义为:

其函数图像为:
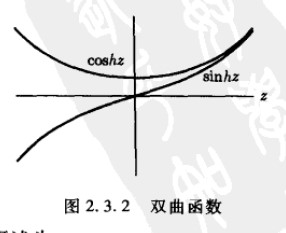
双曲函数的求导公式为:与三角函数类似,但是没有负号
\(\frac{dcosh(z)}{dx} = sinh(z)\), \(\frac{dsinh(z)}{dx} = cosh(z)\)
用双曲函数代替指数函数,通解变为:
\(\phi = c_3 cosh\sqrt{(-\lambda)}x+c_4 sinh\sqrt{(-\lambda)}x\)
为了确定是否存在负特征值,再次使用边界条件。
\(\phi (0) = 0\),得到\(c_3 = 0\)
\(\phi (L) = 0\),因此\(0 = c_4 sinh\sqrt{(-\lambda)}L\)
从双曲图像看出,对一个正变量,sinh不等于0,因此\(c_4 = 0\)
所以,\(\lambda < 0\)不是一个特征值。
(5) 得到乘积解
以上过程求得了\(\phi(x)\)和\(G(t)\),以及对应的特征值,下面可以写出乘积解形式:

(6)叠加原理
如果u1,u2...un是一个齐次线性问题的解,那么这些解的线性组合仍然是该齐次线性方程的解。所以,对任意有限M:

也是热传导方程的解。
对于每个解,振幅\(B_n\)都是不同的。现在考虑初值条件,如果初始条件:
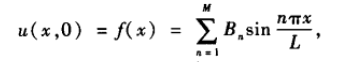
即初始条件为合适的正弦函数的有限和,热传导方程是可以求解的。通常当\(f(x)\)不满足该条件时,傅里叶级数理论指出
\(f(x)\)可以用正弦函数的有限线性组合逼近,且\(M \to \infty\), 无穷级数收敛于\(f(x)\)[对\(f(x)\)有一些限制]
(7)使用初始条件及特征函数正交性确定系数
函数正交性
以向量的观点看待函数,定义
如果\(\int_0^L A(x)B(x)dx = 0\), 则函数\(A(x)\)正交于函数\(B(x)\)。
若一个函数集中的每个元素都与其他元素正交,则称之为正交函数集。
三角函数的正交性
利用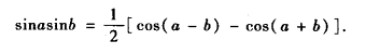
可以计算:
利用:
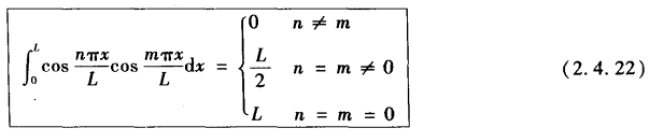
正弦平方或余弦平方在一个全周期内的均值为1/2, 因此在正弦或余弦平方的任意多个全周期内的积分等于该区间长度的一半。
利用奇偶函数特性,可知:(注意积分限的不同)

注意sin,cos的正交区间为[-L,L]. 他们在[0,L]上不是正交的。
确定系数
在初值函数两边乘以\(sin m\pi x/L\),并从0到L积分得:
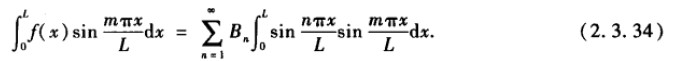
利用正交性:
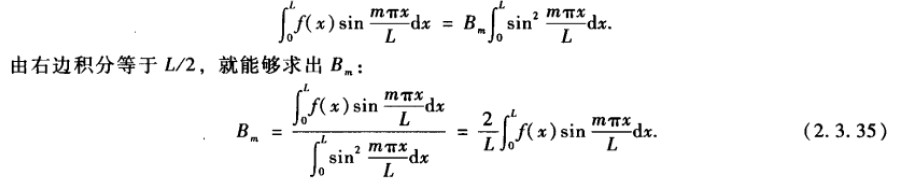
以上就是分离变量法的步骤,应该理解而不是死记硬背。另外需要记住:
- 对偏微分方程的解应用叠加原理,不是累加不同常微分方程的解
- 在使用叠加原理之后再应用初始条件。
5 边值问题小结
在很多问题中,这个具体的简单常系数微分方程
\(\frac{d^2\phi}{dx^2} = -\lambda\)
构成了边值问题的基本部分,现总结如下表。需要注意,在这些情形中,只要\(\lambda = 0\)是特征值,常数就是特征函数(在
\(cosn\pi x/L\)中对应n=0)


6 矩形区域内的拉普拉斯方程
可以看到使用叠加原理将非齐次边界条件转换为齐次边界条件。

为了解决非齐次边界条件,对该非齐次应用叠加原理,令
\(u(x,y) = u_1(x,y) +u_2(x,y)+u_3(x,y)+u_4(x,y)\),其中每个\(u_i(x,y)\)满足一个非齐次边界条件和一个齐次边界条件。如图所示:
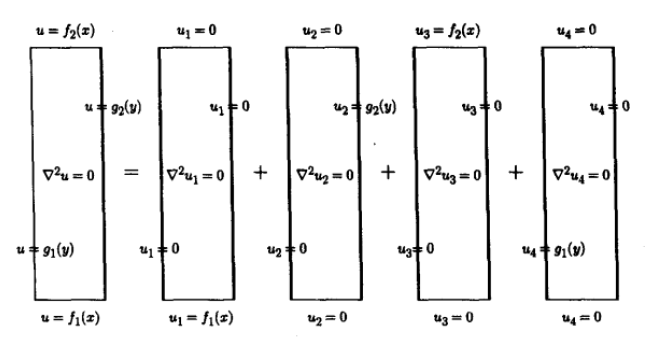
这样只要分别求解\(u_i(x,y)\)即可。以\(u_4(x,y)\)为例,满足下列方程
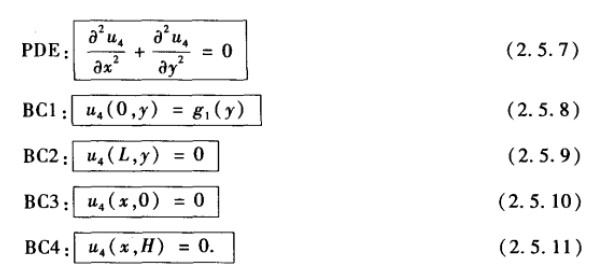
可以看到,关于y的两个边界为齐次边界条件,因此先求解y的,分离变量的:

对比表2.4.1,引入分离变量\(\lambda\)(不是\(-\lambda\)),求解得到:

将\(\lambda\)代入h的方程,得到通解: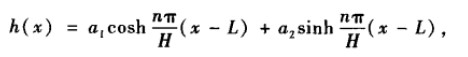
(为了求解齐次边界条件h(L)=0,使用了如下无关解)
由齐次边界条件得到\(a_1 = 0\)
应用叠加原理得到:
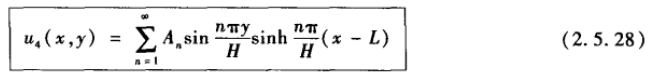
现在由非齐次条件求解系数:
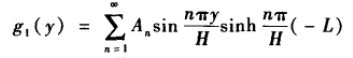
利用正弦函数的正交性可以得到系数公式:
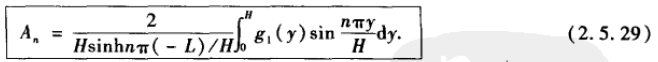
7 圆盘内的拉普拉斯方程
通过物理原因找到边界条件:
通过连续性可得:周期性条件
上面的边界条件中,只有\(u(a,\theta) = f(\theta)\)为非齐次边界条件。 因此该问题适用分离变量法
乘积解形式:\(u(r,\theta) = \phi(\theta)G(r)\)
带入PDE方程,为了能够分离变量,两边同时除以\((1/r^2)\phi(\theta)G(r)\)得到:
\(\frac{r}{G} \frac{d}{dr}(r\frac{dG}{dr})=-\frac{1}{\phi}\frac{d^2\phi}{d\theta^2}=\lambda\)
这是引入分离变量\(\lambda\)(而不是\(-\lambda\)),因为\(\theta\)有两个齐次条件,可以预计在\(\theta\)内震荡。
通过表2.4.1得到特征值,并且对于圆金属丝(\(L=\pi\)):
\(\lambda = (\frac{n\pi}{L})^2=n^2\)
对应的特征函数有两个,即\(sinn\theta\)和\(cosn\theta\)
这时需要注意n=0也要包含在内,对应一个常数特征函数。
以上求解了\(n=0, n \ne 0\)两种情况下的通解。由于\(G(r)\)有界,\(c_2 = 0, \tilde{c_2} = 0\)
最终得到通解为:
\(G(r) = c_1 r^n, n \ge 0\)
因此通过分离变量法得到满足三个齐次条件的乘积解是:
\(r^ncos(n\theta) (n \ge 0)\) 和 \(r^nsin(n\theta) (n \ge 1)\)
应用叠加原理:
从以上可以看到矩形及圆形区域内的拉普拉斯方程求解过程,都是先从齐次条件入手,利用分离变量法求解部分乘积。然后使用非齐次边界条件确定系数,最终得到通解。

