目录如下:
1. 推导一维杆的热传导方程:从微分及积分角度分别进行了推导
2. 初值和边界条件:初值是与时间相关、边值与空间相关
3. 二维及三维热传导方程推导:从积分角度推导,得到泊松方程和拉普拉斯方程
4. 拉普拉斯算子的各种形式:在直角坐标系、柱坐标系和球坐标系下推导拉普拉斯算子形式
偏微分方程(PDE)就是指含有偏导数的数学方程。
本书从物理问题开始研究偏微分方程,便于读者与实际结合。首先讲解的是热传导方程:
1. 推导一维杆的热传导方程
讲解了两种方式:微分的观念,从一个小的薄片的能量守恒推导,通过取极限的方式得到热传导方程


另外一种,从积分角度考虑,利用积分基本定理,这种方式更加精确,避免了极限过程的近似计算。

2. 初值和边界条件:
关于时间变量的称为初值条件,是时间变量的几阶导数就要几个初值条件。
关于空间变量的称为边界条件。
边界条件有三类:
给定温度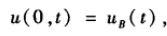
给定温度变化率 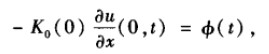
给定温度温度变化率与分布的函数关系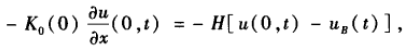
3. 二维及三维热传导方程推导
从积分角度进行推导,根据能量守恒
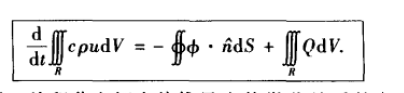
根据高斯定理,把曲面积分转换为三重积分,整理上式得到:(注意把时间作为偏导数放入积分中)

因此:
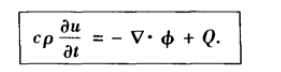
又根据傅里叶导热定律:
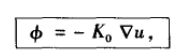

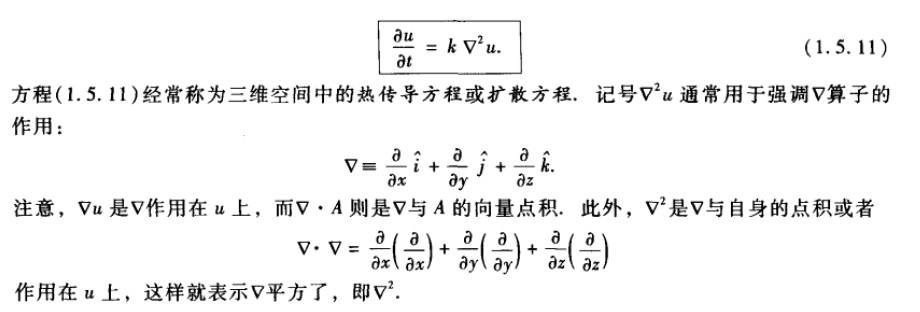
稳态:如果边界条件和热源都与时间无关,在恒定热性质的情形,平衡温度分布将满足:
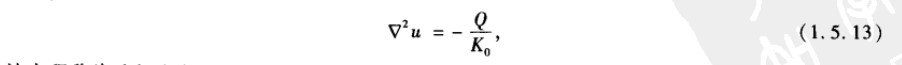
该方程称为泊松方程。
如果热源不存在,泊松方程变为:
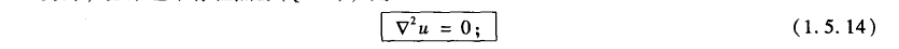
即温度分布的拉普拉斯算子是零,因此称为拉普拉斯方程。
二维方程的推导与三维一致,只是使用面积分代替体积分,使用格林公式代替高斯公式。
4. 拉普拉斯算子的各种形式
在直角坐标系下:

在柱面坐标系下有:

下面证明在柱面坐标系下的拉普拉斯公式:
考虑二维下的柱面坐标,即极坐标:
可以证明:

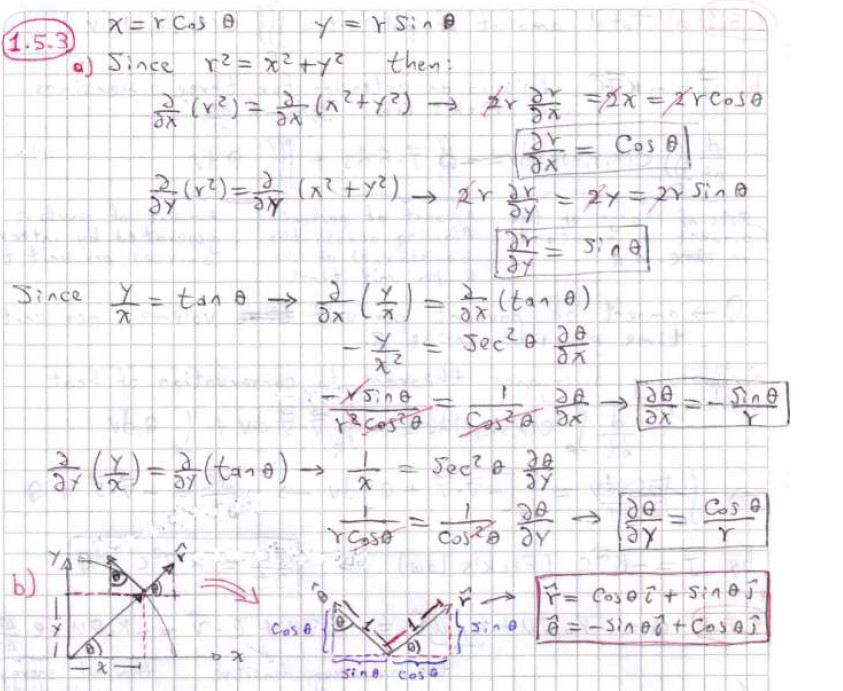
利用链式法则:

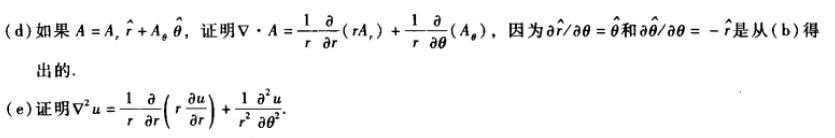


以上可以得到柱坐标下的拉普拉斯算子公式:
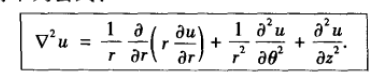
在这个公式中,需要注意的是:在拉普拉斯算子中的每一项都有u的量纲被两个空间量纲除。因为角度是用弧度测量的,没有
量纲,因此,对角度的微分需要除以半径的平方。
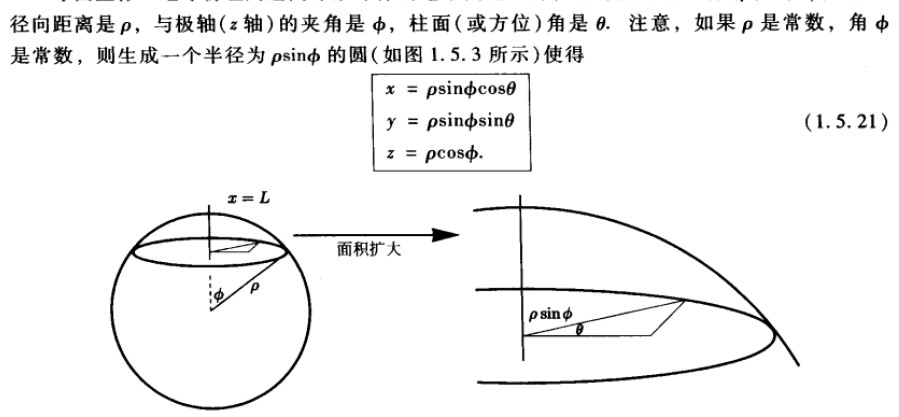
通过以上思路可以证明球坐标的公式:
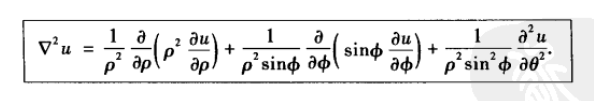
<wiz_tmp_tag id="wiz-table-range-border" contenteditable="false" style="display: none;">



