高阶线性微分方程-常微分方程

这里讨论常微分方程。常微分方程的阶数就是函数求导的最高次数。这里以二阶线性微分方程为例。

形如方程5的称为二阶线性微分方程。

 

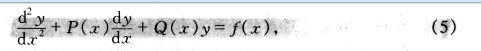
线性的概念定义为：

 

下面讨论 二阶线性微分方程，这些性质也可以推广到n阶线性方程：

 

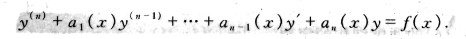
1. 线性微分方程的解的结构

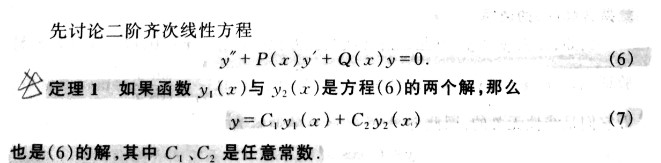
 目前，式（7）不是（6）的通解。如何保证通解呢，首先引入函数组线性无关的概念：

 

 

下面讨论二阶非齐次线性方程，非齐次方程的解是齐次方程的通解加上非齐次方程的一个特解构成的。

 非齐次方程的特解可以使用下述定理帮忙求出：

 这一定理称为线性微分方程的解的叠加原理。

以上研究的是高阶线性微分方程的解的结构，下面介绍解法，首先讨论二阶常系数齐次线性微分方程的解法

然后把二阶方程的解法推广到n阶方程。

首先使用y=exp(rx)得到该方程的特征方程，然后根据特征方程解的形式进行讨论。

（1）特征方程有两个不相等实根，则y1,y2不相关，根据定理2，得到通解

（2）特征方程有两个相等实根，则需要找到另外一个不相关的y2

（3）特征方程有一对共轭复根，则利用欧拉公式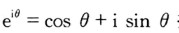（）及叠加原理将复值函数转变为实值函数。

从而求得不相关的函数，得到通解。

推导过程见下图：

 

总结如下：

 

将以上结论推广到n阶常系数齐次线性微分方程。