平衡二叉树

平衡二叉树

1.基本介绍

1）平衡二叉树也叫平衡二叉搜索树，又被称为AVL树，可以保证查询效率查询。

2）特点：它是一颗空树或它的左右子树的高度差的绝对值不超过1，并且左右两个子树都是平衡二叉树。

平衡二叉树的实现方法：红黑树、AVL、替罪羊树、Treap、伸展树等。

2.平衡二叉树左旋转

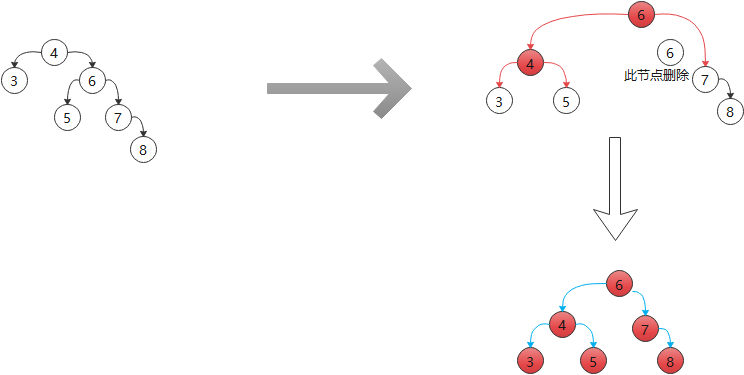
1）使用数列{4，3，6，5，7，8}，当插入8时，rightHeight（根节点的右子树的高度） - leftHeight（根节点的左子树的高度） > 1,此时就需要左旋转。

左旋转的思路：

① 创建一个新的结点，值等于当前根节点的值（在这题中为4）。

② 把新结点的左子树设置为当前结点左子树。

③ 把新结点的右子树设置为当前结点的右子树的左子树。

④ 把当前结点的值设置为右子结点的值。

⑤ 把当前结点的右子树设置为当前结点的右子树的右子树。

⑥ 把当前结点的左子树设置为新的结点。

3.平衡二叉树右旋转

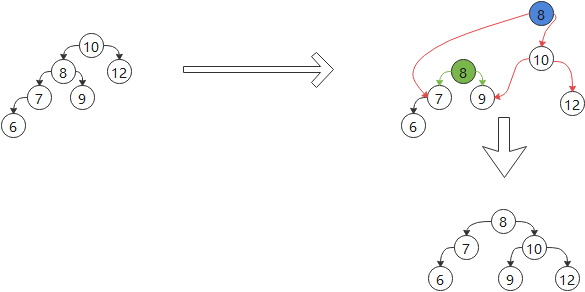
1）使用数列{10，12，8，9，7，6}，当插入6时， leftHeight（根节点的左子树的高度） - rightHeight（根节点的右子树的高度） > 1,此时就需要右旋转。

左旋转的思路：

① 创建一个新的结点，值等于当前根节点的值（在这题中为10）。

② 把新结点的右子树设置为当前结点右子树。

③ 把新结点的左子树设置为当前结点的左子树的右子树。

④ 把当前结点的值设置为左子结点的值。

⑤ 把当前结点的左子树设置为当前结点的左子树的左子树。

⑥ 把当前结点的右子树设置为新的结点。

package com.sratct.tree;

import java.util.LinkedList;

public class AVLTreeDemo {
    public static void main(String[] args) {
//        int[] arr = {4, 3, 6, 5, 7, 8};
//        int[] arr = {10, 12, 8, 9, 7, 6};
//        int[] arr = {10, 7, 11, 6, 8, 9};
        int[] arr = {7, 6, 10, 8, 11, 9};
        AvlNode avlNode = new AvlNode(arr[0]);
        for (int i = 1; i < arr.length; i++) {
            add(avlNode, new AvlNode(arr[i]));
        }
//        System.out.println(treeHeight(avlNode));
//        System.out.println(LHeight(avlNode));
//        System.out.println(RHeight(avlNode));
        cList(avlNode);
    }

    // 求左子树的高度
    public static int LHeight(AvlNode root) {
        if (root.left == null) {
            return 0;
        }
        return treeHeight(root.left);
    }

    // 求右子树的高度
    public static int RHeight(AvlNode root) {
        if (root.right == null) {
            return 0;
        }
        return treeHeight(root.right);
    }
    // 求树的高度
    public static int treeHeight(AvlNode root) {
        if (root == null) {
            return 0;
        }
        int lMax = 0; // 左子树的高度
        int rMax = 0; //右子树的高度
        if (root.left != null) {
            lMax = treeHeight(root.left);
        }
        if (root.right != null) {
            rMax = treeHeight(root.right);
        }

        return lMax > rMax ? lMax + 1 : rMax + 1;
    }

    /**
     * 左旋转树
     * @param root
     */
    public static void leftRotate(AvlNode root) {
        if (root == null) {
            return;
        }
        // 1.创建一个新结点，赋值为当前结点
        AvlNode newNode = new AvlNode(root.no);
        //2.让新结点的左子结点等于当前节点的左子树
        if (root.left != null) {
            newNode.left = root.left;
        }
        // 3.让新结点的右子节点等于当前结点的右子节点的左子节点
        newNode.right = root.right.left;
        // 4.让当前结点的值等于右子节点的值
        root.no = root.right.no;
        // 5.让当前结点右子节点等于当前节点的右子节点的右子结点
        root.right = root.right.right;
        // 6.当前节点的左子节点等于新结点
        root.left = newNode;
    }

    /**
     * 右旋转
     * @param root
     */
    public static void rightRotate(AvlNode root) {
        if (root == null) {
            return;
        }
        // 创建一个新结点，值等于当前结点的值
        AvlNode newNode = new AvlNode(root.no);
        // 让新结点的右子树等于当前结点的右子树
        newNode.right = root.right;
        // 让新结点的左子树等于当前结点的左子树的左右子树
        newNode.left = root.left.right;
        // 让当前结点的值等于左子节点的值
        root.no = root.left.no;
        // 让当前结点的左子树等于当前结点的左子树的左子树
        root.left = root.left.left;
        // 让当前结点的右子树等于新结点
        root.right = newNode;
    }
    // 添加元素
    public static void add(AvlNode root, AvlNode node) {
        if (node == null) {
            return;
        }
        if (root == null) {
            root = node;
            return;
        }
        // 判断插入结点的和当前结点的大小
        if (node.no < root.no) {
            // 小于，判断左子节点是否为空
            if (root.left == null) {
                root.left = node;
            } else {
                add(root.left, node);
            }
        } else {
            // 大于，判断右子节是否为空
            if (root.right == null) {
                root.right = node;
            } else {
                add(root.right, node);
            }
        }

        // 判断当前是否为平衡二叉树
        //如果(右子树高度 - 左子树高度>1):左旋转
        if (RHeight(root) - LHeight(root) > 1) {
            // 判断是否需要双旋转即，判断当前节点的右结点的左子树高度是否大于当前节点的右结点的右子树高度
            if (root.right != null && (LHeight(root.right) > RHeight(root.right))) {
                // 大于，则先对当前结点的右子树进行右旋转
                rightRotate(root.right);
                // 再对当前结点进行左旋转
                leftRotate(root);
            } else {
                // 直接进行左旋转
                leftRotate(root);
            }
            return;
        }
        // 如果(左子树的高度 - 右子树的高度 > 1):右旋转
        if (LHeight(root) - RHeight(root) > 1) {
            // 判断是否需要双旋转，即：判断当前结点的左节点的右子树高度是否大于当前节点的左节点的左子树高度
            if (root.left != null && (RHeight(root.left) > LHeight(root.left))) {
                // 大于，先对当前结点的左子树进行左旋转
                leftRotate(root.left);
                // 再进行右旋转
                rightRotate(root);
            } else {
                // 直接右旋转
                rightRotate(root);
            }
        }
    }

    /**
     * 层序遍历
     *
     * @param root
     */
    public static void cList(AvlNode root) {
        LinkedList<AvlNode> nodes = new LinkedList<>();
        if (root == null) {
            return;
        }
        nodes.offer(root);
        while (!nodes.isEmpty()) {
            AvlNode poll = nodes.poll();
            System.out.println(poll.no);
            if (poll.left != null) {
                nodes.offer(poll.left);
            }
            if (poll.right != null) {
                nodes.offer(poll.right);
            }
        }
    }
}

class AvlNode {
    public int no;
    public AvlNode left;
    public AvlNode right;

    public AvlNode(int no) {
        this.no = no;
    }
}