二叉树

二叉树

1.概念

1）每个结点最多只能有两个子节点的一种形式称为二叉树

2）二叉树的子节点分为左节点和右节点。

3）如果该二叉树的所有叶子节点都在最后一层，并且结点总数=2^n - 1,n为层数，则成为满二叉树。

4）如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层叶子节点在左边连续，倒数第二层叶子结点在右边连续，我们称为完全二叉树。

2.二叉树的遍历

前序遍历：根结点、左子树、右子树；

中序遍历：左子树、根节点、右子树；

后序遍历：左子树、右子树、根节点；

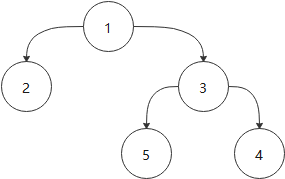
层序遍历：从上往下，从左往右一次遍历

  遍历思路：首先创建一个辅助队列，让根节点E入队，判断E是否有左右子树，有则入队，一次类推，直到找完。如下图：

3.二叉树的查找

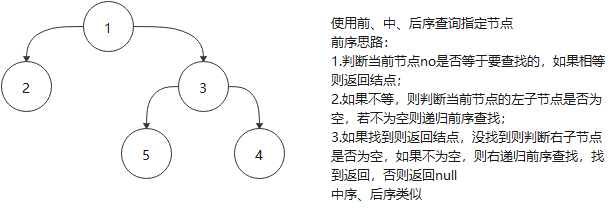
代码

package com.sratct.tree;

import jdk.nashorn.internal.ir.IfNode;

public class BinaryTreeDemo {
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        Node node = new Node(1);
        Node node1 = new Node(2);
        Node node2 = new Node(3);
        Node node3 = new Node(4);
        Node node4 = new Node(5);
        node.left = node1;
        node.right = node2;
        node2.left = node4;
        node2.right = node3;
        Node node5 = binaryTree.qSearch(node, 6);
    if (node5 != null) {
        System.out.println(node5.no);
    } else {
        System.out.println("未找到");
    }

    }
}
class BinaryTree{
    // 前序遍历
     public void qList(Node root) {
         if (root!=null) {
             System.out.println(root.no);
             if (root.left != null) {
                 qList(root.left);
             }
             if (root.right != null) {
                 qList(root.right);
             }
         } else {
             System.out.println("二叉树为空");
         }
     }
    // 中序遍历
    public void zList(Node root) {
        if (root != null) {
            if (root.left != null) {
                zList(root.left);
            }
            System.out.println(root.no);
            if (root.right != null) {
                zList(root.right);
            }
        } else {
            System.out.println("二叉树为空");
        }
    }
    // 后序遍历
    public void hList(Node root) {
        if (root != null) {
            if (root.left != null) {
                hList(root.left);
            }
            if (root.right != null) {
                hList(root.right);
            }

            System.out.println(root.no);
        } else {
            System.out.println("二叉树为空");
        }
    }
 /**
     *  层序遍历
     *
     */
    public void cList(Node root) {
        LinkedList<Node> nodes = new LinkedList<>();
        // 根节点入队
        nodes.offer(root);
        Node cur = null;
        while (!nodes.isEmpty()) {
            // 结点出队
            Node poll = nodes.poll();
            System.out.println(poll.no);
            // 判断该结点的左子节点是否为null,不为null则入队
            if (poll.left != null) {
                nodes.offer(poll.left);
            }
            // 判断该结点的右子节点是否为null,不为null则入队
            if (poll.right != null) {
                nodes.offer(poll.right);
            }
        }
    }
    // 前序查找
    public Node qSearch(Node root, int no) {
         // 如果等于当前结点则返回
         if (root.no == no) {
             return root;
         }
         // 左递归
        Node lResult = null;
        if (root.left != null) {
            lResult = qSearch(root.left, no);
        }
         if (lResult != null) {  // 不为null则返回
             return lResult;
         }
         // 右递归
         if (root.right != null) {
             return qSearch(root.right,no);
         }
         return null;
    }

    // 中序查找
    public Node zSearch(Node root, int no) {
       Node lNode = null;
         if (root.left != null) {
             lNode = zSearch(root.left, no);
         }
         if (lNode != null) {
             return lNode;
         }
         if (root.no == no) {
             return root;
         }
         if (root.right != null) {
             return zSearch(root.right, no);
         }
         return null;
    }

    // 后续遍历
    public Node hSearch(Node root, int no) {
         Node lNode = null;
         if (root.left != null) {
             lNode = hSearch(root.left,no);
         }
         if (lNode != null) {
             return lNode;
         }
         Node rNode = null;
         if (root.right != null) {
             rNode = hSearch(root.right, no);
         }
         if (rNode != null) {
             return rNode;
         }
         if (root.no == no) {
             return root;
         }
         return null;
    }
}
// 创建结点
class Node{
    public int no;
    public Node left;
    public Node right;

    public Node(int no) {
        this.no = no;
    }
}