折纸问题

1.问题叙述

 

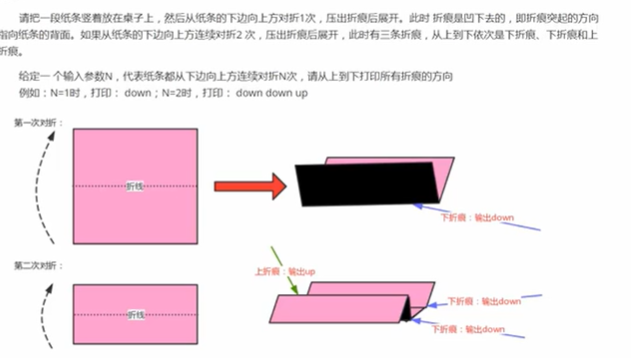
2.分析：

           将对折后的纸翻过来，第一次对折产生的折痕为根节点，第二次对折产生的下折痕为为该节点的左子节点，上折痕为右子节点。

           所有得出结论：1.根节点为下折痕

                                     2.每个节点的左子节点为上折痕

                                     3.每个节点的右子节点为下折痕

 

public class PageTest{
    public static void main(String[] args) {
      Node<String> tree =creatTree(3);
      //打印树
        printTree(tree);
    }
    //通过模拟对折n次产生树
    public static Node<String> creatTree(int N){
        //定义根节点
        Node<String> root=null;
        for (int i=0;i<N;i++){
            //1.第一次对折
            if (i==0){
                root=new Node<>("down",null,null);
                continue;
            }
            //2.当前不时第一次对折
             //定义一个辅助队列，利用层次遍历的思想，找到叶子节点，添加节点
            Queue<Node> queue=new Queue<>();
            queue.insert(root);
            //循环遍历队列
            while (!queue.isEmpty()){
                //从队列中出一个节点
                Node<String> temp = queue.remove();
                //如果该节点的左子节点不为空，则把他的左子节点放入队列
                if (temp.left!=null){
                    queue.insert(temp.left);
                }
                //如果该节点的右子节点不为空，则把他的右子节点放入队列
                if (temp.right!=null){
                    queue.insert(temp.right);
                }
                //如果该节点的左右字节点都为空时，则创建左右字节点
                if (temp.left==null && temp.right==null){
                    temp.left=new Node<String>("down",null,null);
                    temp.right=new Node<String>("up",null,null);
                }

            }
        }
        return root;
    }
    //打印树中每个节点
    public static void printTree(Node<String> root){
           //使用中序遍历
        if(root==null){
            return;
        }
        //打印左子树每个节点
        if (root.left!=null){
            printTree(root.left);
        }
        //打印根节点
        System.out.print(root.item+" ");
        //打印右子树每个节点
        if (root.right!=null){
            printTree(root.right);
        }
    }
    private static class Node<T> {
        T item;
        Node left;
        Node right;
        public Node(T item, Node left, Node right) {
            this.item = item;
            this.left = left;
            this.right = right;
        }
    }

}