二叉树
一、树
1.定义:树是由n(n>=1)个有限结点组成一个具有层次关系的集合
2.特点:1)每个结点有零个或多个子结点
2)没有父结点的为根结点
3)每一个非根结点只有一个父结点
3.树的相关术语
1)结点的度:一个结点的子结点个数
2)叶节点:度为零的结点,也叫终端结点
3)结点的层次:从根结点开始为1,一次往下为2....
4)树的度:树中所有结点的度的最大值
5)树的高度:树中结点的最大层次
二、二叉树
1.定义:二叉树是指度不超过二的树。
2.满二叉树:一个二叉树,每一层的结点都达到最大值,每一层节点最大值为2的k-1次方
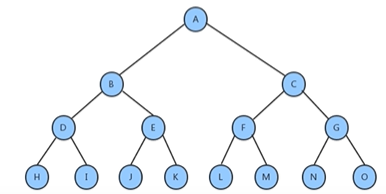
3.完全二叉树:叶结点只能出现在下层或者次下层,并且最下层的结点都集中在该层的左边
4.二叉查找树的基本实现
1)插入:如果当前树中没有节点,则直接把新结点作为根节点
如果树不为空,则从根节点开始:如果新结点的key小于当前节点的key,则继续找当前节点的左子节点(递归)
如果新结点的key大于当前节点的key,则继续找当前节点的右子节点(递归)
2)查找:从根节点开始
如果查询的key小于当前节点的key,则继续找当前节点的左子节点(递归)
如果查询的key大于当前节点的key,则继续找当前节点的右子节点(递归)
如果查询的key等于于当前节点的key,则直接返回当前的value
3)删除:* 先找到删除的节点
* 找到要删除的节点的右子树中的最小节点minNode,记录此节点并删除
* 然后让最小的节点minNode指向被删除节点的左子树和右子树,再让被删除的节点的父节点指向最小节点minNode
4) 输出最小键:从根节点开始一直遍历左子树,直到没有左子树时输出当前节点的key,此结点的key为最小键
5)输出最大键:从根节点开始一直遍历右子树,直到没有右子树时输出当前节点的key,此结点的key为最大键
6)先序遍历: 先访问根节点,再访问左子树,最后访问右子树。
核心实现步骤:* 把根节点放入队列,队列的创建:https://www.cnblogs.com/cqyp/p/12576340.html
* 递归遍历左子树
* 递归遍历右子树
7)中序遍历:先访问左子树,再访问根节点,最后访问右子树。
8)后续遍历:先访问左子树,再访问右子树,最后访问根节点。
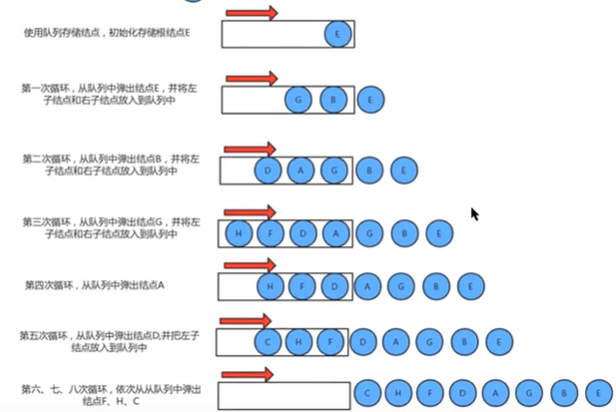
9)层序遍历:从上往下,从左往右一次遍历
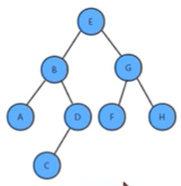
遍历思路:首先创建一个辅助队列,让根节点E入队,判断E是否有左右子树,有则入队,一次类推,直到找完。如下图:
10)最大深度
递归遍历左子树和右子树,求出左右子树的深度,然后比较,大的加一则为树的深度。
public class BinaryTree<Key extends Comparable<Key>,Value> { //根节点 private Node root; //树的个数 private int N; public class Node{ //存储的键 public Key key; //存储的值 public Value value; //记录左子节点 public Node left; //记录右子节点 public Node right; public Node(Key key, Value value, Node left, Node right) { this.key = key; this.value = value; this.left = left; this.right = right; } } public BinaryTree() { this.root=null; this.N=0; } //获取树中的个数 public int size(){ return N; } //向树中添加一个元素key-value public void put(Key key,Value value){ root=put(root,key,value); } //向指定的树x中添加一个元素key-value,并返回添加后的树 public Node put(Node x,Key key,Value value){ //如果x的子树为空 if (x==null){ N++; return new Node(key, value, null, null); } //如果子树不为空 //比较x.key和key的大小 int cmp=key.compareTo(x.key); //如果大于0,则继续找x的右子树 if(cmp>0){ x.right=put(x.right,key,value); } //如果小于0,则继续找x的左子树 if (cmp<0){ x.left=put(x.left,key,value); }else{ //如果相等,则将此结点的value替换 x.value=value; } N++; return x; } //查询树中指定key对应的value public Value get(Key key){ return get(root,key); } //从指定的树x中查找key对应的值 public Value get(Node x,Key key){ //如果x为null if (x==null){ return null; } //如果x不为null //比较x.key和key的大小 int cmp=key.compareTo(x.key); //如果大于0,则继续找x的右子树 if(cmp>0){ return get(x.right,key); } //如果小于0,则继续找x的左子树 if (cmp<0){ return get(x.left,key); }else{ //如果相等,则找到 return x.value; } } //删除树中key对应的value值 public void delete(Key key){ root=delete(root,key); } //删除指定树x中的key对应的value,并返回删除后的新树 public Node delete(Node x,Key key){ if (x==null){ return null; } //如果不为null //比较x.key和key的大小 int cmp=key.compareTo(x.key); //如果大于0,则继续找x的右子树 if(cmp>0){ x.right=delete(x.right,key); } //如果小于0,则继续找x的左子树 if (cmp<0){ x.left=delete(x.left,key); }else{ N--; //如果相等,则找到,删除x //找到右子树最小的节点 //1.如果x的右子树为空,直接返回左子树不用找最小 if (x.right==null){ return x.left; } //2.如果x的左子树为空,直接返回右子树,不用找最小 if (x.left==null){ return x.right; } //3.如果左右子树都不为空,找最小节点 Node minNode=x.right; while (minNode.left!=null){ minNode=minNode.left; } //删除右子树的最小节点 // Node n=x.right; while (n.left!=null){ if (n.left.left==null){ n.left=null; }else{ n=n.left; } } //让x的左子树成为minNode的左子树 minNode.left=x.left; //让x的右子树成为minNode的右子树 minNode.right=x.right; //让x的父节点指向minNode x=minNode; } return x; } //查找整个树中最小的键 public Key min(){ return min(root).key; } //在指定树x中找出最小键所在的节点 public Node min(Node x){ //判断x的左子节点是否为空 if (x.left!=null){ return min(x.left); }else{ return x; } } //查找整个树中最大的键 public Key max(){ return max(root).key; } //在指定树x中找出最大键所在的节点 public Node max(Node x){ //判断x的右子节点是否为空 if (x.right!=null){ return max(x.right); }else{ return x; } } //先序遍历 public Queue<Key> preErgodic(){ Queue<Key> keys=new Queue<>(); preErgodic(root,keys); return keys; } public void preErgodic(Node x,Queue<Key> keys){ //判断x是否为null if(x==null){ return; } //把x节点的key放到队列中 keys.insert(x.key); //把x的左子树递归放到队列中 if(x.left!=null){ preErgodic(x.left,keys); } //把x的右子树递归放到队列中 if(x.right!=null){ preErgodic(x.right,keys); } } //中序遍历 public Queue<Key> midErgodic(){ Queue<Key> keys=new Queue<>(); midErgodic(root,keys); return keys; } public void midErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } //递归遍历左子树并放到队列中 if(x.left!=null){ midErgodic(x.left,keys); } //把x放到对列中 keys.insert(x.key); //把x的右子树递归放到队列中 if(x.right!=null){ midErgodic(x.right,keys); } } //后序遍历 public Queue<Key> hErgodic(){ Queue<Key> keys=new Queue<>(); hErgodic(root,keys); return keys; } public void hErgodic(Node x,Queue<Key> keys){ if (x==null){ return; } //递归遍历左子树并放到队列中 if(x.left!=null){ hErgodic(x.left,keys); } //把x的右子树递归放到队列中 if(x.right!=null){ hErgodic(x.right,keys); } //把x放到对列中 keys.insert(x.key); } //使用层次遍历 public Queue<Key> layerErgodic(){ //定义两个队列,分别存储节点和key值 Queue<Node> nodes = new Queue<>(); Queue<Key> keys=new Queue<>(); //先把根节点放入队列nodes中 nodes.insert(root); //当nodes队列不为null时从中弹出节点 while (!nodes.isEmpty()){ Node n = nodes.remove(); keys.insert(n.key); //判断节点是否有左子节点,有,则进入nodes的队列 if (n.left!=null){ nodes.insert(n.left); } //判断节点是否有右子节点,有,则进入keys的队列 if (n.right!=null){ nodes.insert(n.right); } } return keys; } //最大深度 public int maxDepth(){ return maxDepth(root); } public int maxDepth(Node x){ if (x==null){ return 0; } //树的最大深度 int max=0; //左子树最大深度 int maxL=0; //右子树最大深度 int maxR=0; //计算左子树的最大深度 if (x.left!=null){ maxL=maxDepth(x.left); } //计算右子树的最大深度 if (x.right!=null){ maxR=maxDepth(x.right); } //比较左右子树的深度大小,大的加1则为树的最大深度 max=maxL>maxR ? maxL+1 : maxR+1; return max; } }

