高级排序
一、希尔排序（对插入排序进行优化）
原理：1.选定一个增长量h,按h作为分组依据，对数据进行分组
2.对分好组的每一组进行插入排序
3.减少增长量，最少减为一，重复第二步操作
public class SeniorSort { public static void main(String[] args) { int[] arr = {8,9,1,7,2,3,5,4,6,0}; shellSort2(arr); System.out.println(Arrays.toString(arr)); } /** * 交换式希尔排序 * @param arr */ private static void shellSort(int[] arr) { for (int h = arr.length/2; h>0;h/=2) { // int h = 5; int temp = 0; for (int i = h; i < arr.length; i++) { for (int j = i - h; j >=0; j -= h) { if (arr[j] > arr[j + h]) { temp = arr[j]; arr[j] = arr[j + h]; arr[j + h] = temp; } } } } } /** * 移动法希尔排序 */ public static void shellSort2(int[] arr) { // 增量h,并逐渐缩小 for (int h = arr.length/2;h>0; h/=2) { // 从第h个元素，逐个对其所在的组进行直接插入排序，每组元素之间相差h for (int i=h;i<arr.length;i++) { int j = i; // 当前元素下标 int temp = arr[j]; // 将当前元素暂存起来 // 同一组中，当前元素小于前一个元素 while (j-h>=0 && temp < arr[j-h]) { arr[j] = arr[j-h]; // 将前一个元素向后移动 j = j-h; // 下标前移动 } arr[j] = temp; // 循环结束后，将temp插入到该位置 } } } }
二、归并排序
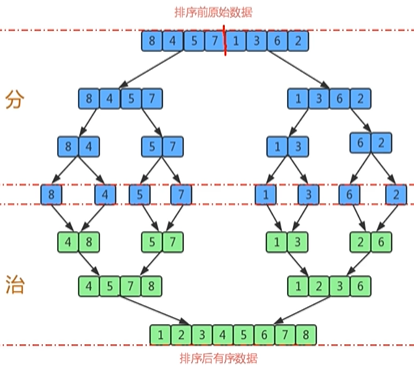
原理：1. 尽可能的一组数据拆分为相等的两份，并对每一个自组继续进行拆分，直到拆分后每个自组的元素个数为1；
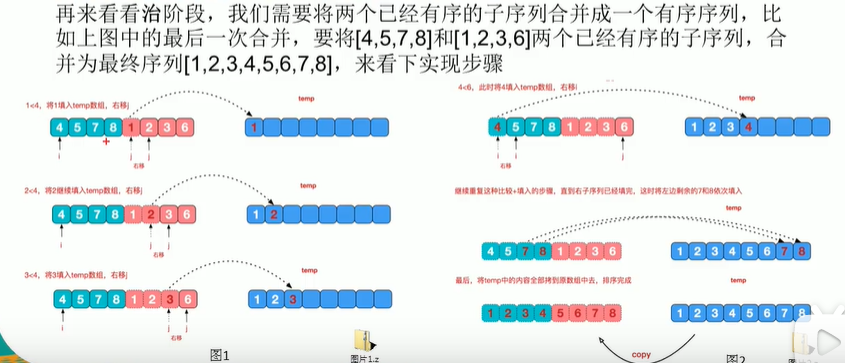
2. 将两个自组合并成一个有序的大组
3.不断重复步骤2，直到成为一个大组
package com.sratct.sort; import java.util.Arrays; /** * 归并排序 */ public class mergerSort { public static void main(String[] args) { int[] arr = {8, 4, 5, 7, 1, 3, 6, 2}; int[] temp = new int[arr.length]; branch(arr,0,arr.length-1,temp); System.out.println(Arrays.toString(arr)); } /** * * @param arr 原始数组 * @param left 原始数组的左边索引 * @param right 原始数组的右边索引 * @param temp 中间暂存数组 */ public static void branch(int[] arr, int left, int right, int[] temp) { if (left < right) { // 找到原始数组的中间索引 int mid = (left + right) / 2; // 左边递归分解 branch(arr,left,mid,temp); // 右边递归分解 branch(arr,mid+1,right,temp); // 分解完成之后进行合并 merger(arr,left,mid,right,temp); } } /** * * @param arr 原始数组 * @param left 原始数组最左边的起始索引 * @param mid 原始数组的中间索引 * @param right 最右边索引 * @param temp 中间暂存数组 */ public static void merger(int[] arr, int left, int mid, int right, int[] temp) { int l = left; // 左边有序序列初始索引 int j = mid + 1; // 右边有序序列的初始索引 int t = 0; //中间暂存数组的初始索引 // 将左边的序列和右边的序列合并到temp中 while (l<=mid && j<=right) { // 如果左边小于右边，将左边的数放到temp中 if (arr[l] < arr[j]) { temp[t] = arr[l]; t++; l++; } else { temp[t] = arr[j]; t++; j++; } } // 如果左边的未合并完，则将左边的一次拷贝到temp中 while (l <= mid) { temp[t] = arr[l]; t++; l++; } // 如果右边的未合并完，则将右边的一次拷贝到temp中 while (j <= right) { temp[t] = arr[j]; t++; j++; } /** * 合并完成之后，将temp中数拷贝到arr中 * 每合并一次，拷贝一次 */ t = 0; int tempLeft = left; while (tempLeft <= right) { arr[tempLeft] = temp[t]; t++; tempLeft++; } } }
三、快速排序
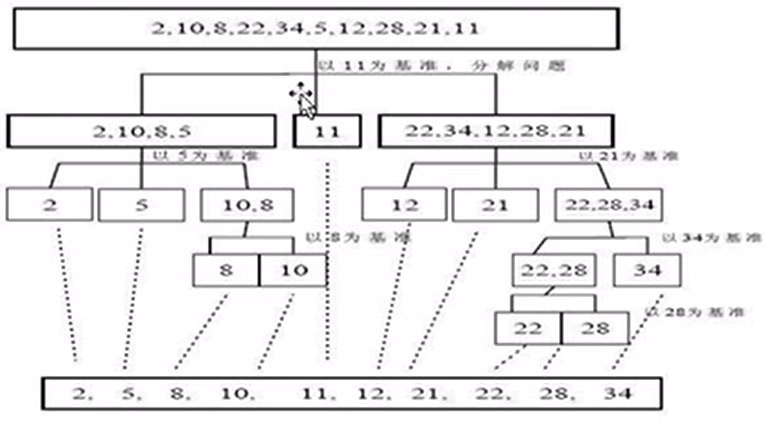
1.快速排序是对冒泡排序的一种改进；
基本思想：通过一趟排序将要排序的数据分割为独立的两部分，一部分 的数据小于另一部分，然后再使用此方法对这两部分进行快速排序，整个过程使用递归进行；
package com.sratct.sort; import java.util.Arrays; /** * 快速排序 */ public class quickSort { public static void main(String[] args) { int[] arr = {-5,5,6,10,50,0,-7,-8,31,12}; // int[] arr = {-9,78,0,23,-567,70}; quickSort(arr,0,arr.length-1); System.out.println(Arrays.toString(arr)); } public static void quickSort(int[] arr,int left,int right) { int l = left; int r = right; int mid = arr[(left + right)/2]; // 以中间值为基准，把小于mid的数放到左边，大于mid的数放到右边 int temp = 0; while (l < r) { // 循环在mid的左边找出大于它的数 while (arr[l] < mid) { l++; } //循环在mid的右边找出小于它的数 while (arr[r] > mid) { r--; } // 当下标l>=r退出 if (l>=r) { break; } //将找出的两个数交换 temp = arr[l]; arr[l] = arr[r]; arr[r] = temp; // 交换后，当arr[l]==mid,r-- if (arr[l] == mid) { r--; } //交换后，当arr[r] == mid,l++ if (arr[r] == mid) { l++; } } if (l == r) { l++; r--; } // 左递归 if (left < r) { quickSort(arr,left,r); } if (right > l) { quickSort(arr,l,right); } } }
四、基数排序
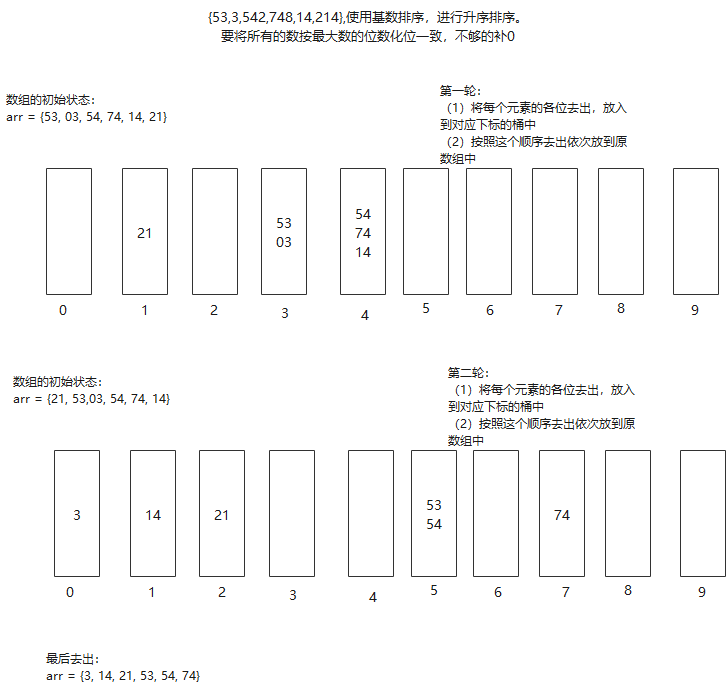
1）基数排序又称‘桶排序’，又称‘桶子法’或bin sort, 他们通过键值各个位置，将要排序的元素分配到某些桶中，达到排序的作用。
2）效率高稳定的排序法
3）是桶排序的扩展
4）将整数按位切成不同的数字，然后按每个位进行比较
基本思想： 将所有带比较的数值统一为同样的位数长度，数位较短的位数前面补0，然后从位数最低位开始排序，这样从最低为到最高位依次排序完成后，就会成为有序的数列。
package com.sratct.sort; import java.util.Arrays; /** * 基数排序 */ public class RadixSort { public static void main(String[] args) { int [] arr = {53, 3, 542, 748, 14, 214}; radixSort(arr); System.out.println(Arrays.toString(arr)); } public static void radixSort (int[] arr) { // 得到数组中最大值 int max = arr[0]; for (int i = 1; i<arr.length;i++) { if (max < arr[i]) { max = arr[i]; } } // 求出最大数值的长度 int maxLength = (max + "").length(); /** * 定义一个二位数组，即十个一维数组作为桶； * 为了防止桶中元素溢出，将每个桶定义为原数组最大长度 */ int[][] buckets = new int[10][arr.length]; // 定义一个一维数组，存放每个桶中存放元素的数量 int[] bucketNums = new int[10]; for (int i=0,n=1;i<maxLength;i++,n*=10) { // 需要进行maxLength轮 // 将原数组中元素按位数放到桶中 for (int j = 0; j < arr.length; j++) { int digitOfElement = arr[j] / n % 10; // 如果为三位数，第一轮为个位，第二轮为十位，第三轮为百位... // bucketNums[digitOfElement]为该值在该桶中存放元素的值，初始值为0 buckets[digitOfElement][bucketNums[digitOfElement]] = arr[j]; // 将元素存放到桶对应下标的位置中， // 存放后，加1 bucketNums[digitOfElement]++; } // 将桶中元素按顺序依次取出，放到原数组中去； int index = 0; for (int k = 0; k < buckets.length; k++) { // 需要判断当前桶中元素个数是否为0，若为0，就不用遍历取值； if (bucketNums[k] != 0) { for (int l = 0; l < bucketNums[k]; l++) { arr[index++] = buckets[k][l]; } } bucketNums[k] = 0; // 当每轮桶中元素取出之后需要将桶中总数清零。 } } } }
五、排序的稳定性
1.定义：假设数组a中右若干元素，其中A和B相等，在A在B的前面，在排完序之后任能保证A在B的前面，则稳定
2.常见排序算法的稳定性
稳定的：冒泡、插入、归并
不稳定的：选择、希尔、快速
