加密算法学习总结---DES-CBC加密算法 & 分组加密的四种模式
加密算法学习总结---DES-CBC加密算法
转载自:https://blog.csdn.net/jdhellfire/article/details/79680456
DES-CBC机密算法
DES全称为Data Encryption Standard,即数据加密标准,是一种使用密钥加密的块算法,1977年被美国联邦政府的国家标准局确定为联邦资料处理标准(FIPS),并授权在非密级政府通信中使用,随后该算法在国际上广泛流传开来。
一.核心原理原理XOR
DES的核心原理是基于XOR数学运算。我们知道异或运算的一个基本性质 A XOR B = C ;C XOR B =A。这个特性和加解密过程非常相似 A用秘钥B加密加密得到C ,C用秘钥B解密得到A。
二.DES的两重迭代
DES是基于数据块的加密。它将待加密数据以64bit为单位拆分为若干数据块。然后再进行两重迭代:
外层迭代是数据块之间的迭代,迭代的方式有ECB、CBC等,本文重点介绍CBC。
内层迭代是通过Feistel网络来实现。
2.1CBC迭代

基于CBC的数据块的加密和解密迭代过程如上图所示,每一个数据块的加密和解密过程都依赖上一个数据块。一旦有一个数据块出现错误将会出现“雪崩效应”。
2.2Feistel网络
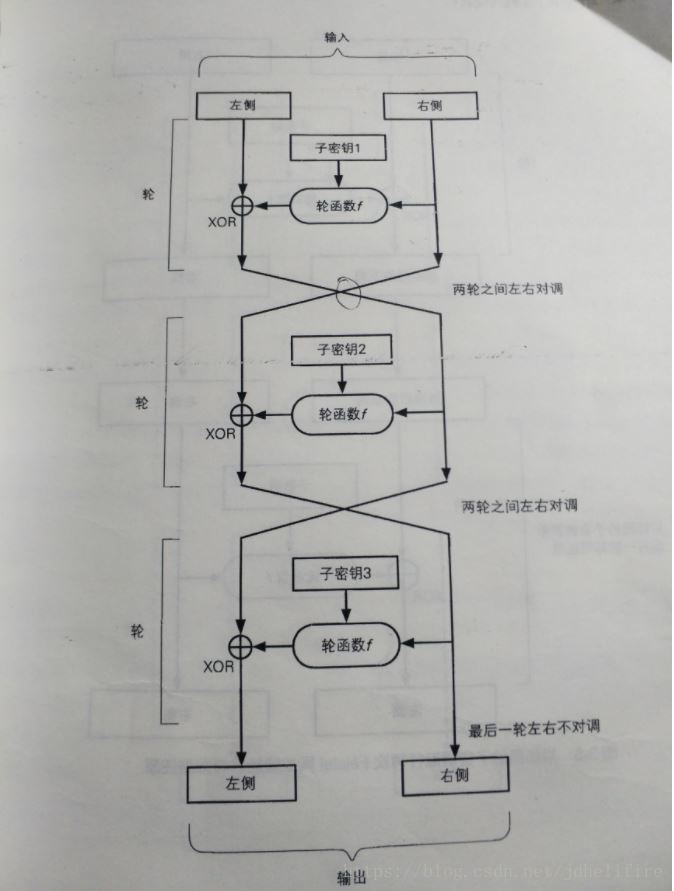
如上图所示Feistel网络实现对于单个数据块的加密。Feistel迭代开始前将64bit数据块拆分为左右32比bit,然后进行如上图所示的迭代过程,总共迭代16次。每一次迭代的子密钥是不同的。每次迭代过程都是对右半部分数据块采用轮函数处理(加密)。所以这里涉及到两个问题:1.子密钥如何产生,2.轮函数如何实现
2.2.1子密钥的生成
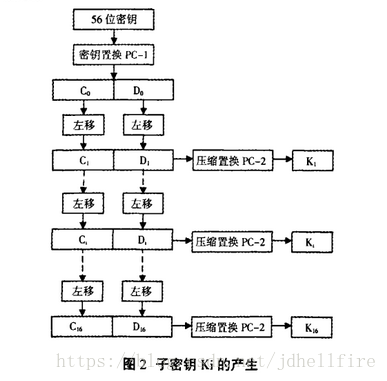
子密钥的生成如上图所示,用户输入的是64bit的密钥(8个字符)首先做一次ip置换将64bit的密钥置换为56bit的密钥。56bit的密钥再进行一次PC-1置换后拆分为左右28bit的密钥。进行16轮迭代,产生16个子密钥。每次迭代将左右28bit密钥做左移1位的运算,然后再进行 PC-2的置换,组合再一起后得到ki。
2.2.1子轮函数的实现
轮函数的实现主要是进行了 ebox的置换处理和sbox的置换处理:
1. ebox 将32bit 的R block 通过扩展置换为48bit的R block,然后与当前迭代的子密钥Ki做XOR 运算,最后拆分为6*8的矩阵。
2. sbox 取 R block每一行的6个bit做运算,得到 sbox的坐标,取到sbox的值后做位移运算得到加密后的新的R block的行,迭代8此后得到最后的加密结果。
总体来说子密钥的生成的实现逻辑和轮函数的实现逻辑较为复杂具体可以参考我的代码实现。
三.代码实现:
Demo版的实现参考了pyDES库,把里面的实现做了一下逻辑抽离等重构操作。只实现了DES-CBC
from re import findall
"""
DES-CBC算法 的DEMO
coding by liuwei 2018.3.23
"""
class DES:
# Permutation and translation tables for DES
__pc1 = [
56, 48, 40, 32, 24, 16, 8,
0, 57, 49, 41, 33, 25, 17,
9, 1, 58, 50, 42, 34, 26,
18, 10, 2, 59, 51, 43, 35,
62, 54, 46, 38, 30, 22, 14,
6, 61, 53, 45, 37, 29, 21,
13, 5, 60, 52, 44, 36, 28,
20, 12, 4, 27, 19, 11, 3
]
# number left rotations of pc1
__left_rotations = [
1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1
]
# permuted choice key (table 2)
__pc2 = [
13, 16, 10, 23, 0, 4,
2, 27, 14, 5, 20, 9,
22, 18, 11, 3, 25, 7,
15, 6, 26, 19, 12, 1,
40, 51, 30, 36, 46, 54,
29, 39, 50, 44, 32, 47,
43, 48, 38, 55, 33, 52,
45, 41, 49, 35, 28, 31
]
# initial permutation IP
__ip = [57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7,
56, 48, 40, 32, 24, 16, 8, 0,
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6
]
# Expansion table for turning 32 bit blocks into 48 bits
__expansion_table = [
31, 0, 1, 2, 3, 4,
3, 4, 5, 6, 7, 8,
7, 8, 9, 10, 11, 12,
11, 12, 13, 14, 15, 16,
15, 16, 17, 18, 19, 20,
19, 20, 21, 22, 23, 24,
23, 24, 25, 26, 27, 28,
27, 28, 29, 30, 31, 0
]
# The (in)famous S-boxes
__sbox = [
# S1
[14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],
# S2
[15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],
# S3
[10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],
# S4
[7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],
# S5
[2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],
# S6
[12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],
# S7
[4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],
# S8
[13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
]
# 32-bit permutation function P used on the output of the S-boxes
__p = [
15, 6, 19, 20, 28, 11,
27, 16, 0, 14, 22, 25,
4, 17, 30, 9, 1, 7,
23, 13, 31, 26, 2, 8,
18, 12, 29, 5, 21, 10,
3, 24
]
# final permutation IP^-1
__fp = [
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25,
32, 0, 40, 8, 48, 16, 56, 24
]
__inter_round = range(16)
def __init__(self, key, iter_mod, IV, pad='\0', ):
# 64bit字符串key,转换为56bit key
self.__key = self.__permutate(self.__pc1, string_to_bit_lst(key))
self.__pad = pad
self.__iter_mod = iter_mod
self.__IV = IV
# 每个block做16轮迭代,为没轮迭代创建SubKey
self.Kn = self.__create_sub_keys()
def __create_sub_keys(self):
"""56bit key 转 16个48bit sub key"""
# 初始化subkey,16轮迭代16个48bit的subkey
Kn = [[0] * 48] * len(self.__inter_round)
# 56bit key分割作为左右两半
L = self.__key[:28]
R = self.__key[28:]
# 循环左移,每次迭代循环左移的次数不一样,由 __left_rotations决定
for round in self.__inter_round:
# 执行循环左移,移动的次数为 __left_rotations[round]
# 循环左移即不断把队列头的元素往对了尾上放
for _ in range(self.__left_rotations[round]):
L.append(L.pop(0))
R.append(R.pop(0))
# 56 Bit key to 48 Bit Subkey
Kn[round] = self.__permutate(self.__pc2, L + R)
return Kn
def encrpyt(self, data):
iv = string_to_bit_lst(self.__IV)
if self.__iter_mod == 'CBC':
return CBC.encrypt_iter(self._encrypt_a_block, self.__data_add_pading(data), iv)
def decrypt(self, data):
iv = string_to_bit_lst(self.__IV)
if self.__iter_mod == 'CBC':
return self.__data_rm_pading(CBC.decrypt_iter(self._decrypt_a_block, data, iv))
def _encrypt_a_block(self, block):
"""加密一个block"""
return self.__crypt_a_block(self.__inter_round, block)
def _decrypt_a_block(self, block):
"""解密一个block即加密一个block的反向过程"""
return self.__crypt_a_block(reversed(self.__inter_round), block)
def __crypt_a_block(self, iter_round, block):
"""
Feistel 网络的迭代过程
"""
# 初始置换
block = self.__permutate(self.__ip, block)
self.L = block[:32]
self.R = block[32:]
# 标准的DES算法迭代16轮
for round in iter_round:
# 右半block 做一个Copy直接作为下次迭代左半block
R_copy = self.R[:]
# Feistel 网络的轮函数处理
self.__round_function(round, self.Kn)
# 轮函数处理过的右半Block与左半Block做xor运算得到下次迭代的右半Block
self.R = self.__xor_left_right_block(self.R, self.L)
self.L = R_copy
return self.__permutate(self.__fp, self.R + self.L)
def __round_function(self, round, Kn):
# eBox置换
R_arry = self.__e_box_handle(round, Kn, self.R)
# sBox置换
self.R = self.__s_box_handle(R_arry)
def __xor_left_right_block(self, R, L):
return list(map(lambda x, y: x ^ y, R, L))
def __e_box_handle(self, round, Kn, R):
# 32bit R Block 扩展为转换为48Bit Block
self.R = self.__permutate(self.__expansion_table, R)
# 取当且迭代的sub key 与48Bit R Block做异或运算
self.R = list(map(lambda x, y: x ^ y, self.R, Kn[round]))
# 将48Bit R block转换为 6*8矩阵
return [self.R[:6], self.R[6:12], self.R[12:18], self.R[18:24], self.R[24:30], self.R[30:36], self.R[36:42],
self.R[42:]]
def __s_box_handle(self, arry):
block = [0] * 32
pos = 0
for j in range(8):
# 取6*8 R block 矩阵的每一行做如下操作 得到sbox 列坐标,
m = (arry[j][0] << 1) + arry[j][5]
n = (arry[j][1] << 3) + (arry[j][2] << 2) + (arry[j][3] << 1) + arry[j][4]
# 得到当前迭代sbox的value
v = self.__sbox[j][(m << 4) + n]
# 通过sbox当前迭代的value得到新的32bit R block
block[pos] = (v & 8) >> 3
block[pos + 1] = (v & 4) >> 2
block[pos + 2] = (v & 2) >> 1
block[pos + 3] = v & 1
pos += 4
# Permutate the concatination of B[1] to B[8] (Bn)
R = self.__permutate(self.__p, block)
return R
def __permutate(self, table, block):
"""Permutate this block with the specified table"""
return list(map(lambda x: block[x], table))
def __data_add_pading(self, data):
# 填满8的整数倍
pad_len = 8 - (len(data) % 8) if (len(data) % 8) != 0 else 0
data += self.__pad * pad_len
return data
def __data_rm_pading(self, data):
return data[:-8].decode() + data[-8:].decode().rstrip(self.__pad)
class CBC:
@staticmethod
def encrypt_iter(block_encrypt_method, data, iv):
result = []
# 加密迭代过程是先xor,后加密
for block in findall(r'.{8}', data):
block = string_to_bit_lst(block)
block = list(map(lambda x, y: x ^ y, block, iv))
encrypted_block = block_encrypt_method(block)
iv = encrypted_block
result.append(bit_lst_to_string(encrypted_block))
return bytes.fromhex('').join(result)
@staticmethod
def decrypt_iter(block_decrypt_method, data, iv):
result = []
# 解密迭代过程是先解密,后xor
for i in range(0, len(data), 8):
block = string_to_bit_lst(data[i:i + 8])
decrypted_block = block_decrypt_method(block)
decrypted_block = list(map(lambda x, y: x ^ y, decrypted_block, iv))
iv = block
result.append(bit_lst_to_string(decrypted_block))
return bytes.fromhex('').join(result)
# 这两个工具函数,直接copy pyDes库的,先不考虑cleanCode
def string_to_bit_lst(data):
"""Turn the string data, into a list of bits (1, 0)'s"""
if isinstance(data, str):
data = [ord(c) for c in data]
l = len(data) * 8
result = [0] * l
pos = 0
for ch in data:
i = 7
while i >= 0:
if ch & (1 << i) != 0:
result[pos] = 1
else:
result[pos] = 0
pos += 1
i -= 1
return result
def bit_lst_to_string(data):
"""Turn the list of bits -> data, into a string"""
result = []
pos = 0
c = 0
while pos < len(data):
c += data[pos] << (7 - (pos % 8))
if (pos % 8) == 7:
result.append(c)
c = 0
pos += 1
return bytes(result)
————————————————
版权声明:本文为CSDN博主「牛屁哄哄叫兽」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/jdhellfire/article/details/79680456
分组加密的四种模式
加密一般分为对称加密(Symmetric Key Encryption)和非对称加密(Asymmetric Key Encryption)。
对称加密又分为分组加密和序列密码。
分组密码,也叫块加密(block cyphers),一次加密明文中的一个块。是将明文按一定的位长分组,明文组经过加密运算得到密文组,密文组经过解密运算(加密运算的逆运算),还原成明文组。
序列密码,也叫流加密(stream cyphers),一次加密明文中的一个位。是指利用少量的密钥(制乱元素)通过某种复杂的运算(密码算法)产生大量的伪随机位流,用于对明文位流的加密。
解密是指用同样的密钥和密码算法及与加密相同的伪随机位流,用以还原明文位流。
在分组加密算法中,有ECB,CBC,CFB,OFB这几种算法模式。
1)ECB(Electronic Code Book)/电码本模式
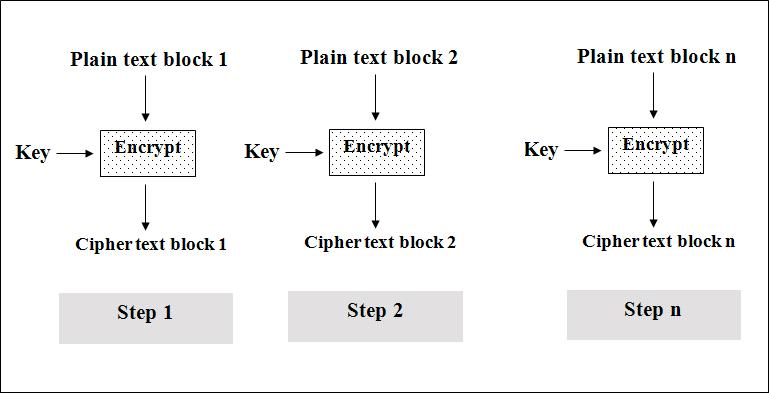
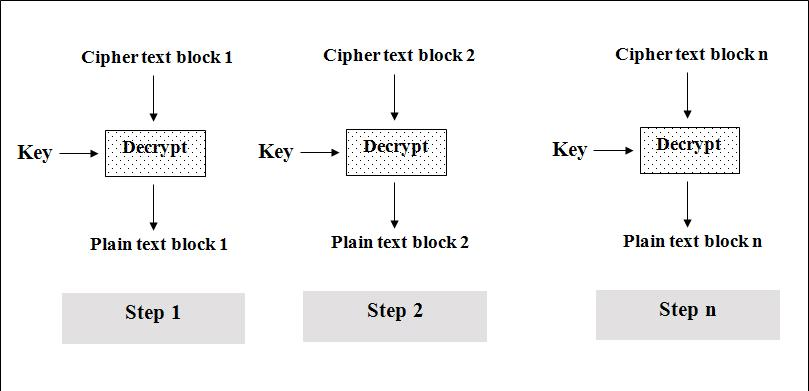
1.简单,有利于并行计算,误差不会被传送;
2.不能隐藏明文的模式;
repetitions in message may show in cipher text/在密文中出现明文消息的重复
3.可能对明文进行主动攻击;
加密消息块相互独立成为被攻击的弱点/weakness due to encrypted message blocks being independent
2)CBC(Cipher Block Chaining)
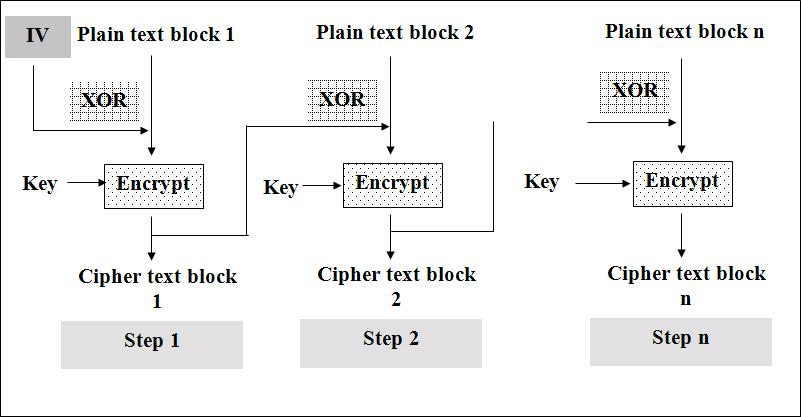
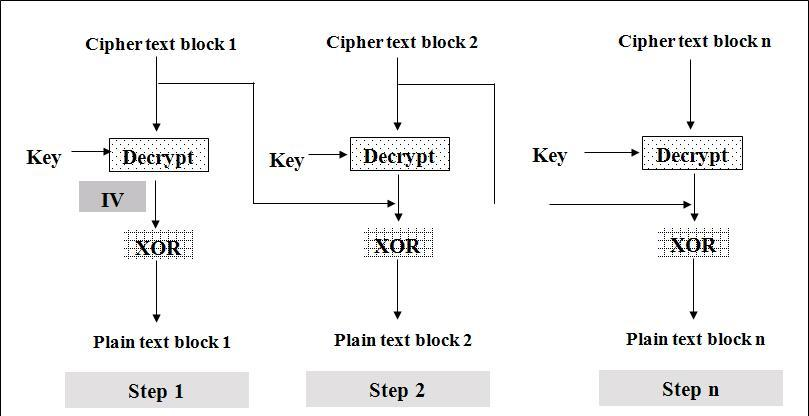
这个词在分组密码中经常会用到,它是指一个明文分组在被加密之前要与前一个的密文分组进行异或运算。当加密算法用于此模式的时候除密钥外,还需协商一个初始化向量(IV),这个IV没有实际意义,只是在第一次计算的时候需要用到而已。采用这种模式的话安全性会有所提高。
1. 不容易主动攻击,安全性好于ECB,适合传输长度长的报文,是SSL、IPSec的标准。
each ciphertext block depends on all message blocks/每个密文块依赖于所有的信息块
thus a change in the message affects all ciphertext blocks/明文消息中一个改变会影响所有密文块
2. need Initial Vector (IV) known to sender & receiver/发送方和接收方都需要知道初始化向量
3.加密过程是串行的,无法被并行化(在解密时,从两个邻接的密文块中即可得到一个平文块。因此,解密过程可以被并行化);误差传递
3)Cipher Feedback (CFB)
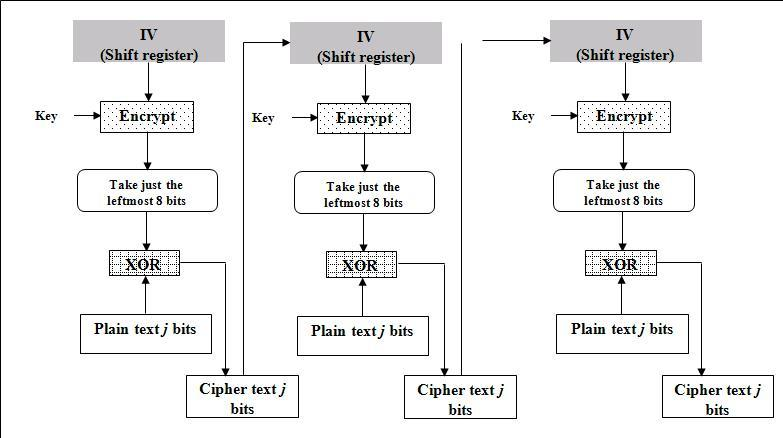
密文反馈(CFB,Cipher feedback)模式类似于CBC,可以将块密码变为自同步的流密码;工作过程亦非常相似,CFB的解密过程几乎就是颠倒的CBC的加密过程:
需要使用一个与块的大小相同的移位寄存器,并用IV将寄存器初始化。然后,将寄存器内容使用块密码加密,然后将结果的最高x位与平文的x进行异或,以产生密文的x位。下一步将生成的x位密文移入寄存器中,并对下面的x位平文重复这一过程。解密过程与加密过程相似,以IV开始,对寄存器加密,将结果的高x与密文异或,产生x位平文,再将密文的下面x位移入寄存器。
与CBC相似,平文的改变会影响接下来所有的密文,因此加密过程不能并行化;而同样的,与CBC类似,解密过程是可以并行化的。
4)Output Feedback (OFB)
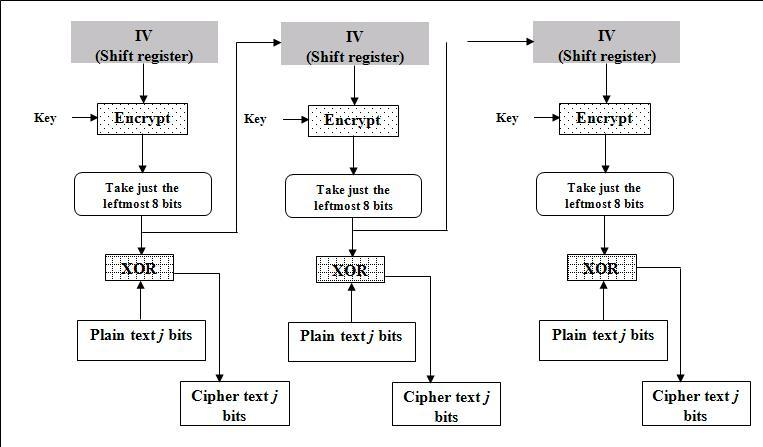
输出反馈模式(Output feedback, OFB)可以将块密码变成同步的流密码。它产生密钥流的块,然后将其与平文块进行异或,得到密文。与其它流密码一样,密文中一个位的翻转会使平文中同样位置的位也产生翻转。这种特性使得许多错误校正码,例如奇偶校验位,即使在加密前计算而在加密后进行校验也可以得出正确结果。
每个使用OFB的输出块与其前面所有的输出块相关,因此不能并行化处理。然而,由于平文和密文只在最终的异或过程中使用,因此可以事先对IV进行加密,最后并行的将平文或密文进行并行的异或处理。
可以利用输入全0的CBC模式产生OFB模式的密钥流。这种方法十分实用,因为可以利用快速的CBC硬件实现来加速OFB模式的加密过程。
————————————————
原文链接:https://blog.csdn.net/fw0124/article/details/8472560



