二维数组中的查找——剑指Offer
题目描述
在一个二维数组中(每个一维数组的长度相同),
每一行都按照从左到右递增的顺序排序,
每一列都按照从上到下递增的顺序排序。
请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
解题思路
要求时间复杂度 O(M + N),空间复杂度 O(1)。其中 M 为行数,N 为 列数。
该二维数组中的一个数,小于它的数一定在其左边,大于它的数一定在其下边。
因此,从右上角开始查找,就可以根据 target 和当前元素的大小关系来缩小查找区间,当前元素的查找区间为左下角的所有元素。
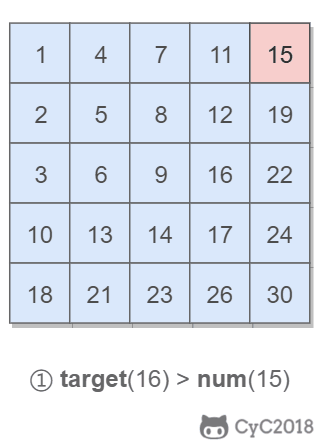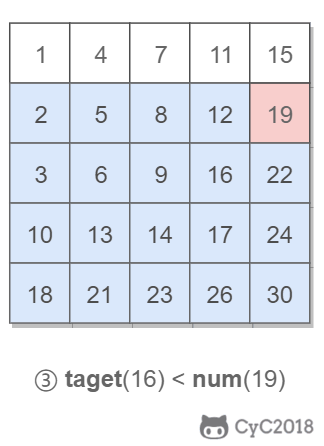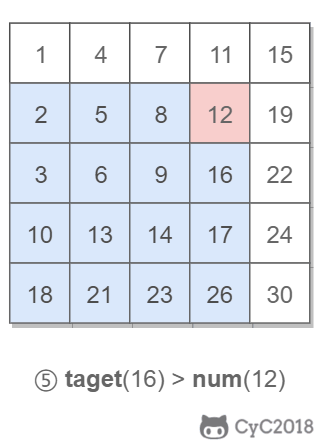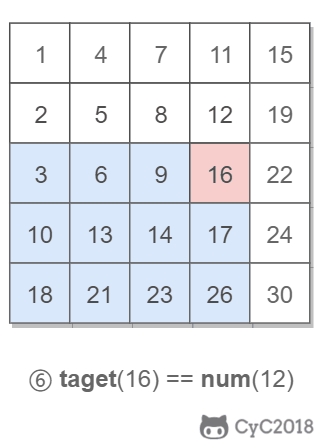
public boolean Find(int target, int [][] array) {
//首先进行判空 if(array==null||array.length==0||array[0].length==0) { return false; }
//获得行数与列数 int rows=array.length,cols=array[0].length;
//定义下标变量 int r=0,c=cols-1;
//从右上角到左下角依次寻找 while(r <= rows-1 && c >= 0){
//找到目标数字 if(target==array[r][c]){ return true; }
//目标数字小于当前数字 if(target<array[r][c]){ c--; }else{//目标数字大于当前数字 r++; } }
//直到找完整个二维数组,都没有找到目标数字。 return false; }


