【学习笔记】线段树二分
这是真正的线段树二分
首先拆分询问区间。可以证明每一层遍历到的区间不会超过
4
4
4 个。所以复杂度是
log
n
\log n
logn 。
类似的,可以通过 递归左子树->等待答案->递归右子树 的方法来查询 [l,r] 中最右或最左的满足条件的点。复杂度同样是
log
n
\log n
logn 。
例题1:CF689D Friends and Subsequences
求满足下列条件的区间
[
l
,
r
]
[l,r]
[l,r] 的数量,
n
≤
2
e
5
n\leq 2e5
n≤2e5 。

solution:
固定 l 端点,二分 r 端点,设函数 qry1(p,L,R) 表示 [L,R] 中满足 max(a_l,a_{l+1},…,a_k)>min(b_l,b_{l+1},…,b_k) 的最小的点,其中 L<=k<=R 。
同理设 qry2(p,L,R) 表示 [L,R] 中满足 max(a_l,a_{l+1},…,a_k)<min(b_l,b_{l+1},…,b_k) 的最大的点,其中 L<=k<=R 。
那么用全局变量 MIN,MAX 记录遍历到的所有点中的最大值,最小值,每次递归左子树,等待答案,再递归右子树,时间复杂度 O(nlogn) 。
关于 qry1 :
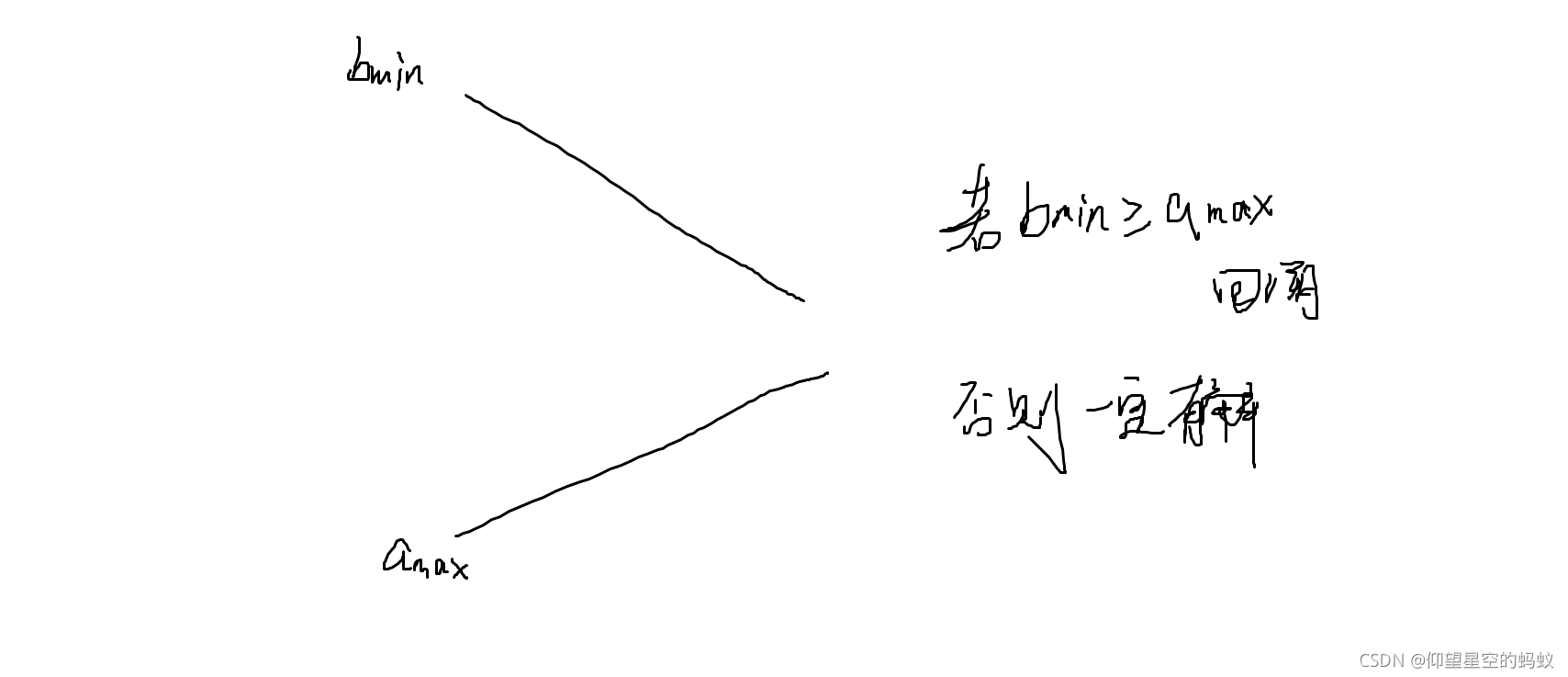
关于 qry2:
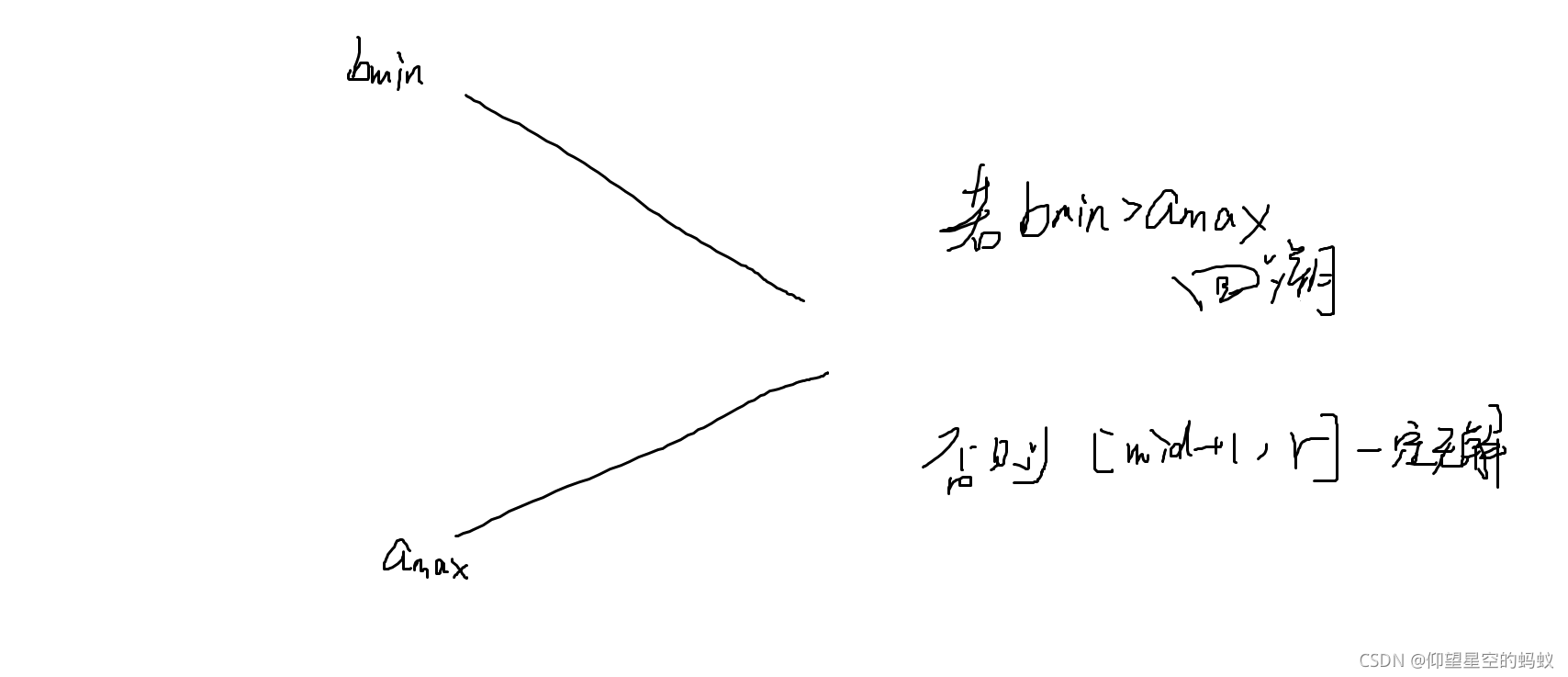
上述两图证明了任意时刻都只会遍历左右子树中的一个(分叉点除外),复杂度得到证明。
总结:本题线段树二分做法依赖于单调性,做题时要善于观察。
#include<bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
const int Maxn=2e5+5;
int n,a[Maxn],b[Maxn],MAX,MIN;
ll res;
struct SegmentTree{
int Max[Maxn<<2],Min[Maxn<<2];
void build(int p,int l,int r) {
if(l==r) {
Max[p]=a[l];
Min[p]=b[l];
return;
}
int mid=l+r>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
Max[p]=max(Max[p<<1],Max[p<<1|1]);
Min[p]=min(Min[p<<1],Min[p<<1|1]);
}
int qry1(int p,int l,int r,int ql,int qr) {
int mid=l+r>>1;
if(ql<=l&&r<=qr) {
int tmax=max(MAX,Max[p]);
int tmin=min(MIN,Min[p]);
if(tmax<=tmin) {
MAX=tmax;
MIN=tmin;
return r+1;
}
if(l==r) return l;
int now=qry1(p<<1,l,mid,ql,qr);
if(now==mid+1) now=qry1(p<<1|1,mid+1,r,ql,qr);
return now;
}
else if(ql<=mid&&mid<qr) {
int now=qry1(p<<1,l,mid,ql,qr);
if(now==mid+1) now=qry1(p<<1|1,mid+1,r,ql,qr);
return now;
}
else if(qr<=mid) return qry1(p<<1,l,mid,ql,qr);
else return qry1(p<<1|1,mid+1,r,ql,qr);
}
int qry2(int p,int l,int r,int ql,int qr) {
int mid=l+r>>1;
if(ql<=l&&r<=qr) {
int tmax=max(MAX,Max[p]);
int tmin=min(MIN,Min[p]);
if(tmax<tmin) {
MAX=tmax;
MIN=tmin;
return r;
}
if(l==r) return l-1;
int now=qry2(p<<1,l,mid,ql,qr);
if(now==mid) now=qry2(p<<1|1,mid+1,r,ql,qr);
return now;
}
else if(ql<=mid&&mid<qr) {
int now=qry2(p<<1,l,mid,ql,qr);
if(now==mid) now=qry2(p<<1|1,mid+1,r,ql,qr);
return now;
}
else if(qr<=mid) return qry2(p<<1,l,mid,ql,qr);
else return qry2(p<<1|1,mid+1,r,ql,qr);
}
}T1;
int main() {
// freopen("data.in","r",stdin);
scanf("%d",&n);
for(int i=1;i<=n;i++) {
scanf("%d",&a[i]);
}
for(int i=1;i<=n;i++) {
scanf("%d",&b[i]);
}
T1.build(1,1,n);
for(int i=1;i<=n;i++) {
MAX=-INF,MIN=INF;
int pr=T1.qry1(1,1,n,i,n);
MAX=-INF,MIN=INF;
int pl=T1.qry2(1,1,n,i,n);
res+=pr-pl-1;
}
printf("%lld",res);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号