题解

网络流经典问题，希望大家不要死记模型，要会自己建模

本文会详细讲解网络流的基础建模方法

 

先来看一下闭合图是什么

放一张论文的图片：

意思就是说，某些决策具有依赖性，这些依赖关系构成了一个DAG（如果是树就可以树形DP）

就可以使用最大权闭合图模型

最大权闭合图模型的原理是什么呢？

 

让我们先回到最小割的定义：把S集合与T集合割开的最小代价

如图：（割的方式一共有四种，红色的割线是最小割）

假设现在点与点之间没有任何关联

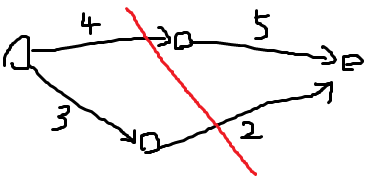
我们会发现，每一种割的方式都会对应一个选点的集合

而对于一个点u，我们如果想把它选入S集合，我们就得割掉u—>T的边，并付出代价

如果不把它分入S集合，我们就要割掉S—>u的边，并付出代价

如果我们想找到最小的代价来选出S集合，那么最小割一定对应了最小的代价

这才是最基本的模型

 

再回到最大权闭合图

这个选集合的过程中，如果某些点之间有依赖关系（比如说选A必选B），我们就可以加一条从A向B容量为INF的边

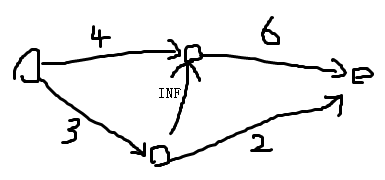
此时我们发现依然有四种割集，但是其中一种割集中含有边INF，所以这种割集会在计算答案时被排除。

而被排除的这种割集恰好对应了不满足依赖关系的选点方案

（关于这种构造方式的可行性、最优性证明在胡伯涛论文中有）

 

所以我们就有了一个解决最大权闭合图的朴素方法

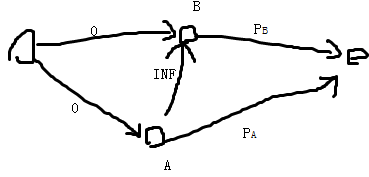
由于P可能为负，所以就需要把所有的边容量加一个值，保证所有的边容量均为正数，最后算答案的时候减掉

 

对于这道题而言，把边也看成点，边权可以带来利润，就可以减少选出S集合的代价。

用这种建图方式就可以过了（虽然复杂度明显不对）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 100015
#define M 600005
const int INF=0x3f3f3f3f;
int fir[N],to[M],nxt[M],cap[M],cnt;
void adde(int a,int b,int c1,int c2)
{
	to[++cnt]=b;nxt[cnt]=fir[a];fir[a]=cnt;cap[cnt]=c1;
	to[++cnt]=a;nxt[cnt]=fir[b];fir[b]=cnt;cap[cnt]=c2;
}
int S,T,d[N],vd[N],flow;
int sap(int u,int aug)
{
	if(u==T) return aug;
	int tmp,ret=0,mind=T-1;
	for(int v,p=fir[u];p;p=nxt[p]){
		v=to[p];
		if(cap[p]>0){
			if(d[u]==d[v]+1){
				tmp=sap(v,min(cap[p],aug));
				cap[p]-=tmp;aug-=tmp;
				cap[p^1]+=tmp;ret+=tmp;
				if(aug==0||d[S]>=T) return ret;
			}
			mind=min(mind,d[v]);
		}
	}
	if(ret==0){
		vd[d[u]]--;
		if(vd[d[u]]==0)
			d[S]=T;
		d[u]=mind+1;
		vd[d[u]]++;
	}
	return ret;
}
void f()
{
	memset(d,0,sizeof(d));
	memset(vd,0,sizeof(vd));
	vd[0]=T;flow=0;
	while(d[S]<T)
		flow+=sap(S,INF);
}
#define mov 101
int main()
{
	cnt=1;
	int n,m,i,u,v,x;
	scanf("%d%d",&n,&m);
	S=m+n+1;T=m+n+2;
	for(i=1;i<=n;i++){
		scanf("%d",&x);
		adde(S,i+m,mov,0);
		adde(i+m,T,x+mov,0);
	}
	for(i=1;i<=m;i++){
		scanf("%d%d%d",&u,&v,&x);
		adde(i,u+m,INF,0);
		adde(i,v+m,INF,0);
		adde(S,i,mov,0);
		adde(i,T,-x+mov,0);
	}
	f();
	printf("%d",mov*(n+m)-flow);
}

 

 

如果想要在保持连通性的情况下建立模型

我们可以把S连边指向有利润的点，容量为利润，需要代价的点向T连边，容量为代价

这样的模型会更加优美简单

如论文的建模：

虽然时间复杂度还是明显不对，但有所优化。（(n+m)^2*(n+m)）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 100015
#define M 400005
const int INF=0x3f3f3f3f;
int fir[N],to[M],nxt[M],cap[M],cnt;
void adde(int a,int b,int c1,int c2)
{
	to[++cnt]=b;nxt[cnt]=fir[a];fir[a]=cnt;cap[cnt]=c1;
	to[++cnt]=a;nxt[cnt]=fir[b];fir[b]=cnt;cap[cnt]=c2;
}
int S,T,d[N],vd[N],flow;
int sap(int u,int aug)
{
	if(u==T) return aug;
	int tmp,ret=0,mind=T-1;
	for(int v,p=fir[u];p;p=nxt[p]){
		v=to[p];
		if(cap[p]>0){
			if(d[u]==d[v]+1){
				tmp=sap(v,min(cap[p],aug));
				cap[p]-=tmp;aug-=tmp;
				cap[p^1]+=tmp;ret+=tmp;
				if(aug==0||d[S]>=T) return ret;
			}
			mind=min(mind,d[v]);
		}
	}
	if(ret==0){
		vd[d[u]]--;
		if(vd[d[u]]==0)
			d[S]=T;
		d[u]=mind+1;
		vd[d[u]]++;
	}
	return ret;
}
void f()
{
	memset(d,0,sizeof(d));
	memset(vd,0,sizeof(vd));
	vd[0]=T;flow=0;
	while(d[S]<T)
		flow+=sap(S,INF);
}
int main()
{
	cnt=1;
	int n,m,i,u,v,x,sum=0;
	scanf("%d%d",&n,&m);
	S=m+n+1;T=m+n+2;
	for(i=1;i<=n;i++){
		scanf("%d",&x);
		adde(i+m,T,x,0);
	}
	for(i=1;i<=m;i++){
		scanf("%d%d%d",&u,&v,&x);
		adde(i,u+m,INF,0);
		adde(i,v+m,INF,0);
		adde(S,i,x,0);
		sum+=x;
	}
	f();
	printf("%d",sum-flow);
}

 

 

 

 

下面介绍一个更优的建模方法（不用边转点）

由于每条边只有两个端点是它的传递闭包

所以我们的答案就可以化为

选出一个子图G‘={V'，E'}

最大化：（其中pv规定为负数）

\sum_{e\in E'}w_e+\sum_{v\in V'}p_v

接下来就是一个技巧，把边权转到对点权的求和上

\sum_{e\in E'}w_e=\frac{\sum_{v\in V'}{d_v}-mincut[V',V-V']}{2}

（其中dv为与点v相邻的边的权值和）

为什么呢？

我们把V'集合中的点的相邻边的权值和加起来，会发现集合内部的边会算两次，红色的边会算一次

而红色边的边权就是V'与V'的补集的割的大小（由于我们想要最大化该式子的值，所以取最小割）

 

继续化式子：

\frac{\sum_{v\in V'}d_v-mincut[V',V-V']}{2}+\sum_{v\in V'}p_v

乘以2不影响式子（最后再除掉2）

\sum_{v\in V'}d_v-mincut[V',V-V']+2*\sum_{v\in V'}p_v

\sum_{v\in V'}{(d_v+2*p_v)}-mincut[V',V-V']

乘个-1，变成最小化：

mincut[V',V-V']-\sum_{v\in V'}{(d_v+2*p_v)}

我们想把后面那一坨式子放到求最小割的时候去做

就可以利用我们之前的选点模型，把每个点都连边向T，容量为-dv-2*pv

再把S到v和v到T的边的容量加一个较大值，保证边权非负，最后再减掉

虽然时间复杂度还是不对，但是这已经是本题的时间复杂度下限。（n^2*(n+m)）

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 5015
#define M 200005
const int INF=0x3f3f3f3f;
int fir[N],to[M],nxt[M],cap[M],cnt;
void adde(int a,int b,int c1,int c2)
{
	to[++cnt]=b;nxt[cnt]=fir[a];fir[a]=cnt;cap[cnt]=c1;
	to[++cnt]=a;nxt[cnt]=fir[b];fir[b]=cnt;cap[cnt]=c2;
}
int S,T,d[N],vd[N],flow;
int sap(int u,int aug)
{
	if(u==T) return aug;
	int tmp,ret=0,mind=T-1;
	for(int v,p=fir[u];p;p=nxt[p]){
		v=to[p];
		if(cap[p]>0){
			if(d[u]==d[v]+1){
				tmp=sap(v,min(cap[p],aug));
				cap[p]-=tmp;aug-=tmp;
				cap[p^1]+=tmp;ret+=tmp;
				if(aug==0||d[S]>=T) return ret;
			}
			mind=min(mind,d[v]);
		}
	}
	if(ret==0){
		vd[d[u]]--;
		if(vd[d[u]]==0)
			d[S]=T;
		d[u]=mind+1;
		vd[d[u]]++;
	}
	return ret;
}
void f()
{
	memset(d,0,sizeof(d));
	memset(vd,0,sizeof(vd));
	vd[0]=T;flow=0;
	while(d[S]<T)
		flow+=sap(S,INF);
}
int p[N],du[N];
struct node{int u,v,c;}e[M];
int main()
{
	cnt=1;
	int n,m,i,U=0;
	scanf("%d%d",&n,&m);
	S=n+1;T=n+2;
	for(i=1;i<=n;i++){
		scanf("%d",&p[i]);
		U+=2*p[i];
	}
	for(i=1;i<=m;i++){
		scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].c);
		U+=e[i].c;
		du[e[i].u]+=e[i].c;du[e[i].v]+=e[i].c;
		adde(e[i].u,e[i].v,e[i].c,e[i].c);
	}
	for(i=1;i<=n;i++){
		adde(S,i,U,0);
		adde(i,T,U+2*p[i]-du[i],0);
	}
	f();
	printf("%d",(U*n-flow)/2);
}

 

这种方法在胡伯涛论文中有所提及