题面:#6073. 「2017 山东一轮集训 Day5」距离
题解
好题
又是原题重测的题
大概就是让我们求
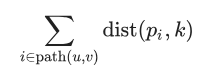
感觉一点思路都没有啊。。。
那我们先来看一个超级弱化版的题目([LNOI2014]LCA)
它是让我们求
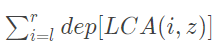
这个题目相比之下就简单了许多
关于计算dep[LCA(i,z)]
我们可以先把i到1的路径上的所有点权都加一,再来求z到1路径的点权和
由于这道题可以利用前缀和来求答案
所以我们只需要离线之后把一个询问拆成两个
依次把1~i加入到树中(加一个点x,就利用树链剖分+线段树把x到1的路径所有点+1)
然后查询z到1路径的点权和即可
再来考虑这道题
似乎还是有点难啊
再来一个3级弱化版的题目
给出l,r,x,求l到r路径上每个点到x的距离之和,所有边权为1,可以离线
这个问题其实有很简单的数学做法,但是由于与此题思路无关,在这里不展开
我们稍加思索,就可以发现
显然dis(1,i)和dis(1,x)是非常好做的,也支持点到根路径的快速求和(预处理即可)
而dis(1,lca)就可以利用与上一道题的类似的方法
如果可以离线的话,我们就dfs整棵树,每新遇到一个点就把它到根节点的路径的所有点+1(出栈的时候就-1)
每一个询问都可以拆分成4个来做
dfs到一个点,就先把当前点加入树链剖分的线段树里面O(log^2n),再对这个点上的询问进行求值,均摊O(log^2n)
然后就可以O(nlog^2n)过掉此题
再来一个二级弱化版的题目
给出l,r,x,求l到r路径上每个点到x的距离之和,所有边权为1,强制在线
我们发现,上一道题之所以可以到一个点求出其有关询问的值,是因为我们把这个状态下线段树维护好了
我们又发现,一个点父亲状态的线段树与儿子状态的线段树,只相差了一个链剖区间+1(即把logn个区间+1)的操作
所以我们想到了可持久化线段树,每次都以当前点的父亲线段树为前置版本来进行修改
这样就可以在O(nlog^2n)的空间复杂度里保存每个点对应的线段树
直接在线查询即可
注意可持久化线段树不能写懒标记下传(因为可能下传到过去版本的线段树里)(除非你下传的时候也新建节点)
只能标记永久化
再来一个一级弱化版的题目
给出l,r,x,求l到r路径上每个点到x的距离之和,边权任意,强制在线
我们这次只需要在线段树上动手脚了
由于每个点所增加的权值是固定不变的(这个权值就是它到它父亲的距离)
我们只需要预处理一个dfs序的前缀和,在插入区间的时候把线段树当前节点的值加上ql到qr的前缀和即可
最后我们回到原题
给出l,r,x,求l到r路径上每个点的映射点到x的距离之和,边权任意,强制在线
其实我们最后发现这个映射根本不是难点
只需要在建可持久化线段树的时候把点x代为p[x],照样利用链剖来爬链修改线段树就可以了
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 200005
#define LL long long
int n,Q;
int fir[N],to[2*N],nxt[2*N],cd[2*N],cnt;
void adde(int a,int b,int c)
{
to[++cnt]=b;nxt[cnt]=fir[a];fir[a]=cnt;cd[cnt]=c;
to[++cnt]=a;nxt[cnt]=fir[b];fir[b]=cnt;cd[cnt]=c;
}
int fa[N],son[N],dep[N],siz[N],top[N];
int val[N];LL sum[N],dis[N],dsum[N];
void dfs1(int u)
{
dep[u]=dep[fa[u]]+1;
siz[u]=1;
for(int v,p=fir[u];p;p=nxt[p]){
v=to[p];
if(v!=fa[u]){
fa[v]=u;
val[v]=cd[p];
dis[v]=dis[u]+1ll*cd[p];
dfs1(v);
siz[u]+=siz[v];
if(siz[son[u]]<siz[v])
son[u]=v;
}
}
}
int dfn[N],dc;
void dfs2(int u)
{
dfn[u]=++dc;
if(son[u])top[son[u]]=top[u],dfs2(son[u]);
for(int v,p=fir[u];p;p=nxt[p]){
v=to[p];
if(v!=fa[u]&&v!=son[u])
top[v]=v,dfs2(v);
}
}
int LCA(int x,int y)
{
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
struct node{
int l,r,la;
LL x;
}a[N<<7];
int T[N],P[N],tot;
void insert(int &i,int l,int r,int ql,int qr)
{
a[++tot]=a[i];i=tot;
if(ql==l&&qr==r){a[i].la++;return;}
a[i].x+=sum[qr]-sum[ql-1];
int mid=(l+r)>>1;
if(qr<=mid)insert(a[i].l,l,mid,ql,qr);
else if(ql>mid)insert(a[i].r,mid+1,r,ql,qr);
else insert(a[i].l,l,mid,ql,mid),insert(a[i].r,mid+1,r,mid+1,qr);
}
LL query(int i,int l,int r,int ql,int qr)
{
LL ret=(sum[qr]-sum[ql-1])*a[i].la;
if(ql==l&&qr==r)return ret+a[i].x;
int mid=(l+r)>>1;
if(qr<=mid)return ret+query(a[i].l,l,mid,ql,qr);
else if(ql>mid)return ret+query(a[i].r,mid+1,r,ql,qr);
else return ret+query(a[i].l,l,mid,ql,mid)+query(a[i].r,mid+1,r,mid+1,qr);
}
void dfs(int u)
{
T[u]=T[fa[u]];int x=P[u];
dsum[u]=dsum[fa[u]]+dis[x];
while(top[x]){
insert(T[u],1,n,dfn[top[x]],dfn[x]);
x=fa[top[x]];
}
for(int v,p=fir[u];p;p=nxt[p])
if((v=to[p])!=fa[u]) dfs(v);
}
LL QP(int x,int k)
{
LL ret=dis[k]*dep[x]+dsum[x];
while(top[k]){
ret-=2ll*query(T[x],1,n,dfn[top[k]],dfn[k]);
k=fa[top[k]];
}
return ret;
}
int main()
{
int tp,i;LL u,v,k,ans=0;
scanf("%d%d%d",&tp,&n,&Q);
for(i=1;i<n;i++){
scanf("%lld%lld%lld",&u,&v,&k);
adde(u,v,k);
}
for(i=1;i<=n;i++)scanf("%d",&P[i]);
dfs1(1);top[1]=1;dfs2(1);
for(i=1;i<=n;i++)sum[dfn[i]]=val[i];
for(i=1;i<=n;i++)sum[i]+=sum[i-1];
dfs(1);
while(Q--){
scanf("%lld%lld%lld",&u,&v,&k);
if(tp)u^=ans,v^=ans,k^=ans;
int lca=LCA(u,v);
ans=QP(u,k)+QP(v,k)-QP(lca,k)-QP(fa[lca],k);
printf("%lld\n",ans);
}
}

