OpenGL.tutorial06键盘和鼠标

1、这个图是用 Excel画的 简单示意图（单元格边框，视图-->网格线）

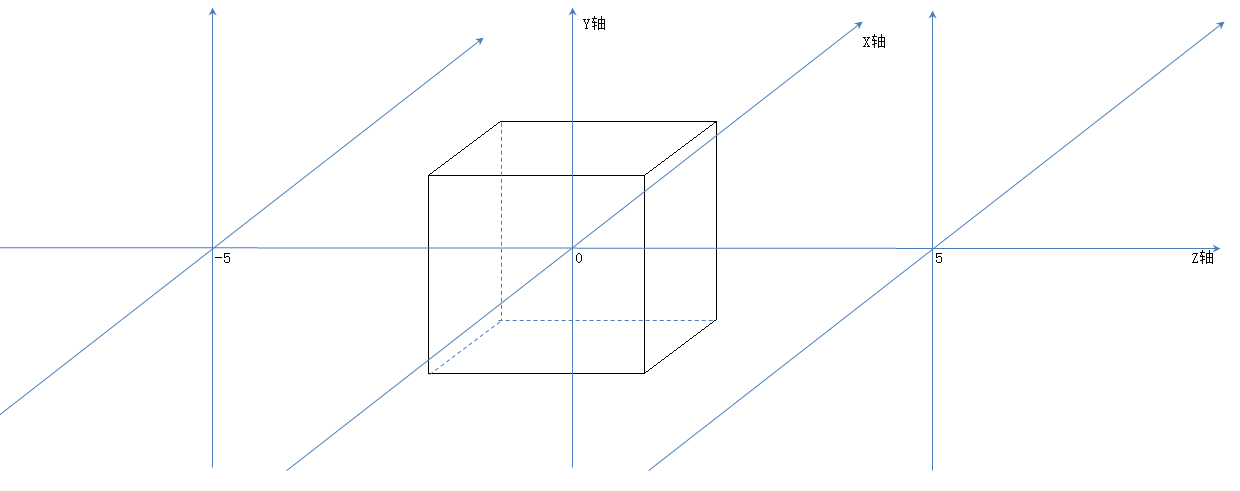
　1.1、中间的 正立方体 处于 X/Y/Z轴的中心，边长为2

　　ZC：代码中 原版是 人物在 (0,0,5)处，水平夹角180°（即 horizontalAngle为180°[弧度为π]），相当于 人物向后转了（应该是 绕向量(0,1,0)逆时针旋转的）

　1.2、代码为：E:\OpenGL_something\ogl-master\common\controls.cpp 中的 "void computeMatricesFromInputs()"

    // Direction : Spherical(球坐标系) coordinates(协调) to Cartesian(笛卡尔的) coordinates conversion(转换)
    glm::vec3 direction(
        cos(verticalAngle) * sin(horizontalAngle), 
        sin(verticalAngle),
        cos(verticalAngle) * cos(horizontalAngle)
        );

 

　　（1）我的操作现象：我将Camera移动到(0,0,-5)的位置，horizontalAngle的初始值 设为0f，这样便于理解

　　　　鼠标往右移--> horizontalAngle为 负值 且 越来越小（绝对值在变大）

　　　　鼠标往上移--> verticalAngle为 正值 且 越来越大

　　（2）效果类似于，CS等的第一人称射击游戏的效果，物体是一直不动的，小键盘↑-->人物往前走-->物体视觉效果上变大，小键盘↓-->人物往后退-->物体视觉效果上变小，小键盘← --> 人物往左移动，小键盘→ --> 人物往右移动，鼠标往哪边动 就是 人物的头往哪边看（光操作鼠标时 人物位置是不动的）

　　（3）我的理解：Camera的位置就是坐在电脑前的人的位置，对应变量 position；变量 direction：可以理解成 人物面向的方向，是由 鼠标的移动操作控制的

　　（4）我的测试：

　　　（A）将 “glm::vec3 position = glm::vec3( 0, 0, 5 ); ”改为“glm::vec3 position = glm::vec3( 0, 0, -5 ); ”　　　

　　　（B）将“float horizontalAngle = 3.14f;”改为“float horizontalAngle = 0;//3.14f;”。　　这样就是 人物从(0, 0, -5)往Z轴正方向看了，不需要转180°(弧度为π)，这样稍微便于理解一点

　　　（C）此时，鼠标往左移 --> horizontalAngle为正值，随着鼠标逐渐往左 horizontalAngle的值逐渐变大；

　　　　　　　　　鼠标往上移 --> verticalAngle为正值，随着鼠标逐渐往上 verticalAngle的值逐渐变大。

　　　（D）下面的图，就是从(0, 0, -5)处往Z轴正方向看，然后 鼠标往左上移动：（E:\Project_VS10\OpenGL_ConsoleTest_zz\tutorial06.xlsx）

　　　　

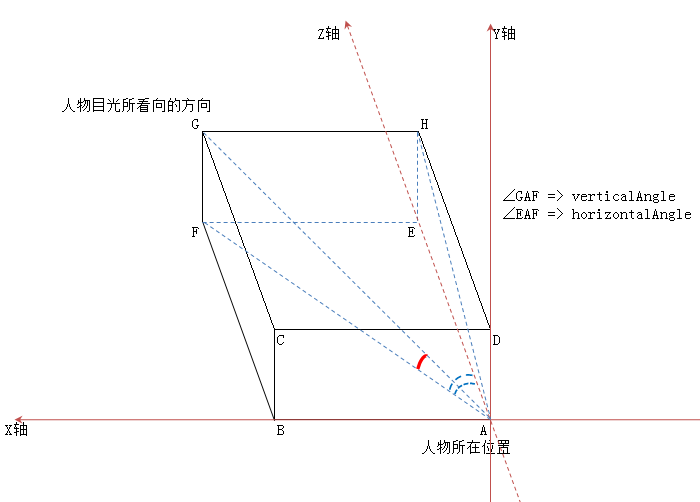
　　　　A就是 在(0, 0, -5)处的人物，目光方向是Z轴正方向，然后 操作鼠标 使人物面向左上方，看向 点G的方向。此时 以点A为中心，线段AG为半径（长度为1），形成一个球体。这里 我们只关心 X&Y&Z轴 正方向的空间区域。

　　　　我根据 代码中，direction的生成公式，反向推断出 horizontalAngle是∠EAF，verticalAngle是∠FAG（∵这样子的 情况 代入代码中的公式正好）。

　　　　我的疑问：我总感觉 horizontalAngle应该是∠HAG，这样理解才对，现在想想 用线段AB的长度来 近似为∠HAG或∠EAF的弧度值 可能差不多？？ 查了一下 球坐标系转笛卡尔坐标系 也没怎么看懂...数学不好要人命啊...

　　　　我的验证过程：(cos(verticalAngle) * sin(horizontalAngle))的平方 + sin(verticalAngle)的平方 + (cos(verticalAngle) * cos(horizontalAngle))的平方 是否等于 1*1。我代入了几个值 发现等式是成立的。

　　　　总结：以现在的水平，搞不懂为什么，记住结论吧先

 

 

 

2、WebGL编程指南.pdf　　　　Pdf.P66

3、

4、

5、