最基础的树：二叉树

树 二叉树 概念

树，是一种非线性数据结构，树中的元素具有明显的层次特性。

在这种数据结构中，每个结点只有一个前驱，却可以有多个后继，类似树，只有一根主干，却可以有很多分支。通常我们研究的是二叉树，即每个结点只能分一叉的树。

二叉树我们可以表示成下图的样子，实际像一棵倒过来的树，或者像一个树根。其有Root根节点，相连的结点构成父子关系，同一个父亲的还构成兄弟关系。

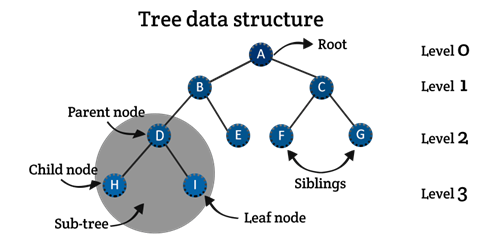
一棵树通常按如下规则编号每个结点，根节点为1号，层数依次向下，每层从左到右，顺序编号。

为了完整的描述一棵树，除了父子结点，我们还需要知道以下几个概念：

• 度：结点的度：该结点拥有的子节点个数；树的度：树中最大的结点的度数；
• 叶子节点：没有儿子的结点称为叶子结点，即度为0的结点，很形象；
• 结点的层次：根节点的层次为1（还要一种说法为0，如上图即为0，本文按为1讨论），其他结点的层次为其父节点层次加1；
• 树的深度：树的深度=所有结点中最大的层次
• 树的高度：就是树有几层，如图有四层，即为4（有的书高度就是深度，有的单独做一个概念）；
• 满二叉树：若树高度为h，结点为2^h-1的树，又称完美二叉树；
• 完全二叉树：深度为k，有n个结点的二叉树当且仅当其每一个结点都与深度为k，有n个结点的满二叉树中编号从1到n的结点一一对应时，称为完全二叉树

树有多叉树和二叉树，使用得较多得是二叉树。二叉树是特殊的树，有下面一些特性：

• 二叉树的第i层最多有2^i-1(i>0)个结点；
• 深度为h的二叉树中至多含有2^h-1个节点；
• 若在任意一棵二叉树中，有n₀个叶子节点，有n₂个度为2的节点，则必有n₀=n₂+1；
• 具有n个结点的完全二叉树深度为log₂n+1；
• 对有n个结点的完全二叉树进行编号：1）第k(k>1)个结点的父节点为k/2向下取整；2）若2k<=n，则k结点的左子节点编号为2k，否则没有子节点；3）若2k+1<=n，则右子节点为2k+1，否则没有右子节点。

二叉树的实现

二叉树可以通过数组实现，也可以通过链表实现。

数组实现

想要使用数组实现二叉树，需要树是完全二叉树，如果不是完全二叉树，我们可以通过补全结点使其成为完全二叉树。

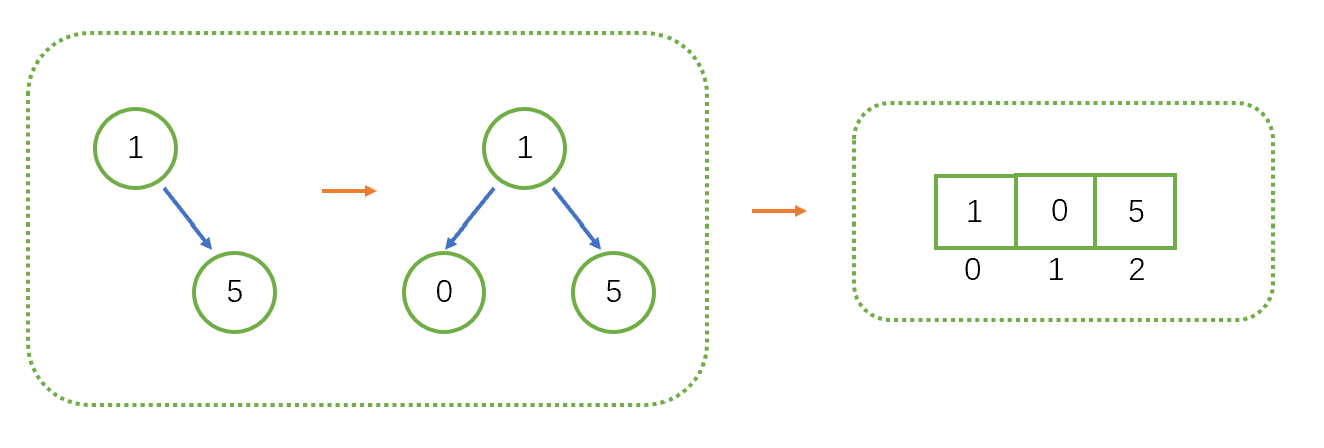
当树成为完全二叉树后，将其按结点顺序存入数组中，根据完全二叉树父子结点编号之间的数学关系，我们可以轻松的找到每一个结点。

这种存储方式简单，但是当树很不满时会造成许多空间浪费。

链表实现

采用链式实现，由上面的图可以看出，当树是二叉树时，链式实现很简单，每个结点包含指向左右儿子的指针和自身数据即可，但当树空缺位置很多，很不满时，就会造成很多的指针的浪费。尤其当树的分叉数不确定时，链式储存会浪费大量空间；不过我们可以采用兄弟结点的方法解决内存浪费，即每个结点都有子指针和兄弟指针。

左右儿子存储：

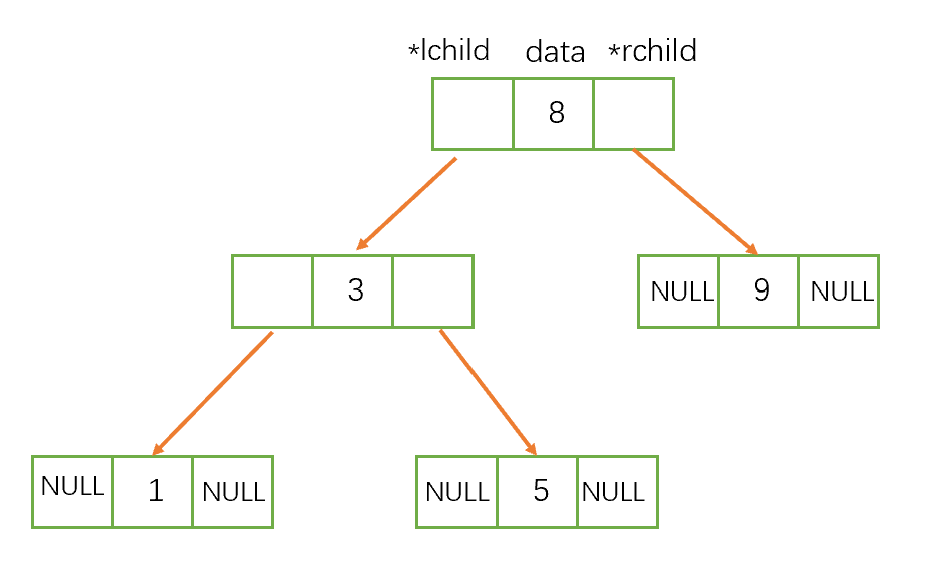
树的结构
typedef struct node{
    int data;
    struct node *left;
    struct node *right;
}*treenode;

树的遍历

遍历一颗二叉树时，每个结点都会访问三次，根据输出结点的时机不同，可以分为三种遍历。

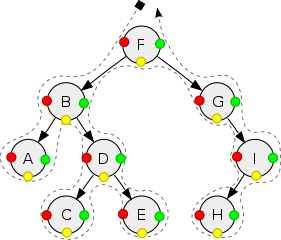
前序遍历

第一次访问该节点时就输出该节点，输出的递归是：根节点-->左子树-->右子树。

中序遍历

第二次访问该节点时输出该节点，输出的递归是：左子树-->根节点-->右子树。

后序遍历

最后一次访问该节点时输出该节点，输出的递归是：左子树-->右子树-->根节点。

递归实现

树采用递归遍历非常简单，我们先看看前序遍历的递归代码：

void preOrder(treenode root){
  if(!root)  return;
  printf("%d ",root->val);  /*①*/
  preOrder(root->left);     /*②*/
  preOrder(root->right);     /*③*/
}

如果先输出根节点再遍历左子树，再遍历右子树就是先序遍历。那么很容易理解中序遍历就是将代码行①和②对换位置，后序遍历就是①和③调换位置。

*非递归实现

虽然递归实现很简洁明了，但面试官通常喜欢要求实现非递归遍历。非递归遍历也有很多种方法，最常见最容易想到的就是用栈模拟递归。

写法如下，都是在栈和节点指针有一个不为空的时候循环，如果p不空，压栈，并访问左节点，如果p空，弹栈，并指向栈顶结点的右节点。后序遍历有点不同，需要将结点进行两次弹出，第一次弹出的时候并不真正的弹出，第二次弹出才真的弹出。

void preOrder(treenode p){
  stack<element> s;
  while(p||!s.empty()){
    if(p){
        cout << p->val;
        s.push(p);
        p = p->left;
    }else{
        p = s.top();
        p = p->right;
        s.pop();
    }      
  }
}
/**************/
void inOrder(treenode p){
  stack<element> s;
  while(p||!s.empty()){
    if(p){
        s.push(p);
        p = p->left;
    }else{
        p = s.top();
        cout << p->val;
        p = p->right;
        s.pop();
    }      
  }
}
/**************/
void postOrder(treenode p){
  stack<element> s;
  while(p||!s.empty()){
    if(p){
        s.push(p);
        p = p->left;
    }else{
        p = s.top();
        s.pop();
        p->times++;
        if(p->times==1){
          s.push(p);
          p=p->right;
        }else{
          cout<< p->val;
          p = nullptr;
        } 
}}}

层序遍历

除了以上三种，还有一种遍历方式是层序遍历，即从上至下逐层，每层从左至右的遍历。层序遍历采用队列实现，根节点入队，根节点出队的同时，让根节点的左右结点依次入队，后面依次出队，每个出队的结点都将自己的左右儿子入队，直到队列为空，遍历完成。

总结：遍历一般有两种，DFS深度优先和BFS广度优先，后面图章节会讲到。在树中，前中后序遍历属于深度优先搜索，层序遍历属于广度优先搜索。