Loading

编译原理：LL1、LR0、SLR1、LR1、LALR1

1 FIRST&FOLLOW

1.1 FIRST集合

First(α) 是可从 α 推导得到的句型的首终结符号的集合

image-20210116145324190

计算FIRST(X)集合算法：

  • 计算每个符号X的First(X)集合
image-20210116150338983

  • 计算每个符号串 α 的 First(α) 集合

    image-20210116150518674

1.2 FOLLOW集合

Follow(A) 是可能在某些句型中紧跟在 A 右边的终结符的集合

image-20210116150204396

计算FOLLOW(X)集合算法：

  • 为每个非终结符 X 计算 Follow(X) 集合

    image-20210116150743310

2 LL(1)

如果文法 G 的预测分析表是无冲突的, 则 G 是 LL(1) 文法

对于当前选择的非终结符, 仅根据输入中当前的词法单元即可确定需要使用哪条产生式

预测分析表指明了每个非终结符在面对不同的词法单元或文件结束符时, 该选择哪个产生式 (按编号进行索引) 或者报错

  • L : 从左向右 (left-to-right) 扫描输入
  • L : 构建最左 (leftmost) 推导
  • 1 : 只需向前看一个输入符号便可确定使用哪条产生式

2.1 构建预测分析表

先计算FIRST、FOLLOW集合

image-20210116152100751

注：或者关系，两者都要检查！

例子：

image-20210116152249859

2.2 改造为LL(1)

2.2.1 提取左公因子

image-20210116153257570

2.2.2 消除左递归

  • 直接左递归的消除方法：

    image-20210116152611509

    例如：

    E → E + T | T

    消除后为：

    E → T E′

    E ′ → + T E′ | ϵ

  • 非直接左递归

    思想：无环图

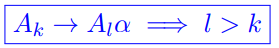
    image-20210116153035174

    image-20210116153044330

    例子：

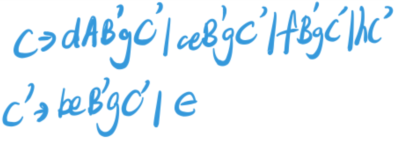
    image-20210116153215385 image-20210116153234519

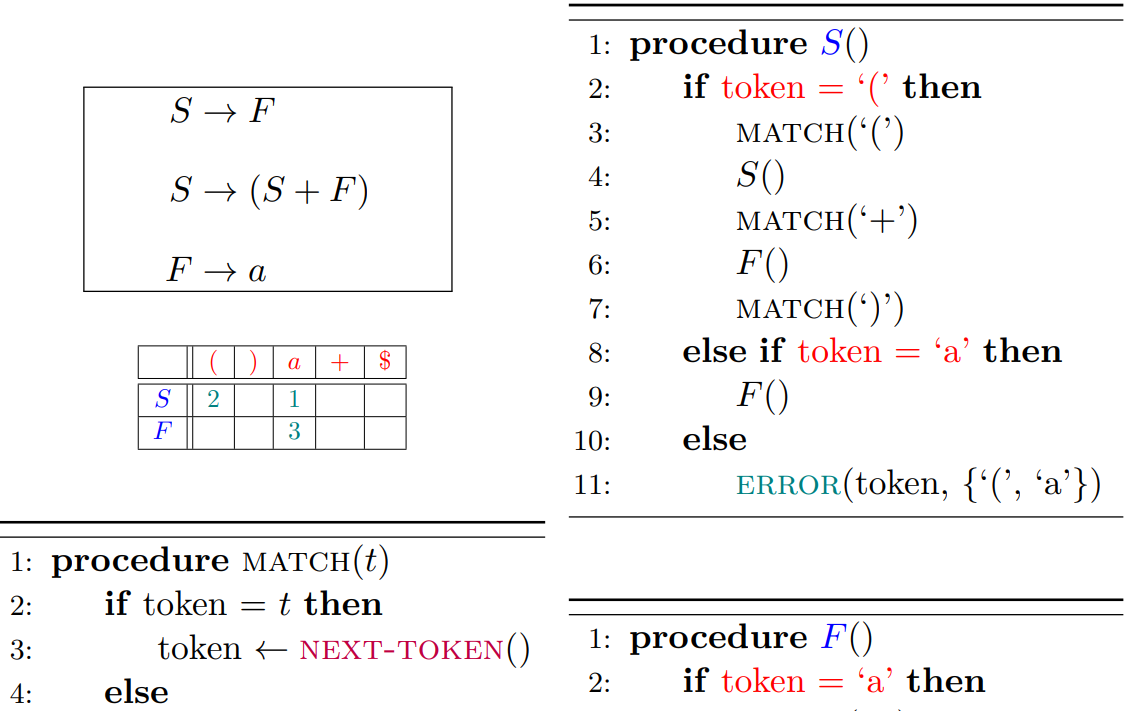
2.3 LL(1)语法分析器伪代码

image-20210116145239560

3 LR

3.1 什么是LR

L : 从左向右 (Left-to-right) 扫描输入

R : 构建反向 (Reverse) 最右推导

image-20210116154534821

两大操作: 移入输入符号 与 按产生式归约

主要问题：

  • 何时规约？
  • 按哪条产生式规约？

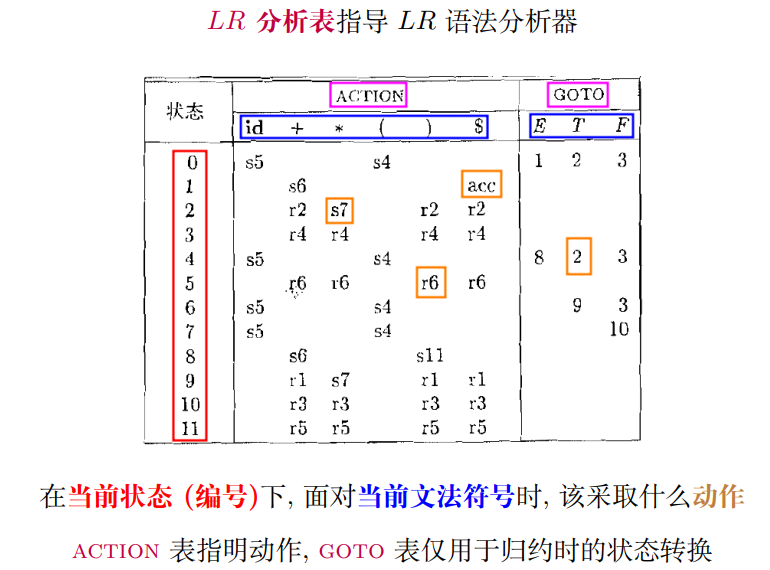
3.2 LR分析表

image-20210116154817549 image-20210116154852959

  • 例子：栈上的移入与规约

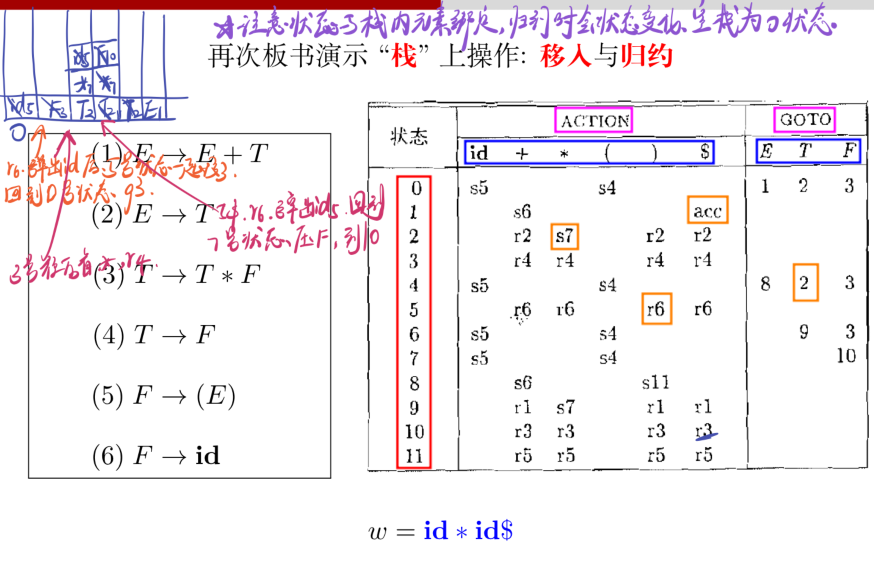
    image-20210116161844367

  • 问题：在当前状态 (编号)下, 面对当前文法符号时, 该采取什么动作

    思路：可以用自动机跟踪状态变化 (自动机中的路径 ⇔ 栈中符号/状态编号)

  • 何时规约？

    必要条件: 当前状态中, 已观察到某个产生式的完整右部，也就是句柄

    Definition (句柄 (Handle))

    在输入串的 (唯一) 反向最右推导中, 如果下一步是逆用产生式 A → α 将 α 归约为 A, 则称 α 是当前句型的句柄。

    image-20210116155640688

  • Theorem 存在一种 LR 语法分析方法, 保证句柄总是出现在栈顶

4 LR(0)

4.1 LR(0)文法

如果文法G的LR(0)分析表是无冲突的，则G是LR(0)文法

无冲突：ACTION表中每个单元格最多只有一种操作

  • L : 从左向右 (Left-to-right) 扫描输入

  • R : 构建反向 (Reverse) 最右推导

  • 0 : 归约时无需向前看

4.2 LR(0)自动机

Definition (LR(0) 项 (Item))

文法 G 的一个 LR(0) 项是 G 的某个产生式加上一个位于体部的点

项指明了语法分析器已经观察到了某个产生式的某个前缀

image-20210116155852780

Definition (项集)

项集就是若干项构成的集合

句柄识别自动机的一个状态可以表示为一个项集

Definition (项集族)

项集族就是若干项集构成的集合

句柄识别自动机的状态集可以表示为一个项集族

Definition (增广文法 (Augmented Grammar))

文法 G 的增广文法 G′ 是在 G 中加入产生式 S ′ → S 得到的文法

目的: 告诉语法分析器何时停止分析并接受输入符号串

当语法分析器面对 $且要使用 S ′ → S 进行归约时, 输入符号串被接受

Example：LR(0) 句柄识别自动机（红圈表示接受状态）

image-20210116160058568

4.3 构造LR(0)自动机

需要知道的：闭包的计算

image-20210116160544085

  • init

    image-20210116160621662

  • 演化

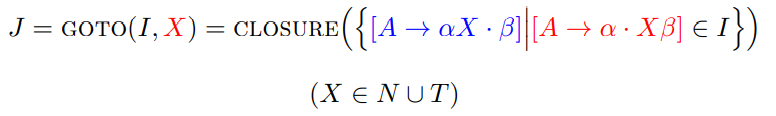
    image-20210116160734039 image-20210116160645402

  • 接受状态

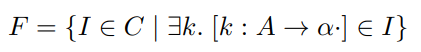
    image-20210116160754703

  • accept状态

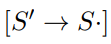
    image-20210116161533524

    下，遇见$的转移

    千万不要漏掉accept！

4.4 构造LR(0)分析表

  1. 先构造出LR(0)自动机，每个自动机的状态对应LR(0)分析表中的一个状态

  2. 根据以下规则，构造LR(0)分析表

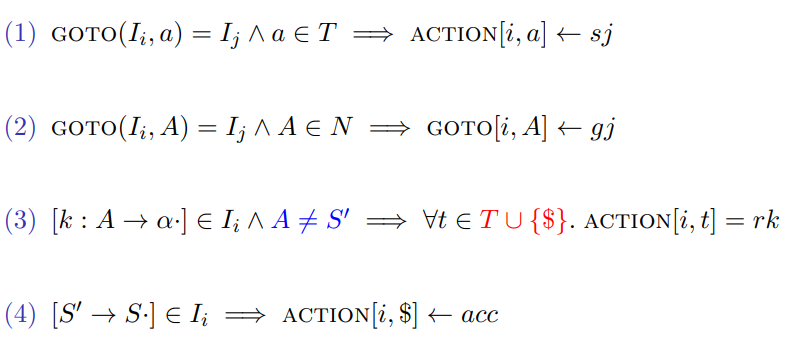
    image-20210116161228528

  3. 如果文法 G 的LR(0) 分析表是无冲突的, 则 G 是 LR(0) 文法

5 SLR(1)

Simple LR(1)

5.1 LR(0)存在的问题

LR(0) 分析表每一行 (状态) 所选用的归约产生式是相同的

5.2 改进

对LR(0)的规约规则进行改进

image-20210116163930031

6 LR(1)

6.1 LR(0)与SLR(1)存在的问题

  • LR0

    image-20210116163530517

  • SLR1

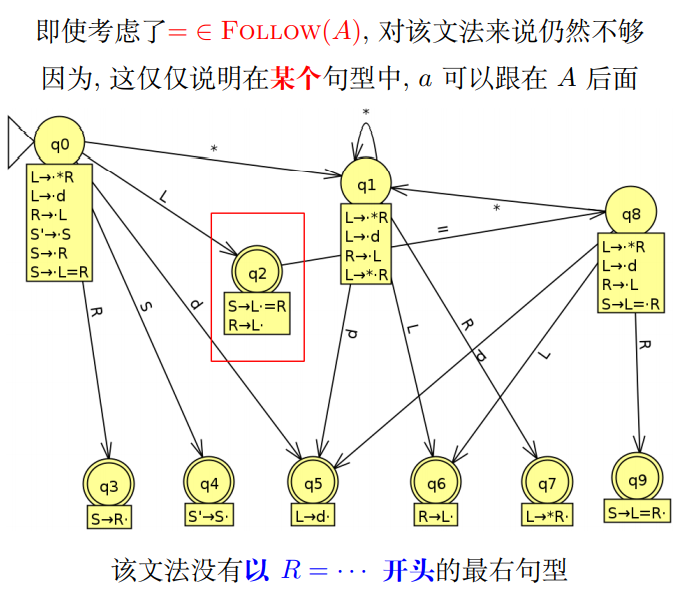
    image-20210116164433903

6.2 LR(1)项

Definition (LR(1) 项 (Item))

[A → α · β, a] (a ∈ T ∪ {$}) 此处, a 是向前看符号, 数量为 1

思想: α 在栈顶, 且剩余输入中开头的是可以从 βa 推导出的符号串

也就是说，[A → α·, a]只有下一个输入符号为 a 时, 才可以按照 A → α 进行归约

6.3 LR(1)自动机

  • LR1闭包计算

    image-20210116164646724

  • LR1初始化

    image-20210116164709796

  • LR1的GOTO计算

    image-20210116164727388

  • LR1自动机构造

    image-20210116164748274

6.4 LR(1)分析表

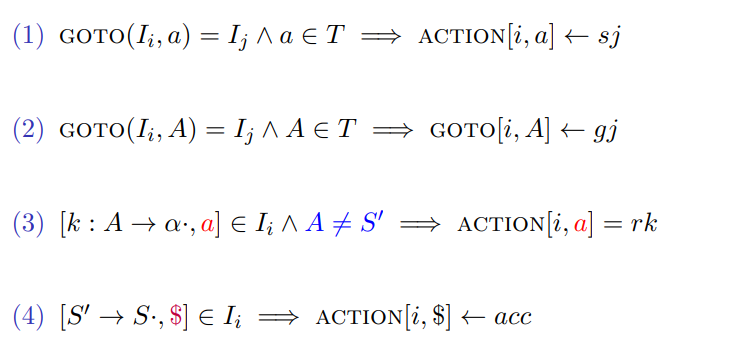
image-20210116170629909

7 LALR(1)

7.1 LR(1)的问题

LR(1) 虽然强大, 但是生成的 LR(1) 分析表可能过大, 状态过多

LALR(1) : 合并具有相同核心 LR(0)项的状态 (忽略不同的向前看符号)

7.2 合并核心项

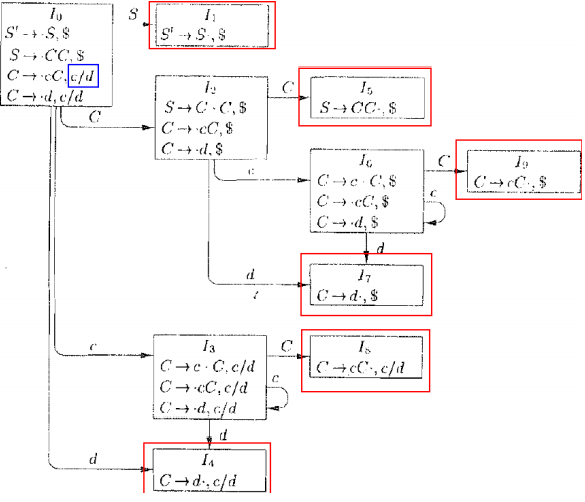
image-20210116171016290

例如，合并图中的(4,7),(3,6),(8,9)

7.3 引入冲突？

对于 LR(1) 文法, 合并得到的 LALR(1) 分析表是否会引入冲突？

  • 不会引入移入/归约冲突

    假设合并后出现冲突，[A → α·, a] 与 [B → β · aγ, b]

    则在 LR(1) 自动机中, 存在某状态同时包含 [A → α·, a] 与 [B → β · aγ, c] (c随便是什么)

  • 可能会引入归约/归约冲突

8 例题

8.1 LR0、SLR1

image-20210116232017203

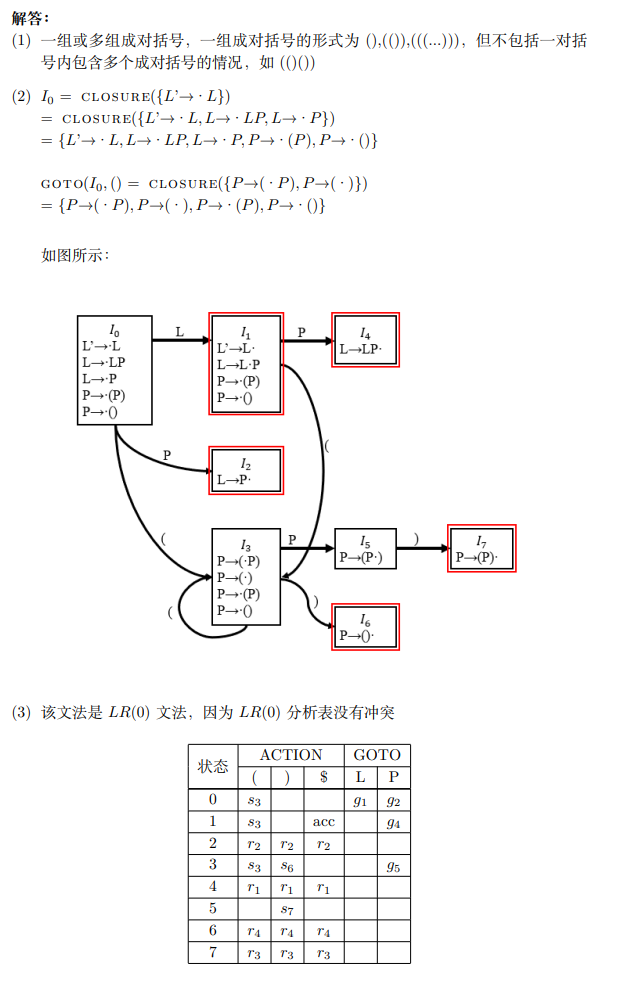
image-20210116232034684

image-20210116232041655

8.2 LR1、LALR1

image-20210116232100595

image-20210116232108019

image-20210116232114937

posted @ 2021-01-16 23:17  cpaulyz  阅读(8631)  评论(0)  编辑  收藏  举报