06线性回归算法原理推导

通过年龄，工资。预测贷款金额。

贷款金额： = k1 * 工资 + k2 * 工资  + k   k1 ，k2 权重对结果影响大， k 偏置项对结果影响小

化简整合：多少个特征，就有多少个权重参数

 

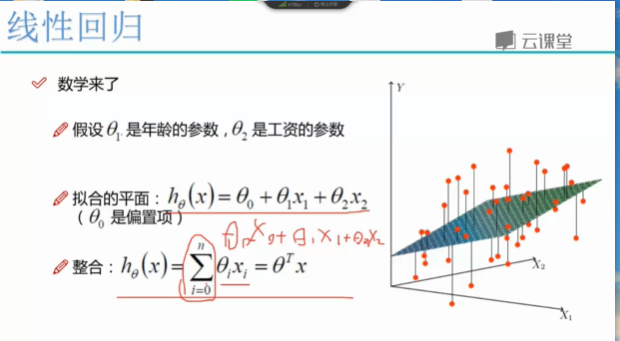
 额外增加一列： 值为1 . 为了矩阵计算。

真实值和预测值之间存在差异。理论模型和现实模型必然存在差异。

每个样本： 真实值 = k * 样本 + 误差

误差： 一万个样本有一万个误差。 误差是对立分布，并且具有相同分布。并且服从均值为0方差为x*x 的高斯分布。

独立：每个样本没有关系

同分布： 在一个环境

高斯分布： 特点均值为零，方差为k2。

机器学习： 做了假设，获得的模型是可利用的。就认为模行是可以的。

 

求 θ 。

似然函数： 什么样参数更我们的数据组合恰好是真实值。

赌场： 10个人进去，9个人赢钱。1 个人输钱。第11个人有90%会赢钱。

用数据推参数等于什么，就是似然函数。极大似然函数，最大似然函数。最大似然估计。

考虑所有的样本，加法问题容易，乘法太难。

对数似然：乘法 将乘法转化为加法。

 

 

 

 让预测值成为真实值越大越好。

 

 

求最大值问题转化为最小值问题。θ 不是都能求解的。

 

 

 

评估方法： R*R ==1 最好， RR == 0 不好

残差： 预测值和真实值的差

方差项：预测值和 平均值