蒙特卡洛法
蒙特卡洛（Monte Carlo）法是一类随机算法的统称。随着二十世纪电子计算机的出现，蒙特卡洛法已经在诸多领域展现出了超强的能力。在机器学习和自然语言处理技术中，常常被用到的MCMC也是由此发展而来。本文通过蒙特卡洛法最为常见的一种应用——求解定积分，来演示这类算法的核心思想。
无意识统计学家法则（Law of the unconscious statistician）
这是本文后续会用到的一个定理。作为一个预备知识，我们首先来介绍一下它。
LOTUS的意思是：已知随机变量X的概率密度函数为，但不知道g(X)的概率分布，此时用LOTUS公式能计算出函数g(X)的数学期望。LOTUS的公式如下：
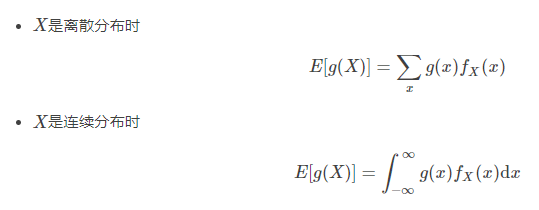
其实就是在计算期望时，用已知的X的PDF（或PMF）代替未知的g(X)的PDF（或PMF）。
蒙特卡洛求定积分（一）：投点法
这个方法也常常被用来求π值。现在我们用它来求函数的定积分。如下图所示，有一个函数f(x)，若要求它从a到b的定积分,其实就是求曲线下方的面积。这时我们可以用一个比较容易算得面积的矩型罩在函数的积分区间上（假设其面积为Area）。然后随机地向这个矩形框里面投点，其中落在函数，f(x)下方的点为绿色，其它点为红色。然后统计绿色点的数量占所有点（红色+绿色）数量的比例为r，那么就可以据此估算出函数f(x)从a到b的定积分为Area * r。
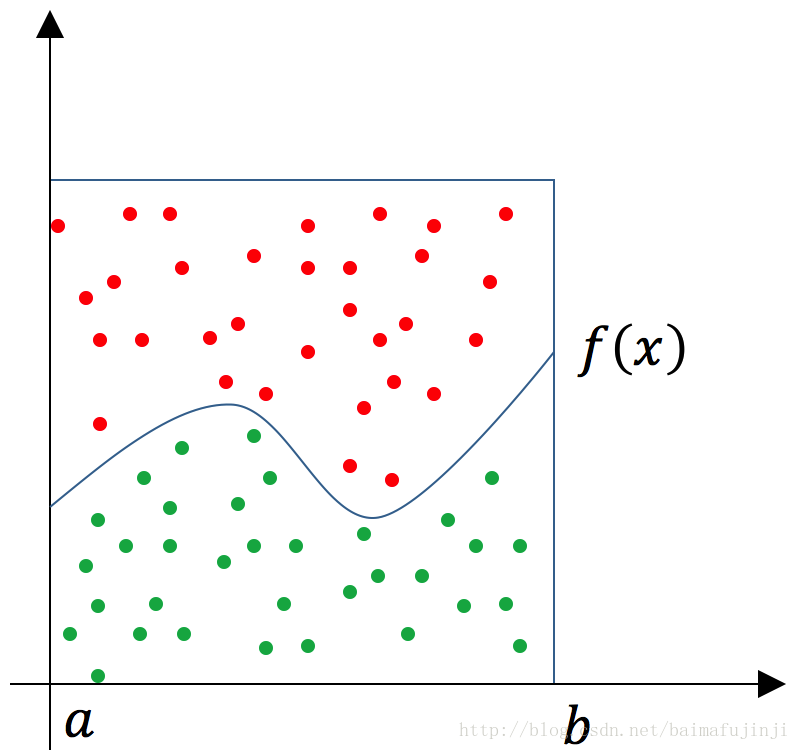
注意由蒙特卡洛法得出的值并不是一个精确值，而是一个近似值。而且当投点的数量越来越大时，这个近似值也越接近真实值。
蒙特卡洛求定积分（二）：期望法
下面我们来重点介绍一下利用蒙特卡洛法求定积分的第二种方法——期望法，有时也成为平均值法。
任取一组相互独立、同分布的随机变量{}，
在[a, b]上服从分布律
，也就是说
是随机变量X的PDF（或PMF）。令
，则
也是一组独立同分布的随机变量，而且
由强大数定理
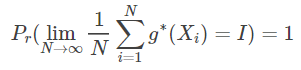
若选
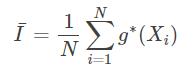
则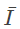
依概率1收敛于I，则可以把平均值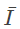作为期望I的近似值。
假设要计算的积分有如下形式
其中被积函数g(x)在区间[a, b]内可积。任意选择一个有简便办法可以进行抽样的概率密度函数，使其满足下列条件
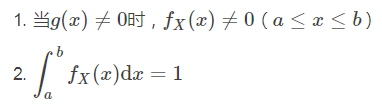
如果记
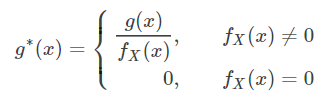
那么原积分可以写作
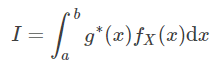
因而求积分的步骤是：
如果a, b为有限值，那么可取作为均匀分布：
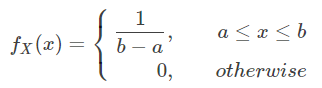
此时原来的积分式变为
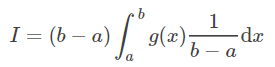
具体步骤如下：
平均值法的直观解释
下面是来自参考文献【1】的一个例子。注意积分的几何意义就是[a,b]区间内曲线下方的面积。
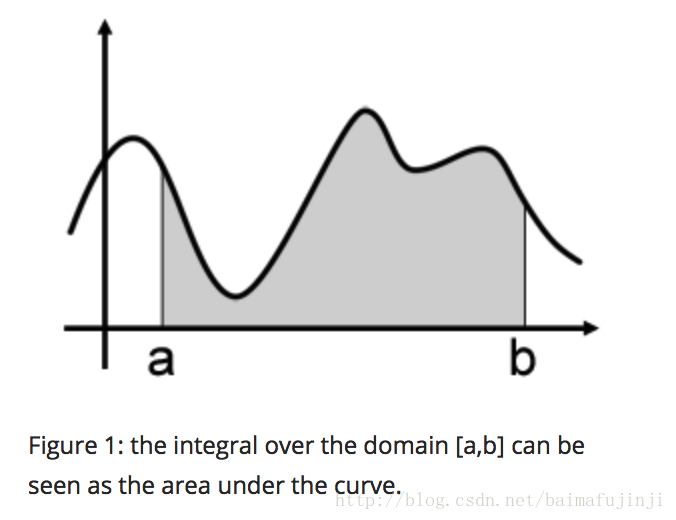
当我们在[a,b]之间随机取一点x时，它对应的函数值就是f(x)，然后变可以用f(x) * (b - a)来粗略估计曲线下方的面积（也就是积分），当然这种估计（或近似）是非常粗略的。
于是我们想到在[a, b]之间随机取一系列点xi时（xi满足均匀分布），然后把估算出来的面积取平均来作为积分估计的一个更好的近似值。可以想象，如果这样的采样点越来越多，那么对于这个积分的估计也就越来越接近。
按照上面这个思路，我们得到积分公式为
注意其中的1/(b - a)就是均匀分布的PDF。这跟我们之前推导出来的蒙特卡洛积分公式是一致的。
1. PDF：概率密度函数（probability density function）, 在数学中，连续型随机变量的概率密度函数（在不至于混淆时可以简称为密度函数）是一个描述这个随机变量的输出值，在某个确定的取值点附近的可能性的函数。本身不是概率，取值积分后才是概率。
2. PMF: 概率质量函数（probability mass function), 在概率论中，概率质量函数是离散随机变量在各特定取值上的概率。
3. CDF: 累积分布函数 (cumulative distribution function)，又叫分布函数，是概率密度函数的积分，能完整描述一个实随机变量X的概率分布。是PDF在特定区间上的积分。CDF就是PDF的积分，PDF就是CDF的导数。
转自：https://blog.csdn.net/baimafujinji/article/details/53869358
