贝叶斯公式深入理解
独立同分布随机事件
对于n次独立同分布随机事件实验，我们如何计算随机事件概率？举个例子，我们抛同一枚硬币100次，出现正面52次，反面48次，那抛硬币正面的概率是多少？
频率派思想
频率派认为事件A的概率（如例子中抛硬币出现正面的概率）是确定的，只是我们不知道，当进行大量重复实验后，事件A发生的概率大致上等于实验中A发生的频率，这也是大数定律的思想。如下，μ表示事件A出现次数的期望
实际应用中，我们难以进行大量重复事件，但频率派认为，我们有理由相信当前的实验结果是在概率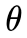
下最有可能出现的结果。似然函数表示出现当前实验结果的概率函数
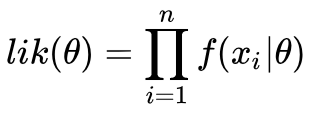
x为实验结果已知，我们求出极值点下的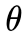
值，则求出了最大似然概率，频率派即用
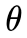表示事件A的概率。
频率派思想是自然而然的思想，我们在生活中也不经意间使用。例如上面例子，我们有
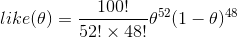
两边取对数
极值点下对
求导等于0，很容易计算出
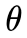为0.52。可以看到，最大化似然函数得到的概率
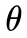和直接使用大数定律一致。
贝叶斯思想
贝叶斯认为，由于我们的实验次数永远不会无穷，所以我们不应该给出
确定的值。就像上述例子中，仅仅进行了100次实验，概率派则认为抛硬币出现正面的概率为0.52，这是荒谬的。0.52和大数定律的结果一致，但是100次显然距离无穷太远。（实际上频率派引入了置信度，他们并不认为0.52是正确值，0.52在一定概率下是正确的）
所以，贝叶斯提出了贝叶斯公式，他认为，在我们有限的观察次数下，事件A出现的概率应该服从一定的概率分布。在上述例子中，贝叶斯认为抛硬币出现正面概率为0.5左右的可能性为0.8，但是抛硬币出现正面得概率为0.2或0.8的概率可能还有0.2（这里的概率大概写的，不要当真）。贝叶斯公式如下
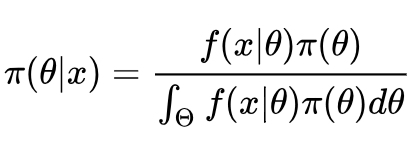
离散情况下，贝叶斯公式这样表示
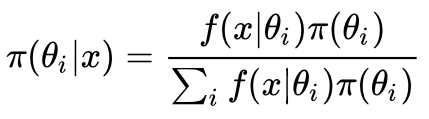
这里，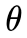
表示目标概率（我们想要得到的事件概率），
表示实验前目标概率的概率分布（先验概率分布），
表示实验后目标概率的概率分布（后验概率分布），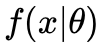
表示实验中得到的事件概率（
使用似然函数计算）。再次强调，贝叶斯想要计算的是概率的概率分布。
第n次实验的后验概率为第n + 1次实验的先验概率，首次实验开始之前的先验概率函数可以根据经验设定，如果没有经验可以参考，我们不妨假设
服从均匀分布，即
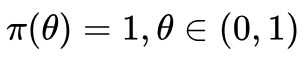
实际上，当进行的重复实验足够多，最初的先验概率对最终的结果影响较小。
这里可以看到贝叶斯思想的另外一个精髓，贝叶斯概率的概率分布随着实验的进行不断波动，并且随着实验次数的增加，概率的概率分布将会慢慢收敛，最终满足大数定律。
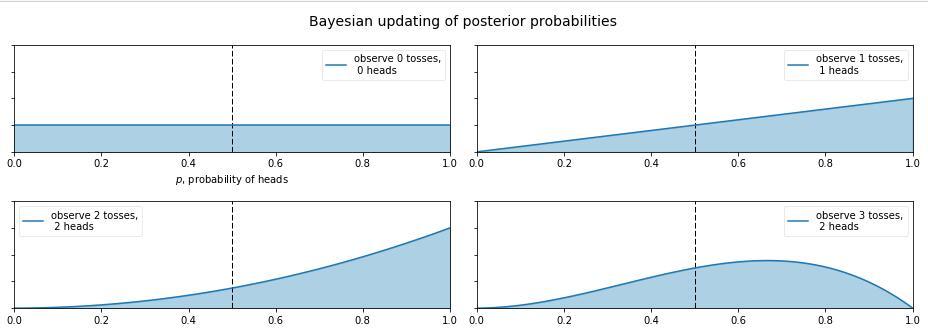
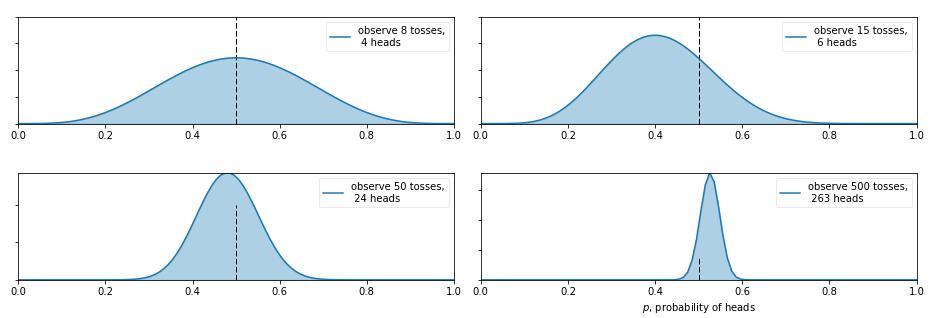
上图表示随着抛硬币实验的不断进行，后验概率分布图像的变化。
贝叶斯思想的优势
1、 对于某一种独立重复随机事件，如果采用最大似然法计算出两个极值点，例如99、100，此时最大似然法只会取最大值点100的概率值。但是使用贝叶斯思想，我们就可以同时考虑极值点99、100的概率。
在实际应用中，事件A的概率可能不是一成不变的（实验难以重复独立，或者事件A的概率就是随机的）。比如考虑一个人生病的概率，幼年时生病概率高，中年时生病概率低，老年时生病概率高，或者冬天生病概率高，夏天生病概率低。频率派思想认为的概率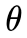
是事件A的固定属性在这些状况下就不适用。严格的来说，任何场景下你都无法保证事件A概率
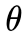是固定的。
2、 频率派使用的最大似然法，只能得到概率的最大似然估计。但是通过贝叶斯公式得到概率后验分布函数后，我们可以进行各种处理，比如取概率期望，概率中位数，概率极大值等等。
3、 下面的章节我们还可以看到基于贝叶斯公式的共轭分布，他对于后验概率的计算十分方便，这也是贝叶斯公式的一大优势。
参考：
https://www.zhihu.com/question/21134457
