Gamma函数深入理解

Gamma函数

当n为正整数时，n的阶乘定义如下：n! = n * (n - 1) * (n - 2) * … * 2 * 1。

当n不是整数时，n!为多少？我们先给出答案。

 

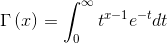
容易证明，Γ(x + 1) = x * Γ(x)，当n为正整数时，显然有Γ(n) = (n – 1)!。

计算(1/2)!

先给一个神奇的公式，证明不详述。

（1）

定义如下函数

 

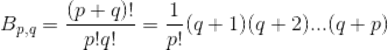
令上式p = 1，q = 1/2，同时根据对称性原理，有

（2）

 

同时容易证明

（3）

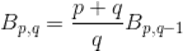
令p = 1/2，结合（2）（3）式，有

 

 

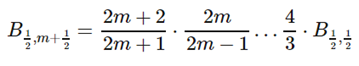
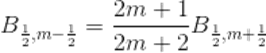
由于B关于q递增，则

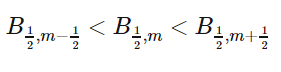
对m取极限，有

 

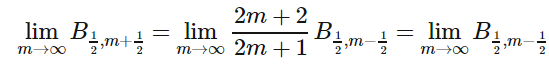
根据夹逼定理，则

 

即

 

结合公式（1），有

 

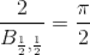
即

 

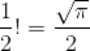
n!的通用公式

整数n!序列如下

n	1	2	3	4	5
n!	1	2	6	24	120

我们把这些点用光滑曲线连接起来，得到如下图形

 

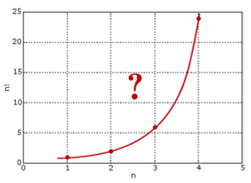
求n!的通用公式，即求该曲线的函数表达式。由于需要把阶乘推广到实数，所以最终求得的函数中不能包含阶乘运算。

 

欧拉最终解决了n!通用公式的问题，他通过研究如下函数找到了解决办法

 

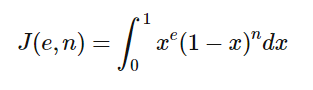
此处 n 为正整数，e 为正实数。利用分部积分法，很容易证明

 

连续使用上面递推公式，有

 

于是欧拉得到如下重要公式。

 

欧拉应用各种参数替换数学技巧与极限思想，成功推导出Gamma函数。

 

Gamma函数图像如下

 

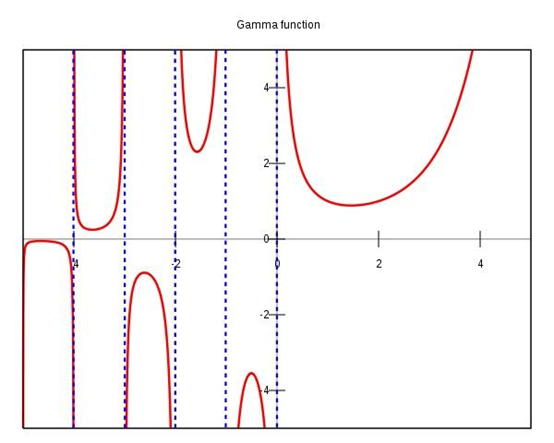
Gamma函数的应用

由于Gamma函数在实数域具有阶乘性质：Γ(x + 1) = x * Γ(x)，所以可以把很多具有阶乘性质得自然数应用推广到实数域，离散特性推广为连续特性。比如对函数的整数次求导推广到实数次求导，二项分布推广为Beta分布。Gamma函数与泊松分布等共轭，Gamma函数在数论以及高维空间计算球体积中也有应用。

 

参考：

http://www.flickering.cn/%E6%95%B0%E5%AD%A6%E4%B9%8B%E7%BE%8E/2014/06/%E7%A5%9E%E5%A5%87%E7%9A%84%E4%BC%BD%E7%8E%9B%E5%87%BD%E6%95%B0%E4%B8%8A/

http://www.flickering.cn/%E6%95%B0%E5%AD%A6%E4%B9%8B%E7%BE%8E/2014/07/%E7%A5%9E%E5%A5%87%E7%9A%84%E4%BC%BD%E7%8E%9B%E5%87%BD%E6%95%B0%E4%B8%8B/