决策树算法——ID3
决策树算法是一种有监督的分类学习算法。利用经验数据建立最优分类树,再用分类树预测未知数据。
例子:利用学生上课与作业状态预测考试成绩。
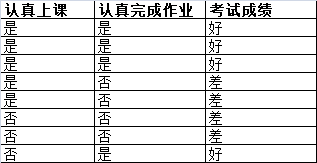
上述例子包含两个可以观测的属性:上课是否认真,作业是否认真,并以此预测考试成绩。针对经验数据,我们可以建立两种分类树
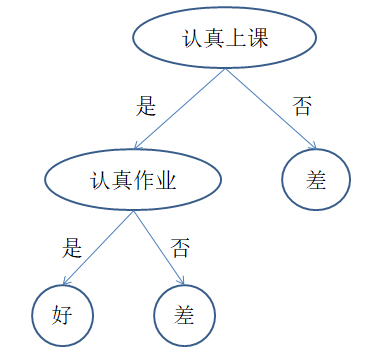
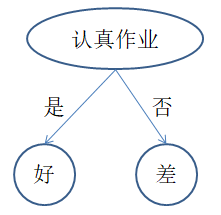
两棵树都能对经验数据正确分类,实际上第二棵树更好,原因是什么呢?在此,我们介绍ID3分类算法。
1、信息熵
例如,我们想要获取球队比赛胜负的信息:中国队vs巴西队、中国队vs沙特队。
哪场比赛信息量高?答案是中国队vs沙特队。原因是中国队vs沙特队输赢的确定性小于中国队vs巴西队输赢的确定性。
假设样本集合是D,其中第k类样本所占的比例为pk,则D的信息熵为
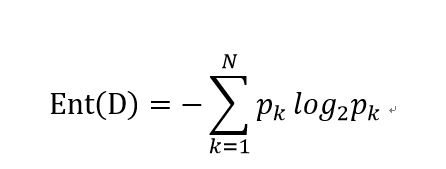
假设中国队vs巴西队输的概率为80%,则信息量Ent = -0.8 * log2(0.8) - 0.2 * log2(0.2) = 0.722。
假设中国队vs沙特队输的概率为50%,则信息量Ent = -0.5 * log2(0.5) - 0.5 * log2(0.5) = 1。
我们可以看出来,不确定性越高的场景包含越多的信息量。
2、信息增益
实际应用中,单独使用信息熵的情况比较少,往往使用信息熵的增益来指导工作。
基于信息熵,我们可以对某个属性a定义"信息增益"
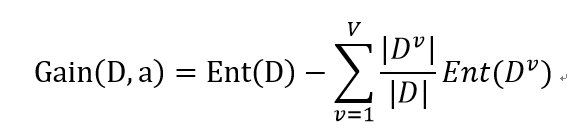
其中,a属性有V个可能取值,而D中在属性a上取值为的样本记为Dv。
比如我们买足彩竞猜两支球队的输赢,我们可以获得两个消息中的一个:比赛球队是哪两个球队,比赛日期是哪一天。你愿意获取哪一个消息?相信大部分人都会选择前一个消息。原因很简单,前一个消息对于我们预测输赢的帮助高于后一个消息。
在我们没有任何额外信息的情况下,两支球队的输赢为50%。但是当我们知道了球队名称后,我们可以根据他们的FIFA排名来预测输赢。FIFA排名高的赢得概率更高。仅仅知道比赛日期可能对于我们的预测没有太大帮助。
比如我们知道了是中国队vs巴西队的比赛,则信息增量为1-0.722 = 0.278。
3、ID3算法原理
每次分类,我们选取信息增益最大的属性进行分类,然后进行递归分类。
对于文章开始的例子,初始信息熵为Ent = -0.5 * log2(0.5) - 0.5 * log2(0.5) = 1。
选择认真上课属性后,信息熵Ent(认真上课) = -5/8 * ((3/5 * log2(3/5) - 2/5 * log2(2/5)) - 3/8 * ((1/3 * log2(1/3) - 2/3 * log2(2/3)) = 0.951,信息增益为0.049。
选择认真作业属性后,信息熵Ent(认真作业) = -4/8 * ((1 * log2(1) - 0 * log2(0)) - 4/8 * ((1 * log2(1) - 0 * log2(0)) = 0,信息增益为1。
所以选择认真作业属性更优。
4、实例
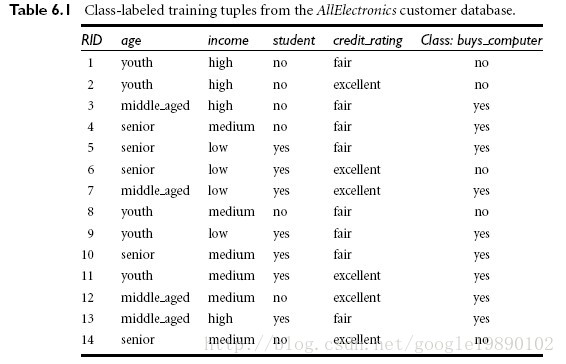
根据年龄,身份,收入,信用预测买电脑的情况。java代码如下
package com.coshaho.learn.detree; import java.util.ArrayList; import java.util.HashMap; import java.util.List; import java.util.Map; /** * * ID3Tree.java Create on 2018年6月19日 上午12:29:06 * * 类功能说明: ID3 决策树算法 * * Copyright: Copyright(c) 2013 * Company: COSHAHO * @Version 1.0 * @Author coshaho */ public class ID3Tree { public void createTree(String[] feature, int[][] data) { Node root = new Node(); root.setParent(null); root.setFeature("root"); root.setValue(-1); root.setLevel(0); bestFit(feature, data, root, 0); System.out.print(root); } /** * 选择最优属性(获得信息量最大的属性) * @author coshaho * @param feature * @param data * @param parent * @param level */ public void bestFit(String[] feature, int[][] data, Node parent, int level) { if(!validateData(data)) { Node me = new Node(); me.setLevel(level + 1); me.setFeature("class"); me.setParent(parent); me.setValue(data[0][data[0].length - 1]); parent.getChildren().add(me); return; } int m = data.length; int n = data[0].length; int featureNum = n - 1; // 计算当前信息量 double oldEntropy = calEntropy(data); double gainEntropy = -1d; int bestFeature = 0; Map<Integer, int[][]> nextData = null; for(int i = 0; i < featureNum; i++) { double newEntropy = 0.0d; Map<Integer, int[][]> splitData = splitData(data, i); // 按照某属性分类后的信息量 for(Map.Entry<Integer, int[][]> entry : splitData.entrySet()) { double entropy = calEntropy(entry.getValue()); newEntropy = newEntropy + entropy * entry.getValue().length / m; } // 选取信息量获取最大的属性分类 if(oldEntropy - newEntropy > gainEntropy) { gainEntropy = oldEntropy - newEntropy; bestFeature = i; nextData = splitData; } } String[] nextFeature = removeBestFeature(feature, bestFeature); // 递归分解 for(Map.Entry<Integer, int[][]> entry : nextData.entrySet()) { Node me = new Node(); me.setFeature(feature[bestFeature]); me.setParent(parent); me.setValue(entry.getKey()); me.setLevel(level + 1); parent.getChildren().add(me); bestFit(nextFeature, entry.getValue(), me, level + 1); } } /** * 移除已经分类的属性 * @author coshaho * @param feature * @param index * @return */ private String[] removeBestFeature(String[] feature, int index) { String[] result = new String[feature.length - 1]; boolean flag = true; for(int j = 0; j < feature.length; j++) { if(index == j) { flag = false; continue; } if(flag) { result[j] = feature[j]; } else { result[j - 1] = feature[j]; } } return result; } /** * 计算信息熵 * Entropy = -sigma(u * log2(u)) * @author coshaho * @param data * @return */ private double calEntropy(int[][] data) { int m = data.length; int n = data[0].length; Map<Integer, Integer> map = new HashMap<Integer, Integer>(); for(int i = 0; i < m; i++) { map.put(data[i][n-1], null == map.get(data[i][n-1]) ? 1 : map.get(data[i][n-1]) + 1); } double result = 0.0d; for(Map.Entry<Integer, Integer> entry : map.entrySet()) { result = result - (double)entry.getValue() / m * Math.log((double)entry.getValue() / m) / Math.log(2); } return result; } /** * 按照属性index进行数据聚类 * @author coshaho * @param data * @param index * @return */ private Map<Integer, int[][]> splitData(int[][] data, int index) { int m = data.length; int n = data[0].length; // 数据划分:删除某列属性值并按照这列属性划分数据 Map<Integer, List<int[]>> map = new HashMap<Integer, List<int[]>>(); for(int i = 0; i < m; i++) { int key = data[i][index]; int[] v = new int[n - 1]; boolean flag = true; for(int j = 0; j < n; j++) { if(index == j) { flag = false; continue; } if(flag) { v[j] = data[i][j]; } else { v[j - 1] = data[i][j]; } } if(map.containsKey(key)) { map.get(key).add(v); } else { List<int[]> list = new ArrayList<int[]>(); list.add(v); map.put(key, list); } } // 数据格式转换 Map<Integer, int[][]> result = new HashMap<Integer, int[][]>(); for(Map.Entry<Integer, List<int[]>> entry : map.entrySet()) { List<int[]> v = entry.getValue(); int[][] value = new int[v.size()][]; v.toArray(value); result.put(entry.getKey(), value); } return result; } /** * 数据校验 * @author coshaho * @param data * @return */ private boolean validateData(int[][] data) { if(1 == data.length || 1 == data[0].length) { return false; } int m = data.length; int n = data[0].length; int classOne = 1; for(int i = 1; i < m; i++) { if(data[i][n - 1] == data[0][n - 1]) { classOne++; } } if(m == classOne) { return false; } return true; } public static class Node { private Node parent; private List<Node> children = new ArrayList<Node>(); private int value; private String feature; private int level; public int getLevel() { return level; } public void setLevel(int level) { this.level = level; } public Node getParent() { return parent; } public void setParent(Node parent) { this.parent = parent; } public List<Node> getChildren() { return children; } public void setChildren(List<Node> children) { this.children = children; } public int getValue() { return value; } public void setValue(int value) { this.value = value; } public String getFeature() { return feature; } public void setFeature(String feature) { this.feature = feature; } public String toString() { String result = blank() + feature + ":" + value + "\n"; for(Node node : children) { result = result + node.toString(); } return result; } private String blank() { StringBuffer sb = new StringBuffer(); for(int i = 0; i < level; i++) { sb.append("--"); } return sb.toString(); } } public static void main(String[] args) { int[][] data = {{0,2,0,0,0}, {0,2,0,1,0}, {1,2,0,0,1}, {2,1,0,0,1}, {2,0,1,0,1}, {2,0,1,1,0}, {1,0,1,1,1}, {0,1,0,0,0}, {0,0,1,0,1}, {2,1,1,0,1}, {0,1,1,1,1}, {1,1,0,1,1}, {1,2,1,0,1}, {2,1,0,1,0}}; String[] feature = {"age", "income", "student", "credit", "class"}; new ID3Tree().createTree(feature, data); } }
运行结果
root:-1 --age:0 ----student:0 ------class:0 ----student:1 ------class:1 --age:1 ----class:1 --age:2 ----credit:0 ------class:1 ----credit:1 ------class:0



 浙公网安备 33010602011771号
浙公网安备 33010602011771号