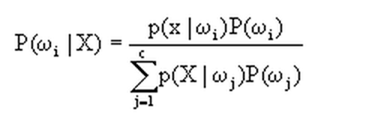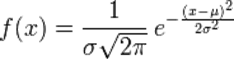基于最小错误率的贝叶斯决策
理论上的东西,就不写了,也写不出什么有价值的东西,资料太多了。后文很多关于原理的讲述都给出了其他文章的引用。
分享一个比较简单易懂的贝叶斯决策理论与统计判别方法。
数据集:
328 个同学的身高、体重、性别数据(78 个女生、250 个男生)
124 个同学的数据(40 女、84 男)
90 个同学的数据(16 女,74 男)
问题描述:
以dataset1为训练数据库,假设身高与体重满足高斯分布,进行高斯分布的参数估计,并进行基于最小错误率的贝叶斯分类,分别考虑男女的先验概率,0.5-0.5;0.6-0.4;0.7-0.3,0.8-0.2,并以dataset2和dataset3为测试数据库分析分类性能,并探讨先验概率对分类性能的影响
需要解决的问题:
通过文章开头提供的资料可以看出,其实判别的函数就是下图,就是给定一个待测向量X,它是类别Wi的概率。
等号右边,P(Wi)就是先验概率,而p(X|Wi)则需要根据高斯概率密度函数(什么是高斯分布?高斯分布)进行估计:
然而,上面常见的高斯概率密度函数只是针对一维的参数X,对于大多数情况,输入参数会是多维的,多元高斯概率密度函数怎么求解呢?
可以参考这篇文章:多元正态分布的概率密度函数。
于是,我们得到针对二元变量的概率密度函数求解为:
重点说明下,上面的![]() 参数,是多元变量间的相关性参数,设定值应该小于1。
参数,是多元变量间的相关性参数,设定值应该小于1。
二元变量相关系数求法:

解决问题(python,numpy库支持):
#-*-encoding:utf-8-*-
import numpy
import math
def importdata(filename = 'dataset1.txt') :
'''
导入训练集
'''
f = open(filename,'r')
dataset = []
arr = []
for item in f :
vars = item.split()
dataset.append([float(vars[0]), float(vars[1]), vars[2].upper()])
return dataset
def getParameters(dataset) :
'''
从训练集分别获取不同类别下的期望、方差、标准差、类别的先验概率以及变量间相关系数
'''
class1 = []
class2 = []
class_sum = []
for item in dataset :
class_sum.append([item[0],item[1]])
if item[-1] == 'F' :
class1.append([item[0],item[1]])
if item[-1] == 'M' :
class2.append([item[0],item[1]])
class1 = numpy.array(class1)
class2 = numpy.array(class2)
class_total = numpy.array(class_sum)
mean1 = numpy.mean(class1,axis=0)
variance1 = numpy.var(class1,axis=0)
stand_deviation1 = numpy.std(class1,axis=0)
mean2 = numpy.mean(class2,axis=0)
variance2 = numpy.var(class2,axis=0)
stand_deviation2 = numpy.std(class2,axis=0)
class_total = (len(class1) + len(class2)) * 1.0
mean = numpy.mean(class_sum, axis=0)
stand_deviation = numpy.std(class_sum, axis=0)
new_arr = [ ((item[0] - mean[0]) * (item[1] - mean[1]) / stand_deviation[0] / stand_deviation[1]) for item in dataset]
coefficient = numpy.mean(new_arr)
return (mean1,mean2),(variance1,variance2),(stand_deviation1, stand_deviation2),(len(class1)/class_total,len(class2)/class_total),coefficient
def GaussianFunc(mean, variance, stand_deviation, coefficient) :
'''
根据指定参数(期望、方差、标准差、多元向量间的相关性)生成高斯函数
多元变量的高斯函数
'''
def func(X) :
X = [X[0] - mean[0], X[1] - mean[1]]
B = [[variance[0], coefficient * stand_deviation[0] * stand_deviation[1]],[coefficient * stand_deviation[0] * stand_deviation[1], variance[1]]]
inv_B = numpy.linalg.inv(B)
A = inv_B
B_val = (1.0 - coefficient**2) * variance[0] * variance[1]
tmp1 = 2*math.pi * (B_val ** 0.5)
X = numpy.array([X])
tmp2 = (-0.5) * numpy.dot(numpy.dot(X, A), X.T)
res = 1.0 / tmp1 * (math.e ** tmp2)
return res
return func
def f(X, funcs, class_ps, index) :
'''
贝叶斯概率计算函数
'''
tmp1 = funcs[index](X) * class_ps[index]
tmp2 = funcs[0](X) * class_ps[0] + funcs[1](X) * class_ps[1]
return tmp1 / tmp2
def classify(X,funcs,class_ps,labels) :
'''
基于最小错误率的贝叶斯判别分类。对于二类分类问题,简化了。
'''
res1 = f(X,funcs,class_ps,0)
res2 = f(X,funcs,class_ps,1)
if res1 > res2 :
return labels[0]
else :
return labels[1]
def test(dataset, funcs,class_ps,labels) :
'''
测试
'''
positive0 = 0
positive1 = 0
F = [item for item in dataset if item[-1] == 'F']
len_F = len(F)
len_M = len(dataset) - len_F
for item in dataset :
res = classify([item[0],item[1]], funcs, class_ps,labels)
if res == item[-1] and res == 'F' :
positive0 += 1
if res == item[-1] and res == 'M' :
positive1 += 1
print 'F', positive0 * 1.0 / len_F
print 'M', positive1 * 1.0 / len_M
if __name__ == '__main__' :
dataset = importdata()
(mean1,mean2),(variance1,variance2),(stand_deviation1, stand_deviation2), (class1_p, class2_p), coefficient = getParameters(dataset)
func1 = GaussianFunc(mean1, variance1, stand_deviation1,coefficient)
func2 = GaussianFunc(mean2, variance2, stand_deviation2,coefficient)
#print func1([160,45])
#print func1([170,50])
#print func1([175,50])
#print func1([190,20])
funcs = []
funcs.append(func1)
funcs.append(func2)
class_ps = []
class_ps.append(class1_p)
class_ps.append(class2_p)
classs = [class_ps]
'''
手工指定先验概率
'''
classs.append([0.5,0.5])
classs.append([0.4,0.6])
classs.append([0.3,0.7])
classs.append([0.2,0.8])
labels = ['F', 'M']
for class_ps in classs :
print '-' * 24
print class_ps
print '-'*10,'dataset1','-'*10
testset0 = importdata('dataset1.txt')
test(testset0, funcs, class_ps, labels)
print '-'*10,'dataset2','-'*10
testset1 = importdata('dataset2.txt')
test(testset1, funcs, class_ps, labels)
print '-'*10,'dataset3','-'*10
testset2 = importdata('dataset3.txt')
test(testset2, funcs, class_ps, labels)
实验结果(不同先验概率下的,对dataset1、2、3的测试结果判别正确率,先验概率顺序:F(女)、M(男)):
------------------------
[0.23780487804878048, 0.7621951219512195]
---------- dataset1 ----------
Total 0.92987804878
F 0.807692307692
M 0.968
---------- dataset2 ----------
Total 0.879032258065
F 0.8
M 0.916666666667
---------- dataset3 ----------
Total 0.833333333333
F 0.5625
M 0.891891891892
------------------------
[0.5, 0.5]
---------- dataset1 ----------
Total 0.911585365854
F 0.884615384615
M 0.92
---------- dataset2 ----------
Total 0.862903225806
F 0.85
M 0.869047619048
---------- dataset3 ----------
Total 0.844444444444
F 0.6875
M 0.878378378378
------------------------
[0.4, 0.6]
---------- dataset1 ----------
Total 0.926829268293
F 0.871794871795
M 0.944
---------- dataset2 ----------
Total 0.879032258065
F 0.825
M 0.904761904762
---------- dataset3 ----------
Total 0.855555555556
F 0.6875
M 0.891891891892
------------------------
[0.3, 0.7]
---------- dataset1 ----------
Total 0.92987804878
F 0.846153846154
M 0.956
---------- dataset2 ----------
Total 0.887096774194
F 0.825
M 0.916666666667
---------- dataset3 ----------
Total 0.855555555556
F 0.6875
M 0.891891891892
------------------------
[0.2, 0.8]
---------- dataset1 ----------
Total 0.932926829268
F 0.807692307692
M 0.972
---------- dataset2 ----------
Total 0.862903225806
F 0.725
M 0.928571428571
---------- dataset3 ----------
Total 0.822222222222
F 0.5
M 0.891891891892