面试题_二分查找及其变形
二分查找常用来查找指定有序集合中元素的位置，思路和代码都比较简单，所以大家都很熟练。二分查找貌似很多公司在面试或笔试的时候都会多少涉及到，经常会让你在纸上直接写代码，所以平常只知道原理而从来不自己写的人，可能不会太快写出来，或是代码有点小漏洞，所以经常敲敲常见的数据结构和代码还是很必要的。
很多问题，只要涉及到有序的数据结构，就可以往二分查找的思路上靠。 下面的代码，可能不是很完善，仅供参考。
经典二分查找的代码，在有序数组里面查找是否存在某个元素，如果存在，则返回相应元素所在索引号：
{
assert(arr!=NULL&&length>0);
int low=0,high=length,mid;
while(low<=high)
{
mid=(low+high)/2;
if(arr[mid]==key) return mid;
else
{
if(arr[mid]>key) high=mid-1;
else low=mid+1;
}
}
return-1;
}
变形1：
问题来了：在循环有序数组中查找指定元素，也就是说在类似这样的{12,16,18,20,41,100,1,4,6,9}数组中查找指定的元素。
分析一下，这里所说的循环有序数组，就是把一个有序数组从某个（未知）位置处截为两段，把前一段放到后一段的后面（数组里的元素还是有序的，只不过最小值不一定是数组的第一个元素，而可能是其中的任何一项，从它开始逐项递增，到数组的最后一个元素时再回到第一个元素）。
显然传统的二分法已经无法直接使用了，但考虑一下，如果已经知道分界点位置，那问题就简单多了，只要先判断一下待查元素是在分界点的左侧还是右侧，然后直接对那一侧的半个数组使用二分查找。
那么重点就是判定待测元素在分界点的左侧还是右侧的问题了，可以发现每次取mid后，就会形成两种情况的子序列。一种情况是类似{4,6,9}，他是一个正常有序的子集合，另一种情况是类似{12,16,18,20,41,100,1}的与源问题类似结构的相对复杂的子集合。显然第一种情况是简单的，那么判定待测元素在分界点的简单一侧会比较容易。
第一种情况（arr[mid]>=arr[low]）：当key<=arr[mid]&&key>=arr[low]时，待测元素肯定会在mid的左侧；其他情形则会在mid的右侧。
第二种情况（arr[mid]<arr[low]）：当key<=arr[low]&&key>=arr[mid]时，待测元素肯定会在mid的右侧，其他情形则会在mid的左侧。
上面两个子条件的选择比较重要。
最后给出代码：
int find ( int * arr, int low , int high, int key)
{
int mid ;
while(low<=high)
{
mid = (low+high)/2;
if (arr[mid] == key ) return mid;
if(arr[mid]>=arr[low])
{
if(key<=arr[mid]&&key>=arr[low]) high = mid -1;
else low = mid +1;
}
else
{
if(key<=arr[high]&&key>=arr[mid]) low = mid + 1;
else high = mid -1;
}
}
return -1;
}
变形2：假如集合中的元素有重复，要找到key首次出现的位置。
int find(int * arr , int length, int key){ int low = 0,high = length-1,mid; while(low <= high){ mid = (low + high)/2; if (arr[mid] < key){ low = mid + 1; }else if(arr[mid] > key){ high = mid - 1; }else{ if (mid == 0) return mid; if (mid >= 1 && arr[mid-1] != key) return mid; else high = mid - 1; } } return -1; }
变形3：在一个有序的数组里，查找不小于key的最小的数的索引，如果key值存在，则返回key第一次出现的位置，如果不存在则返回-1。（类似的查找比key小的最大的数）
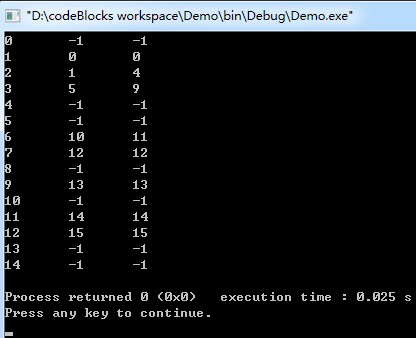
#include<iostream> using namespace std; int find(int * arr, int low, int high, int key){ if(arr[low] >= key) return low; if (low > high) return -1; int mid = (low + high) / 2; if (arr[mid] < key) return find(arr,mid+1,high,key); else if(arr[mid] >= key){ if(mid >= low && arr[mid-1]>=key) return find(arr,low, mid-1, key); return mid; } } int main(){ int arr[] = {1,3,3,3,3,3,6,6,7,9,11,12}; int length = sizeof(arr) / sizeof(int); cout<<"KEY"<<"\t"<<"索引"<<"\t"<<"对应值"<<endl; for(int i=0;i<15;i++){ int idx = find(arr,0,length-1,i); if (idx >= 0) cout<<i<<"\t"<<idx<<"\t"<<arr[idx]<<endl; else cout<<i<<"\t"<<idx<<"\t"<<"None"<<endl; } return 0; }
变形4：在一个有序的数组里，数据里面元素可能有重复的，查找指定key所在的索引范围。
例如：int arr[] = {1,2,2,2,2,3,3,3,3,3,6,6,7,9,11,12}; 查找3的话，应该返回（5,9）
分析一下： 一个思路是，先随意找到一个key所在的索引i，然后从i的左右两侧查找，直到左右两侧遇到不等于key的值为止，然后返回两边的索引号。
但是，这样存在一个问题，考虑一下如果一个数组是{1,2,3,3,3,3,3,3,3,4}，这样按照上面的想法就很扯淡了，因为与key相等的值太多了，比较代价太大。
于是可以考虑，用两次二分查找，找两个边界，这里我们可以使用变形3中所写好的find函数，我们去找比key+1大的最小的索引right，以及比key大的最小值得索引left。
返回结果，即为<left,right-1>
这里有个问题必须指出，在变形3我们写的函数中，如果key存在则返回key第一次出现的位置。
int find(int * arr, int low, int high, int key){ if(arr[low] >= key) return low; if (low > high) return -1; int mid = (low + high) / 2; if (arr[mid] < key) return find(arr,mid+1,high,key); else if(arr[mid] >= key){ if(mid >= low && arr[mid-1]>=key) return find(arr,low, mid-1, key); return mid; } } pair<int,int> findRange(int * arr, int length, int key){ pair<int,int> res(-1,-1); int l = find(arr, 0,length-1, key); if(l<0 || arr[l] != key) return res; res.first = l; int r = find(arr, 0, length-1, key+1); if(r-1<0 || arr[r-1] != key) return res; res.second = r-1; return res; } int main(){ int arr[] = {1,2,2,2,2,3,3,3,3,3,6,6,7,9,11,12}; int length = sizeof(arr) / sizeof(int); for (int i=0;i<15;i++){ pair<int,int> res = findRange(arr, length,i); cout<<i<<"\t"<<res.first<<"\t"<<res.second<<endl; } return 0; }
