二分图算法
1 判定: 采用 bfs 搜索染色

#include<bits/stdc++.h> using namespace std; #define LOACL freopen("in","r",stdin);\ freopen("out","w",stdout); const int inf = 987654321; const int sz = 1e6 + 5; const int mod = 1e9 + 7; const int sqrtn = 300; #define add(u,v,w) (e[++tot]=(edge){v,head[u],1},head[u]=tot;) #define f(i,l,r) for(int i=l;i<=r;++i) #define g(i,l,r) for(int i=l;i>=r;--i) #define CLR(arr,val) memset(arr,val,sizeof(arr)) typedef long long ll; int t ,n,m,u,v; #define MAXN 10001 bool graph[MAXN][MAXN]; int state[MAXN]; bool bfs(int s ) { queue <int >q ; q.push(s); state[s]=1; while(!q.empty()) { int t = q.front(); q.pop(); f(i,1,n) { if(t!=i && graph[t][i]) { if(state[i]==0) { q.push(i); state[i] = -state[t]; } if(state[i] == state[t]) return false; } } } return true; } bool check(int n) { bool flag =false; f(i,1,n) { if(state[i]==0) { bool reasult= bfs(i); if(reasult ==false) return false; } } return true; } int main() { LOACL cin>>t; while(t--) { CLR(graph,0); CLR(state,0); cin>>n>>m; f(i,1,m) { cin>>u>>v; graph[u][v]=1; graph[v][u]=1; } if(check(n)) cout<<"Correct"<<endl; else cout<<"Wrong"<<endl; } return 0; }
2.最大匹配之匈牙利算法
图G=(V,E)。在上一回中我们已经知道这个图可以被染成黑白两色。不妨将所有表示女性的节点记为点集A,表示男性的节点记为点集B。则有A∪B=V。由问题可知所有边e的两个端点分别属于AB两个集合。则可以表示成如下的图:
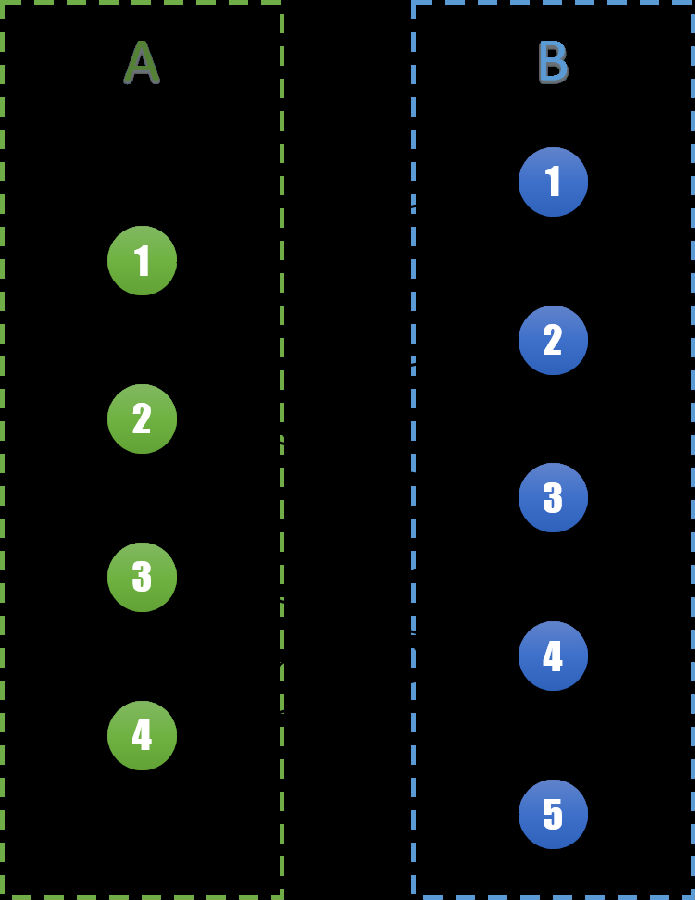
同样的,我们将所有的边分为两个集合。集合S和集合M,同样有S∪M=E。边集S表示在这一轮相亲会中将要进行的相亲,边集M表示在不在这一次进行。对于任意边(u,v) ∈ S,我们称u和v为一组匹配,它们之间相互匹配。在图G,我们将边集S用实线表示,边集M用虚线表示。得到下图:
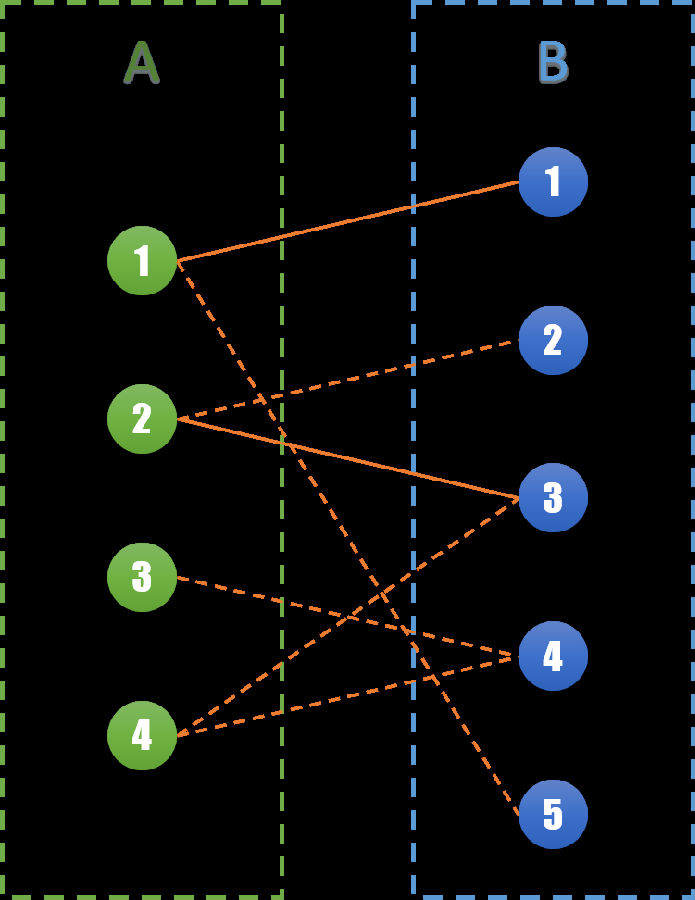
则原问题转化为,最多能选择多少条边到集合S,使得S集合中任何两条边不相邻(即有共同的顶点)。显然的,|S|<=Min{|A|, |B|}。
那么能不能找到一个算法,使得能够很容易计算出尽可能多的边能够放入集合S?我们不妨来看一个例子:

对于已经匹配的点我们先不考虑,我们从未匹配的点来做。这里我们选择A集合中尚未匹配的点(A3和A4)考虑:
对于A3点,我们可以发现A3与B4右边相连,且都未匹配。则直接将(A3,B4)边加入集合S即可。
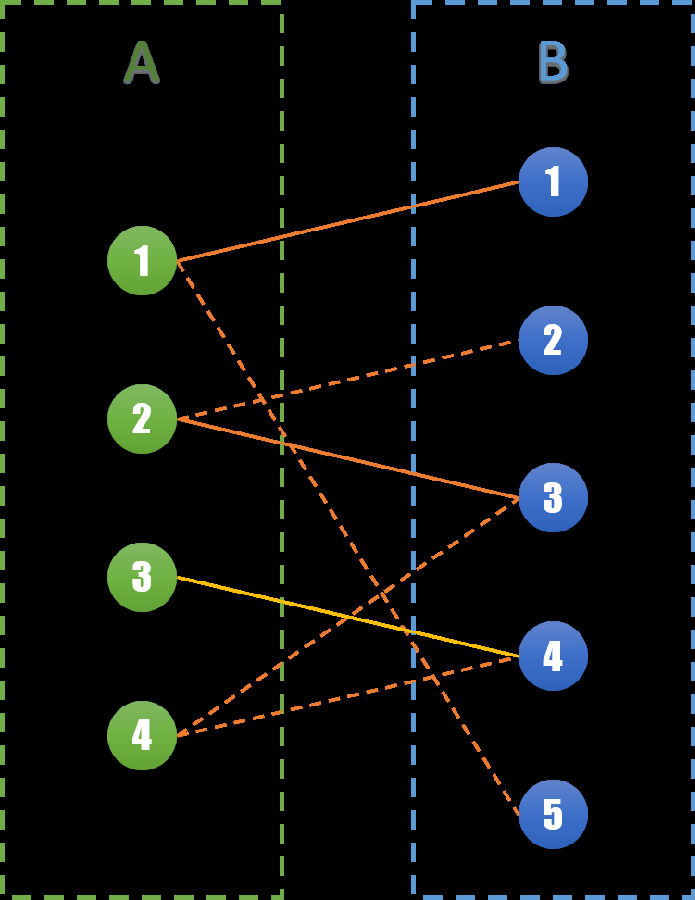
对于A4点,我们发现和A4相连的B3,B4点都已经匹配了。但是再观察可以发现,如果我们将A2和B2相连,则可以将B3点空出来。那么就可以同时将(A2,B2),(A4,B3)相连。将原来的一个匹配变成了两个匹配。
让我们来仔细看看这一步:我们将这次变换中相关联的边标记出来,如下图所示紫色的3条边(A2,B2),(A2,B3),(A4,B3)。
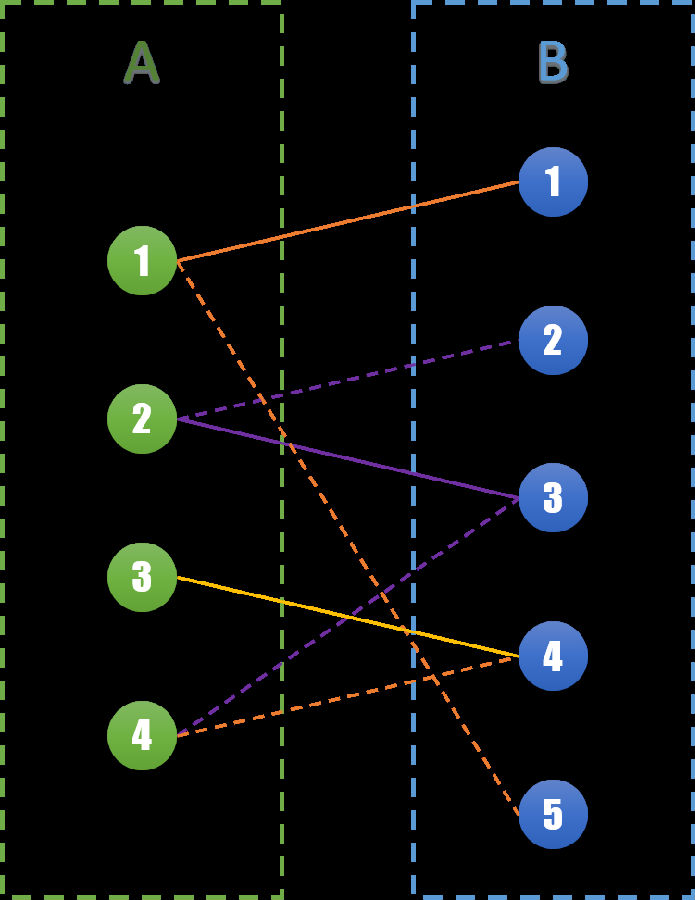
这三条边构成了一条路径,可以发现这条路径有个非常特殊的性质。虚线和实线相互交错,并且起点和终点都是尚未匹配的点,且属于两个不同的集合。我们称这样的路径为交错路径。
再进一步分析,对于任意一条交错路径,虚线的数量一定比实线的数量多1。我们将虚线和实线交换一下,就变成了下面的图:
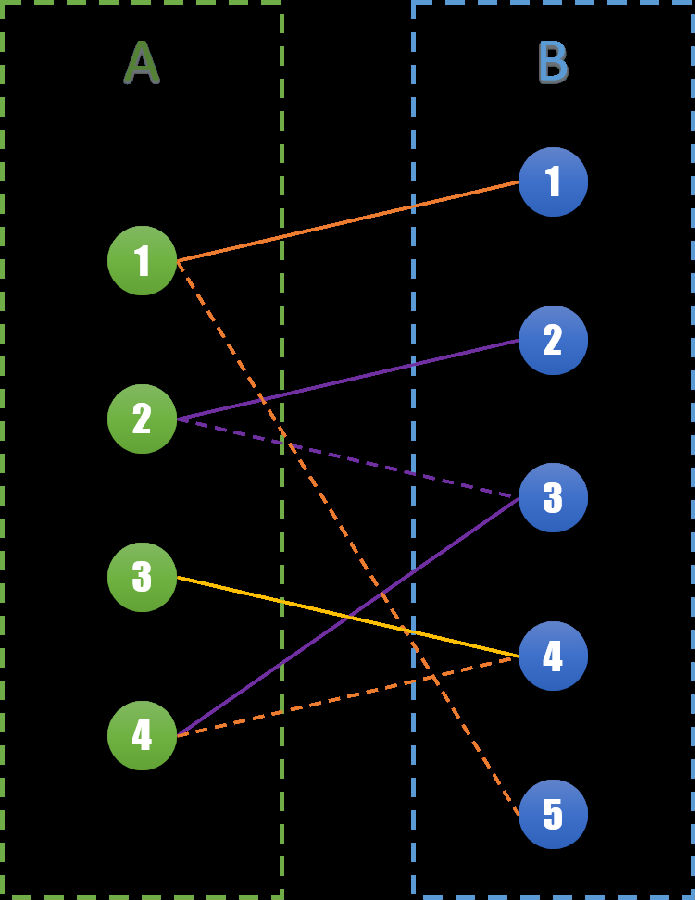
在原来1个匹配的基础上,我们得到了2个新的匹配,S集合边的数量也增加了1。并且原来在已经匹配的点仍然是已经匹配的状态。
再回头看看A3点匹配时的情况:对于(A3,B4)这一条路径,同样满足了交错路径的性质。
至此我们得到了一个找新匹配的有效算法:
选取一个未匹配的点,查找是否存在一条以它为起点的交错路径。若存在,将该交错路径的边虚实交换。否则在当前的情况下,该点找不到可以匹配的点。
又有对于已经匹配的点,该算法并不会改变一个点的匹配状态。所以当我们对所有未匹配的点都计算过后,仍然没有交错路径,则不可能找到更多的匹配。此时S集合中的边数即为最大边数,我们称为最大匹配数。

#include<bits/stdc++.h> using namespace std; #define LOACL freopen("in","r",stdin);\ freopen("out","w",stdout); const int inf = 987654321; const int sz = 1e6 + 5; const int mod = 1e9 + 7; const int sqrtn = 300; #define add(u,v,w) (e[++tot]=(edge){v,head[u],1},head[u]=tot;) #define f(i,l,r) for(int i=l;i<=r;++i) #define g(i,l,r) for(int i=l;i>=r;--i) #define CLR(arr,val) memset(arr,val,sizeof(arr)) typedef long long ll; int n,m,u,v; vector<int> G[sz]; int b[sz]; bool vis[sz]; int ans; bool dfs(int s ) { f(i,0,G[s].size()-1) { int v = G[s][i]; if(!vis[v]) { vis[v]=true; if(b[v]==0 || dfs(b[v])) { b[v]=s; return true; } } } return false; } int main() { LOACL cin>>n>>m; f(i,1,m) { cin>>u>>v; G[u].push_back(v); G[v].push_back(u); } CLR(b,0); f(i,1,n) { CLR(vis,false); if(dfs(i))ans++; } cout<<ans/2<<endl; return 0; }
3.图最小点覆盖 ========>二分图最大匹配
4.最大独立集 =========> n - 二分图最大匹配



 浙公网安备 33010602011771号
浙公网安备 33010602011771号