博弈论 Nim,sg

博弈论

首先，定义一下 状态Position P 先手必败 N x先手必胜

操作方法： 反向转移

 相同状态 不同位置 的一对 相当于无

对于ICG游戏，我们可以将游戏中每一个可能发生的局面表示为一个点。并且若存在局面i和局面j，且j是i的后继局面(即局面i可以转化为局面j)，我们用一条有向边，从i出发到j，连接表示局面i和局面j的点。则整个游戏可以表示成为一个有向无环图：

根据ICG游戏的定义我们知道，任意一个无法继续进行下去的局面为终结局面，即P局面(先手必败)。在上图中我们可以标记所有出度为0的点为P点。接着根据ICG游戏的两条性质，我们可以逆推出所有点为P局面还是N局面：

对于一个游戏可能发生的局面x，我们如下定义它的sg值：
(1)若当前局面x为终结局面，则sg值为0。
(2)若当前局面x非终结局面，其sg值为：sg(x) = mex{sg(y) | y是x的后继局面}。
mex{a[i]}表示a中未出现的最小非负整数。举个例子来说：
mex{0, 1, 2} = 3, mex{1, 2}=0, mex{0,1,3}=2

我们将上图用sg函数表示后，得到：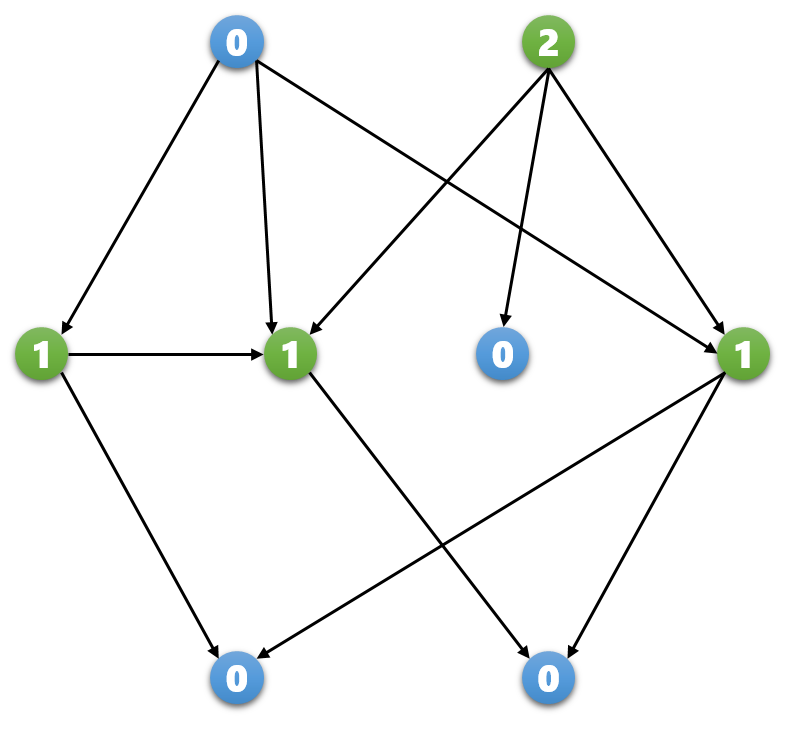

可以发现，若一个局面x为P局面，则有sg(x)=0；否则sg(x)>0。同样sg值也满足N、P之间的转换关系：
若一个局面x，其sg(x)>0，则一定存在一个后续局面y，sg(y)=0。
若一个局面x，其sg(x)=0，则x的所有后续局面y，sg(y)>0。

由上面的推论，我们可以知道用N、P-Position可以描述的游戏用sg同样可以描述。并且在sg函数中还有一个非常好用的定理，叫做sg定理：
对于多个单一游戏，X=x[1..n]，每一次我们只能改变其中一个单一游戏的局面。则其总局面的sg值等于这些单一游戏的sg值异或和。

 

 

 

 

 

 

 

#include<bits/stdc++.h>
using namespace std;
#define LOACL  freopen("in","r",stdin);\
            freopen("out","w",stdout); 

const int  inf = 987654321;
const int sz = 1e6 + 5;
const int mod = 1e9 + 7;
const int sqrtn = 300; 

#define add(u,v,w) (e[++tot]=(edge){v,head[u],1},head[u]=tot;) 
#define f(i,l,r) for(int i=l;i<=r;++i)
#define g(i,l,r) for(int i=l;i>=r;--i)
#define CLR(arr,val) memset(arr,val,sizeof(arr)) 
typedef long long ll; 
int n,x,s;
int main()
{
    LOACL
    cin>>n;
    f(i,1,n) 
    {
        cin>>x;     
        s^=x;
    } 
    if(s)cout<<"Alice"<<endl;
    else cout<<"Bob"<<endl;
    return 0;
}

#include<bits/stdc++.h>
using namespace std;
#define LOACL  freopen("in","r",stdin);\
            freopen("out","w",stdout); 

const int  inf = 987654321;
const int sz = 1e6 + 5;
const int mod = 1e9 + 7;
const int sqrtn = 300; 

#define add(u,v,w) (e[++tot]=(edge){v,head[u],1},head[u]=tot;) 
#define f(i,l,r) for(int i=l;i<=r;++i)
#define g(i,l,r) for(int i=l;i>=r;--i)
#define CLR(arr,val) memset(arr,val,sizeof(arr)) 
typedef long long ll; 

int main()
{
    LOACL
     int n ;
     cin>>n;
     getchar(); //吃换行
     char c;
     int ans=0;
     f(i,1,n)
     {
         c=getchar();
         if(c=='H')
             ans^=i;
     }
     if(ans)cout<<"Alice"<<endl;
    else cout<<"Bob"<<endl;
    return 0;
}

 #include<bits/stdc++.h>
 using namespace std;
 #define LOACL  freopen("in","r",stdin);\
             freopen("out","w",stdout); 
 
 const int  inf = 987654321;
 const int sz = 1e6 + 5;
 const int mod = 1e9 + 7;
 const int sqrtn = 300; 
 
 #define add(u,v,w) (e[++tot]=(edge){v,head[u],1},head[u]=tot;) 
 #define f(i,l,r) for(int i=l;i<=r;++i)
 #define g(i,l,r) for(int i=l;i>=r;--i)
 #define CLR(arr,val) memset(arr,val,sizeof(arr)) 
 typedef long long ll; 
 
 int main()
 {
     LOACL
    int n ,x,sg=0;
    cin>>n;
    f(i,1,n)
    {
        cin>>x;
        if(((x+x&1)>>1)&1) sg^=x;
        else sg^= (x&1)?x+1:x-1;
    }
    if(sg)cout<<"Alice"<<endl;
    else cout<<"Bob"<<endl;
     return 0;
    
 }