聚类算法学习总结

1.1 聚类的定义

聚类(Clustering)是按照某个特定标准(如距离)把一个数据集分割成不同的类或簇，使得同一个簇内的数据对象的相似性尽可能大，同时不在同一个簇中的数据对象的差异性也尽可能地大。也即聚类后同一类的数据尽可能聚集到一起，不同类数据尽量分离。

1.2 聚类和分类的区别

• 聚类(Clustering)：是指把相似的数据划分到一起，具体划分的时候并不关心这一类的标签，目标就是把相似的数据聚合到一起，聚类是一种无监督学习(Unsupervised Learning)方法。
• 分类(Classification)：是把不同的数据划分开，其过程是通过训练数据集获得一个分类器，再通过分类器去预测未知数据，分类是一种监督学习(Supervised Learning)方法。

1.3 聚类的一般过程

1. 数据准备：特征标准化和降维
2. 特征选择：从最初的特征中选择最有效的特征，并将其存储在向量中
3. 特征提取：通过对选择的特征进行转换形成新的突出特征
4. 聚类：基于某种距离函数进行相似度度量，获取簇
5. 聚类结果评估：分析聚类结果，如距离误差和(SSE)等

二、数据聚类方法

数据聚类方法主要可以分为划分式聚类方法(Partition-based Methods)、基于密度的聚类方法(Density-based methods)、层次化聚类方法(Hierarchical Methods)等。

 

 

划分式聚类方法需要事先指定簇类的数目或者聚类中心，通过反复迭代，直至最后达到"簇内的点足够近，簇间的点足够远"的目标。经典的划分式聚类方法有k-means及其变体k-means++、bi-kmeans、kernel k-means等。

2.1.2 k-means算法

经典的k-means算法的流程如下：

经典k-means源代码，下左图是原始数据集，通过观察发现大致可以分为4类，所以取�=4，测试数据效果如下右图所示。

 

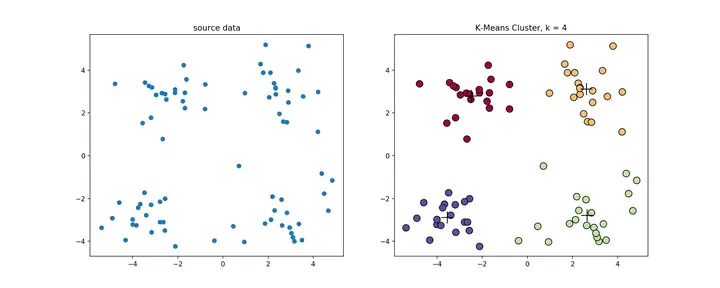
一般来说，经典k-means算法有以下几个特点：

1. 需要提前确定k值
2. 对初始质心点敏感
3. 对异常数据敏感

2.1.2 k-means++算法

k-means++是针对k-means中初始质心点选取的优化算法。该算法的流程和k-means类似，改变的地方只有初始质心的选取，该部分的算法流程如下

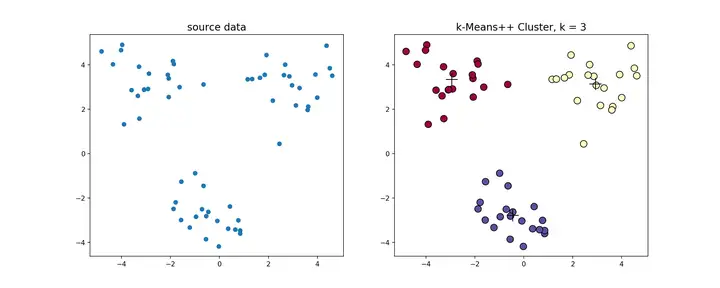
k-means++源代码，使用k-means++对上述数据做聚类处理，得到的结果如下

2.1.3 bi-kmeans算法

一种度量聚类效果的指标是SSE(Sum of Squared Error)，他表示聚类后的簇离该簇的聚类中心的平方和，SSE越小，表示聚类效果越好。 bi-kmeans是针对kmeans算法会陷入局部最优的缺陷进行的改进算法。该算法基于SSE最小化的原理，首先将所有的数据点视为一个簇，然后将该簇一分为二，之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分是否能最大程度的降低SSE的值。

该算法的流程如下：

bi-kmeans算法源代码，利用bi-kmeans算法处理上节中的数据得到的结果如下图所示。

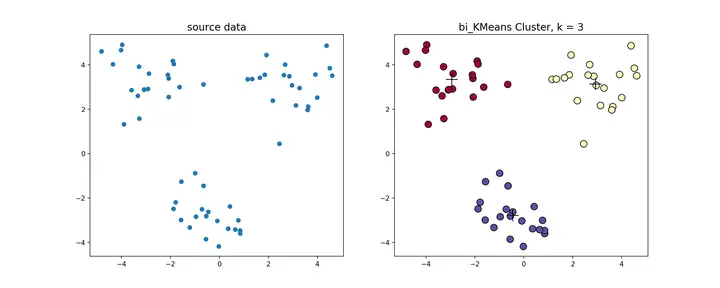
这是一个全局最优的方法，所以每次计算出来的SSE值基本也是一样的（但是还是不排除有部分随机分错的情况），我们和前面的k-means、k-means++比较一下计算出来的SSE值

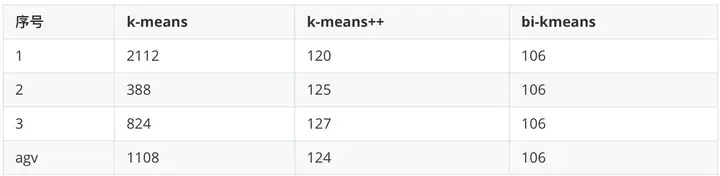
可以看到，k-means每次计算出来的SSE都较大且不太稳定，k-means++计算出来的SSE较稳定并且数值较小，而bi-kmeans 4次计算出来的SSE都一样，并且计算的SSE都较小，说明聚类的效果也最好。

2.2 基于密度的方法

k-means算法对于凸性数据具有良好的效果，能够根据距离来讲数据分为球状类的簇，但对于非凸形状的数据点，就无能为力了，当k-means算法在环形数据的聚类时，我们看看会发生什么情况。

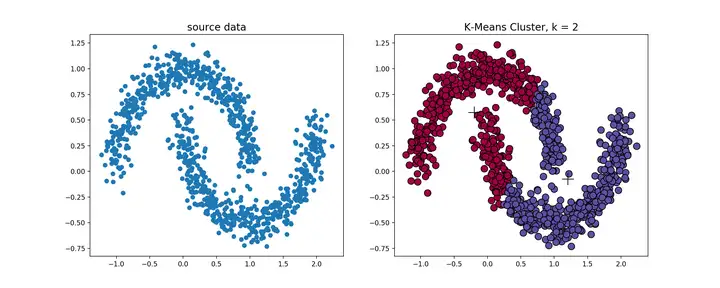
从上图可以看到，kmeans聚类产生了错误的结果，这个时候就需要用到基于密度的聚类方法了，该方法需要定义两个参数m和n，分别表示密度的邻域半径和邻域密度阈值。DBSCAN就是其中的典型。