【实验】粒子群算法的超参数优化
粒子群算法的超参数优化
粒子群算法概述
粒子群优化算法(Particle Swarm Optimization)是由美国的Kennedy和Eberhart 两位博士提出的一种优化算法。这种算法基于Boid模型。Reynolds通过观察自然界中,鸟类聚集飞行的行为,提出了Boid模型。在 Boid中,每个个体是一个 Boid,它们各自均可感知到周围其他Boid 的位置信息。然后,利用该信息来作为决策自身行动的一个依据。最后结合自身状态(一般为位置、速度、方向等),更新自身的位置。
粒子群算法的原理
- 速度更新$$v_{id}{t}+c_1r_1(pbestt_{id}-x_{id}2)+c_2r_2(gbest_dt-x_{id}^t)$$
- 位置更新$$x_{id}{t+1}=x_{id}t+v_{id}^t$$

wine数据集代码运行流程
主要是进行一个分类器的超参数优化;
超参数:
- n_estimators
- learning_rate
- algorithm
前置条件:
MAX_Generation = 5
Population = 5
dimension = 3
v_low = [-5,-0.1,-0.5]
v_high = [5,0.1,0.5]
# [n_estimators, learning_rate, algorithm]:
BOUNDS_LOW = [1, 0.01, 0]
BOUNDS_HIGH = [100, 1.00, 1]
为了方便查看一个五个个体的粒子群迭代五次。
虽然可以一次性展示出来,但是我懒得改代码了,应该改成迭代三次的!!!
初始化数据
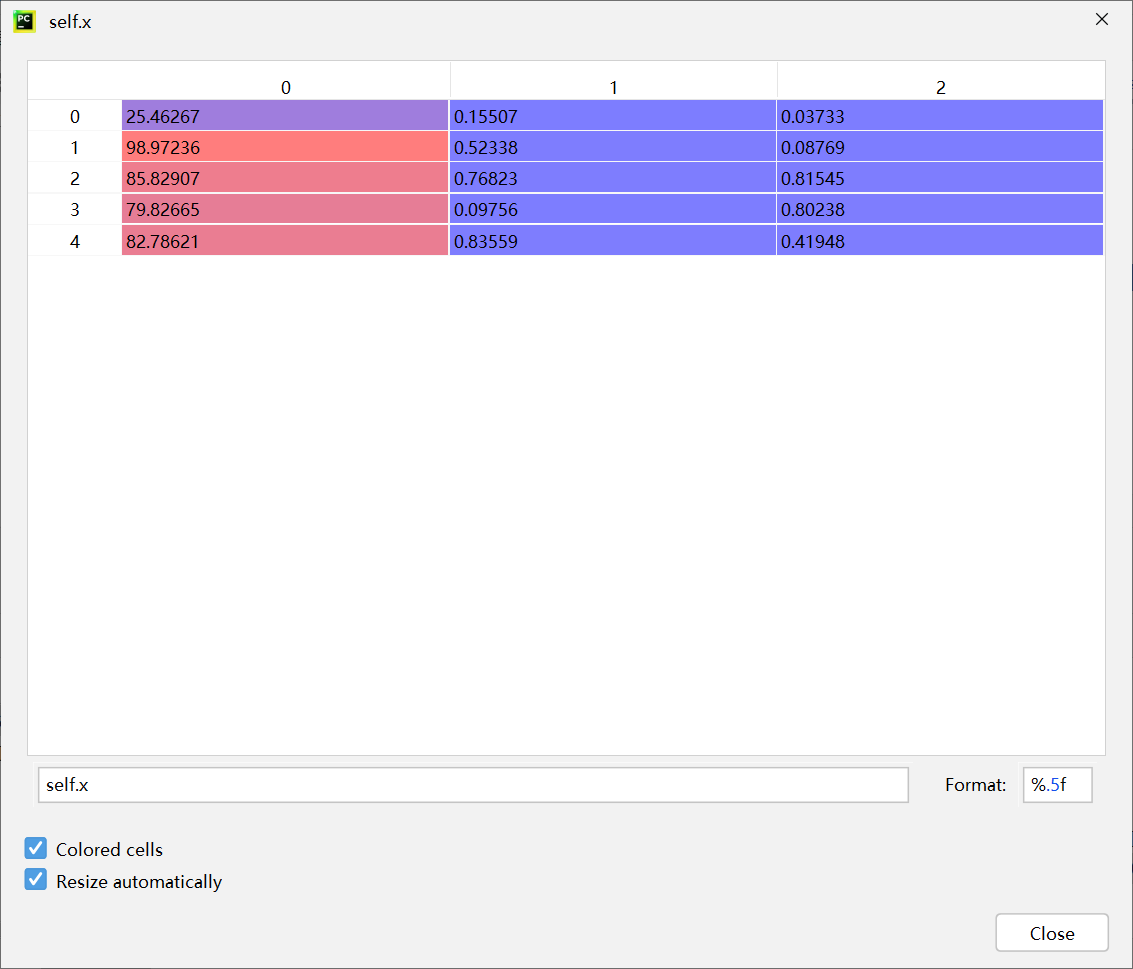
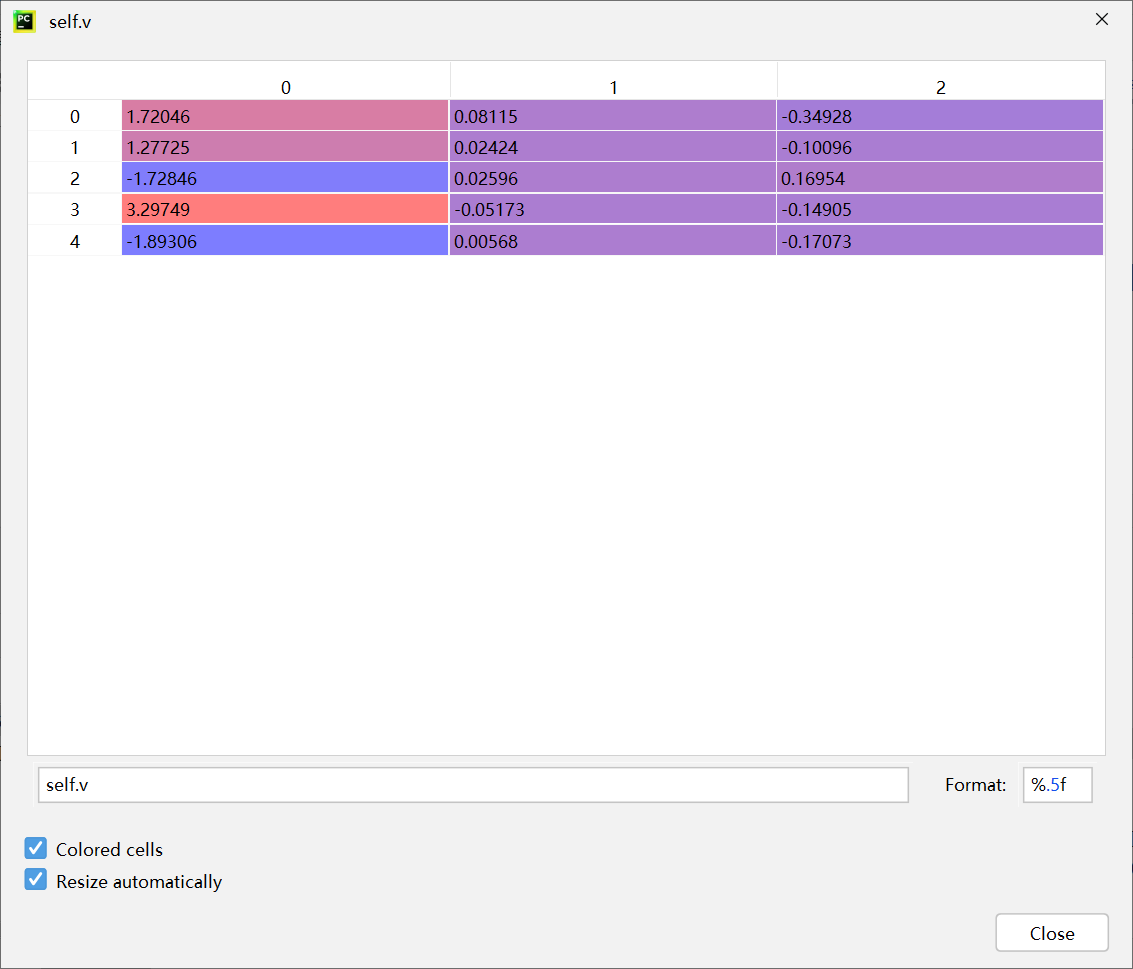
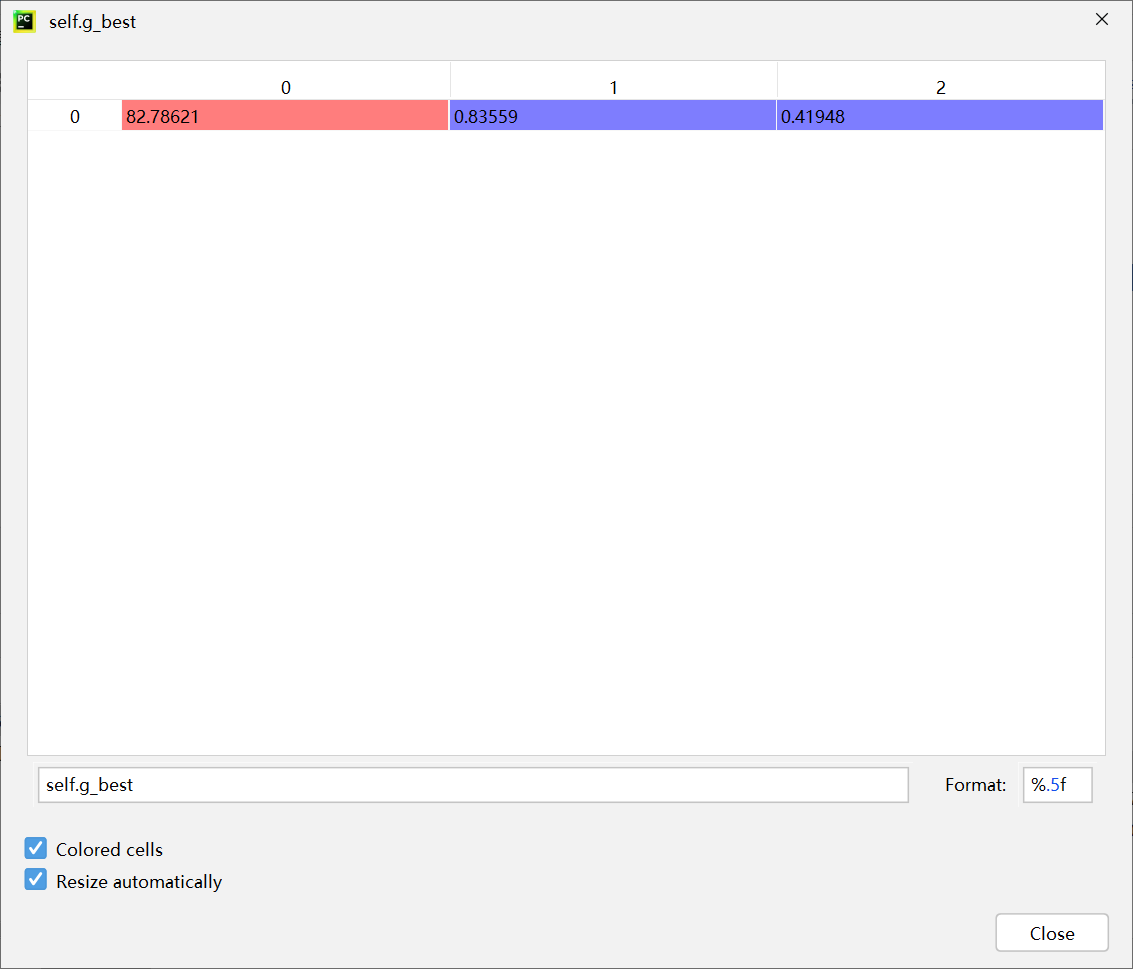
对应g_best(global best individual)的适应度:0.9607936507936508
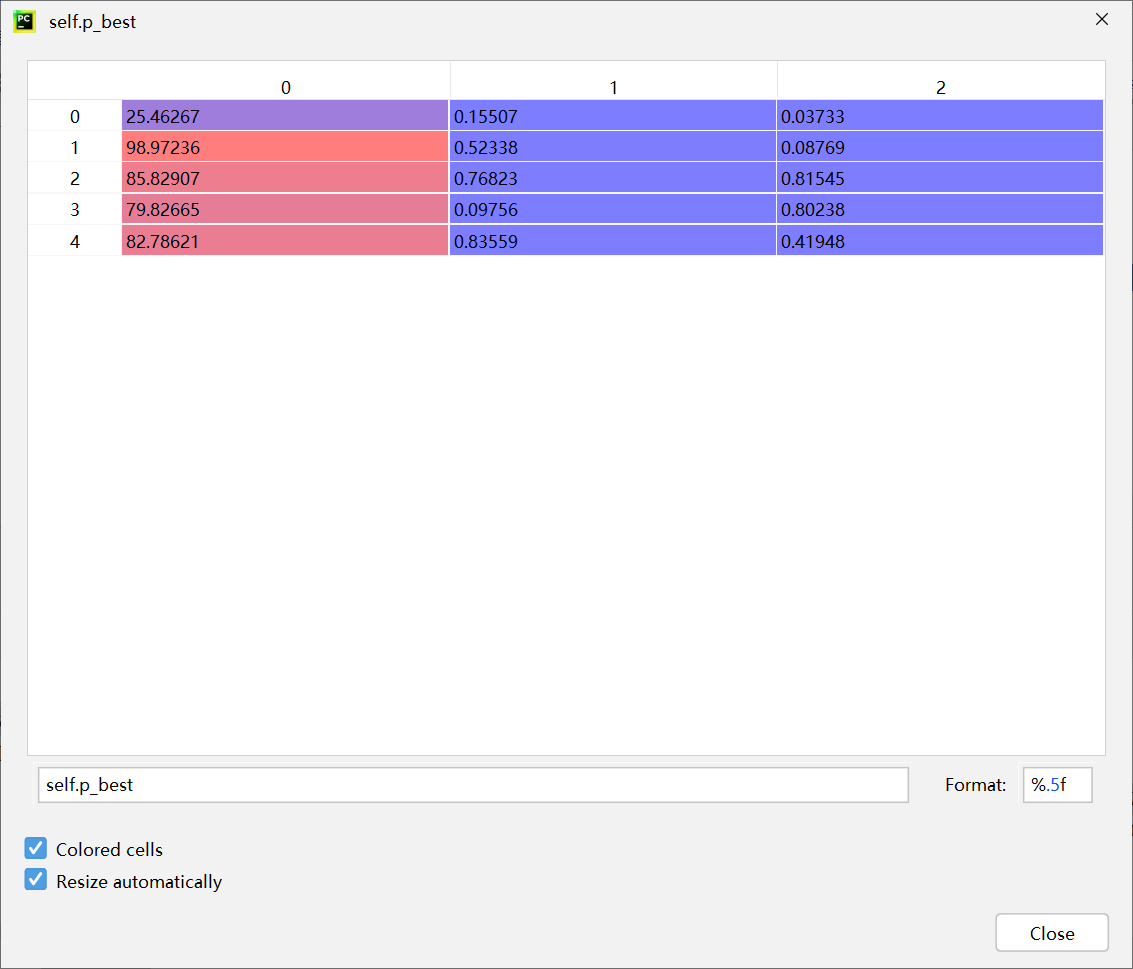
对应上面的p_best(personal best individual)个体适应度
[0.9099999999999999, 0.9606349206349206, 0.943968253968254, 0.9212698412698412, 0.9607936507936508]
第一次迭代
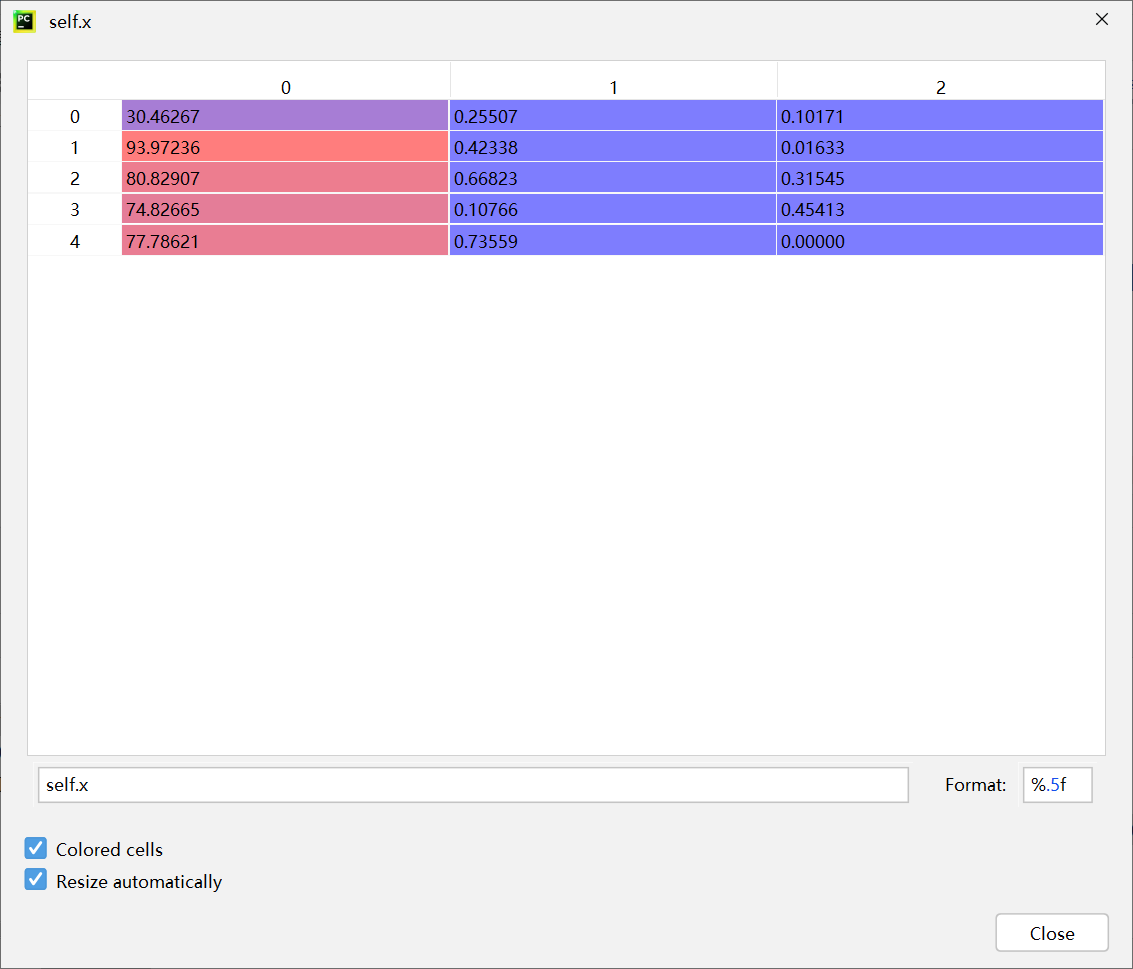


fitness: 0.9663492063492063
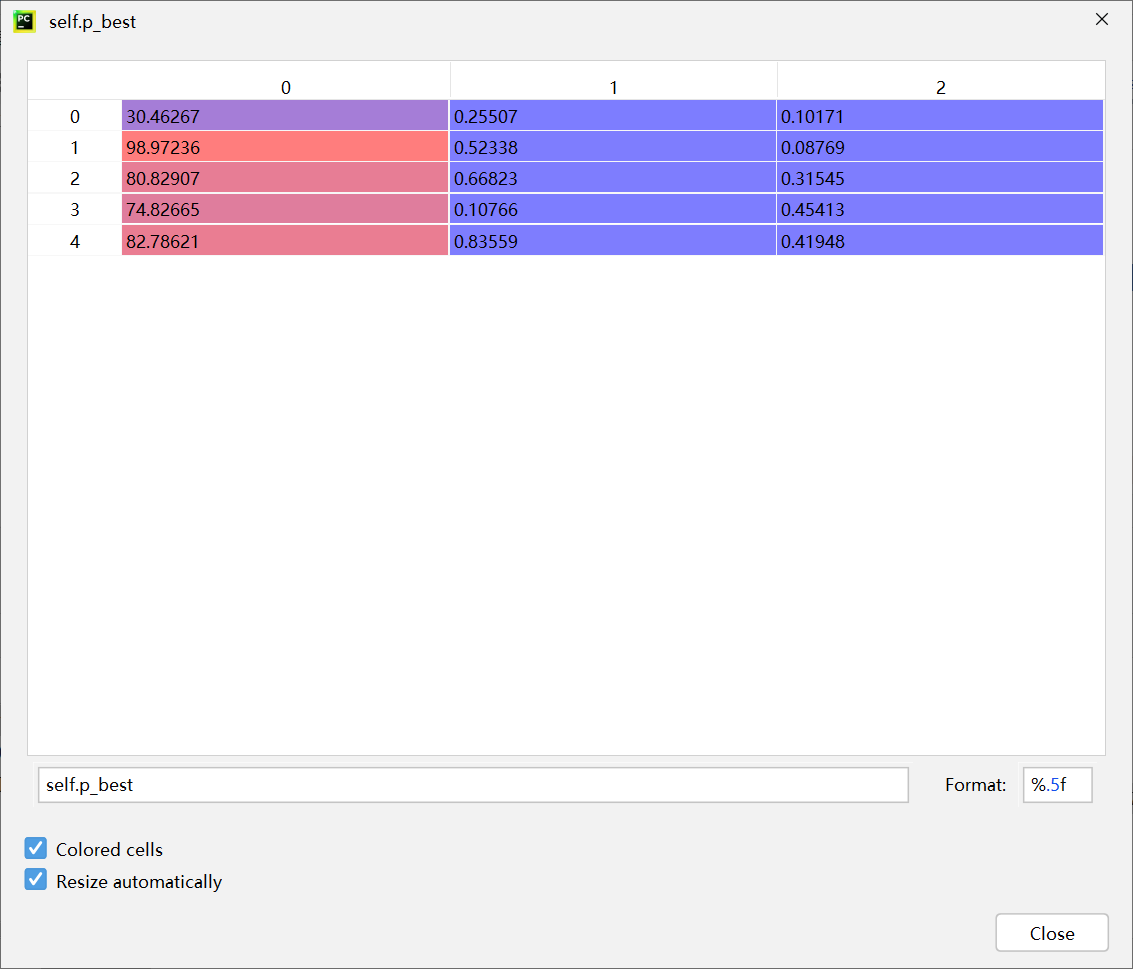
fitness:
[0.9663492063492063, 0.9606349206349206, 0.9607936507936508, 0.9495238095238093, 0.9607936507936508]
第二次迭代
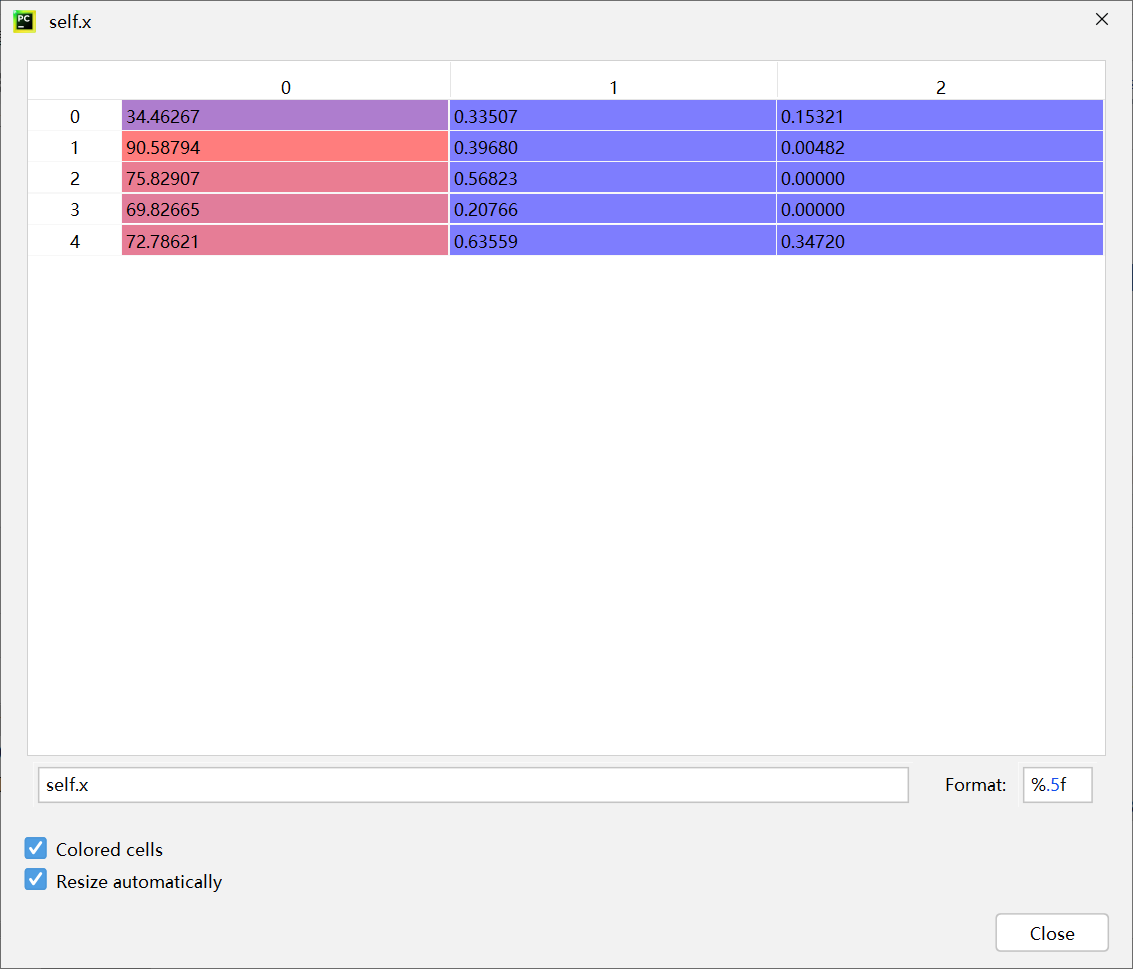
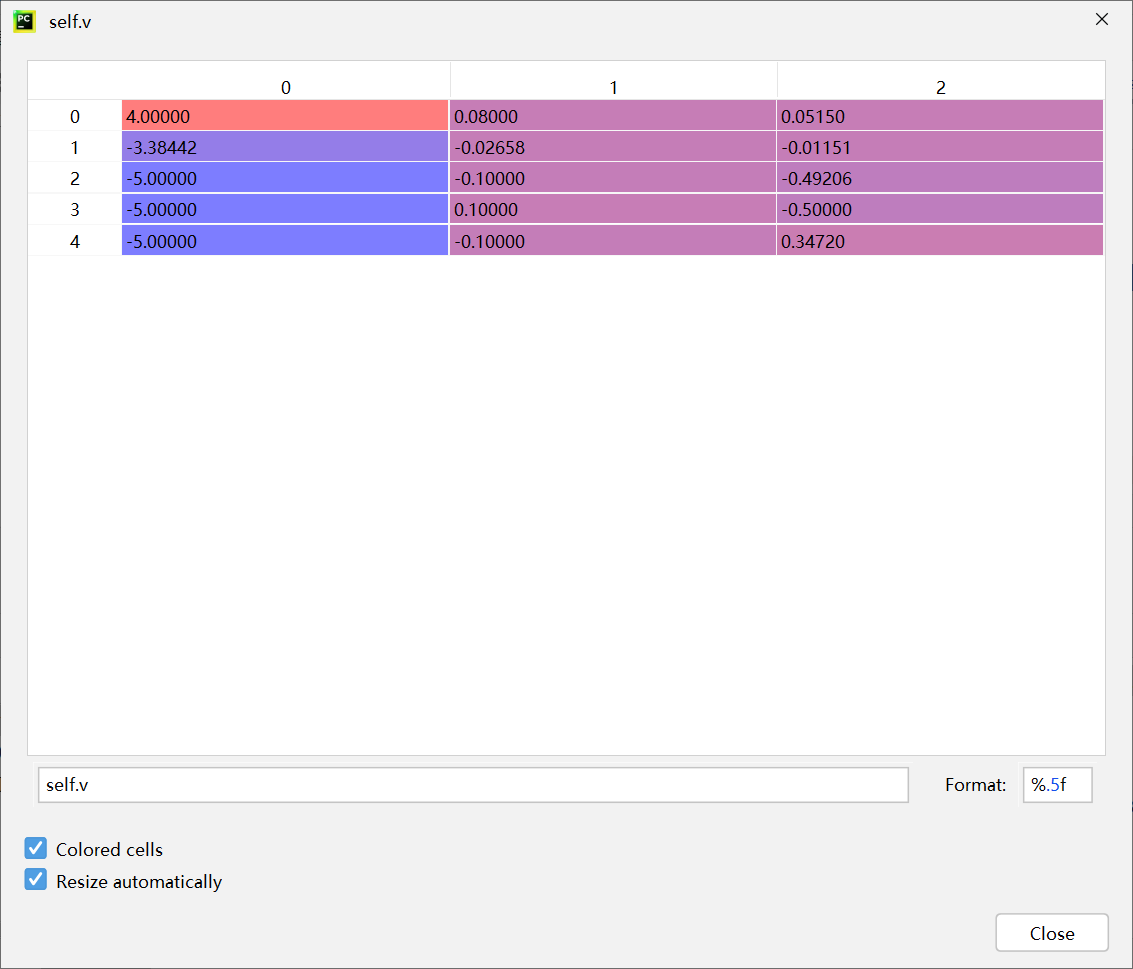
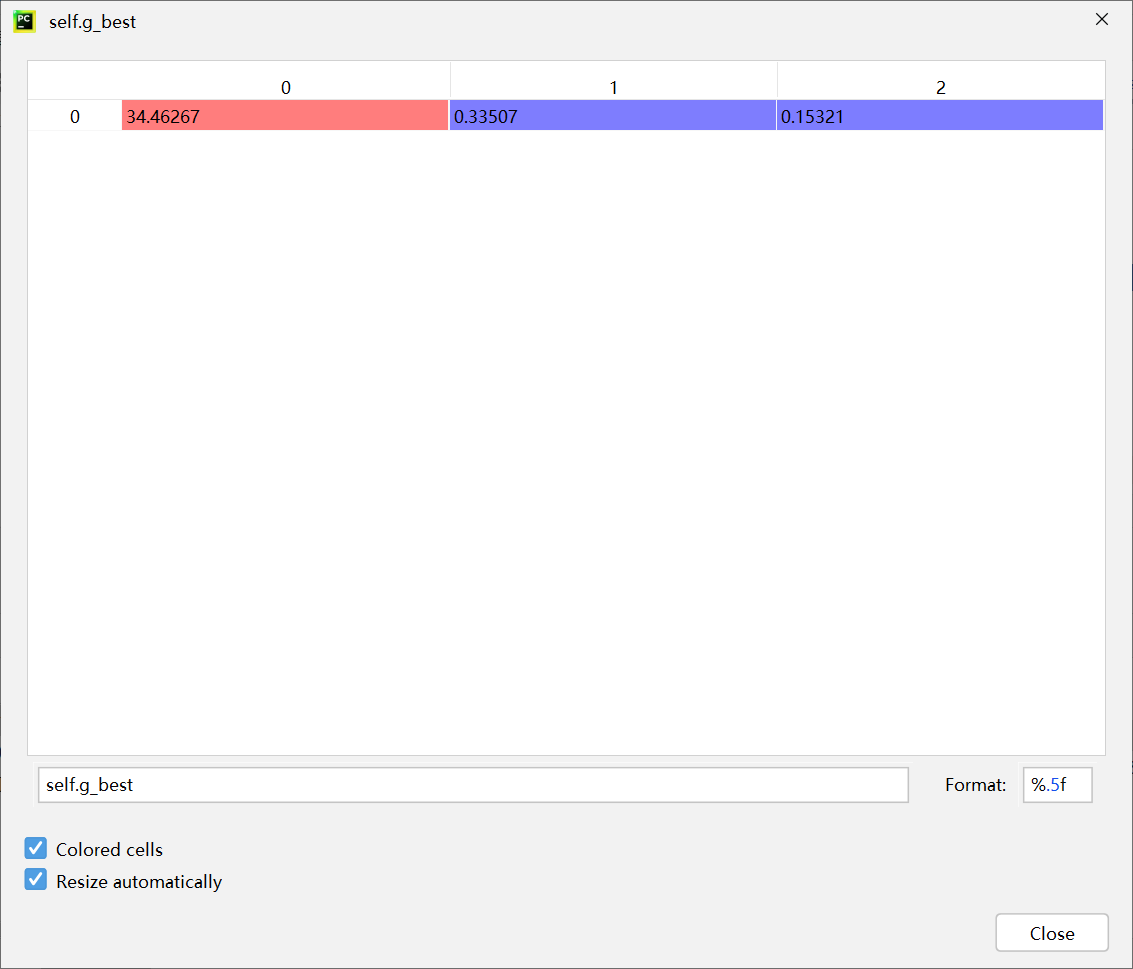
global best并没有发生改变
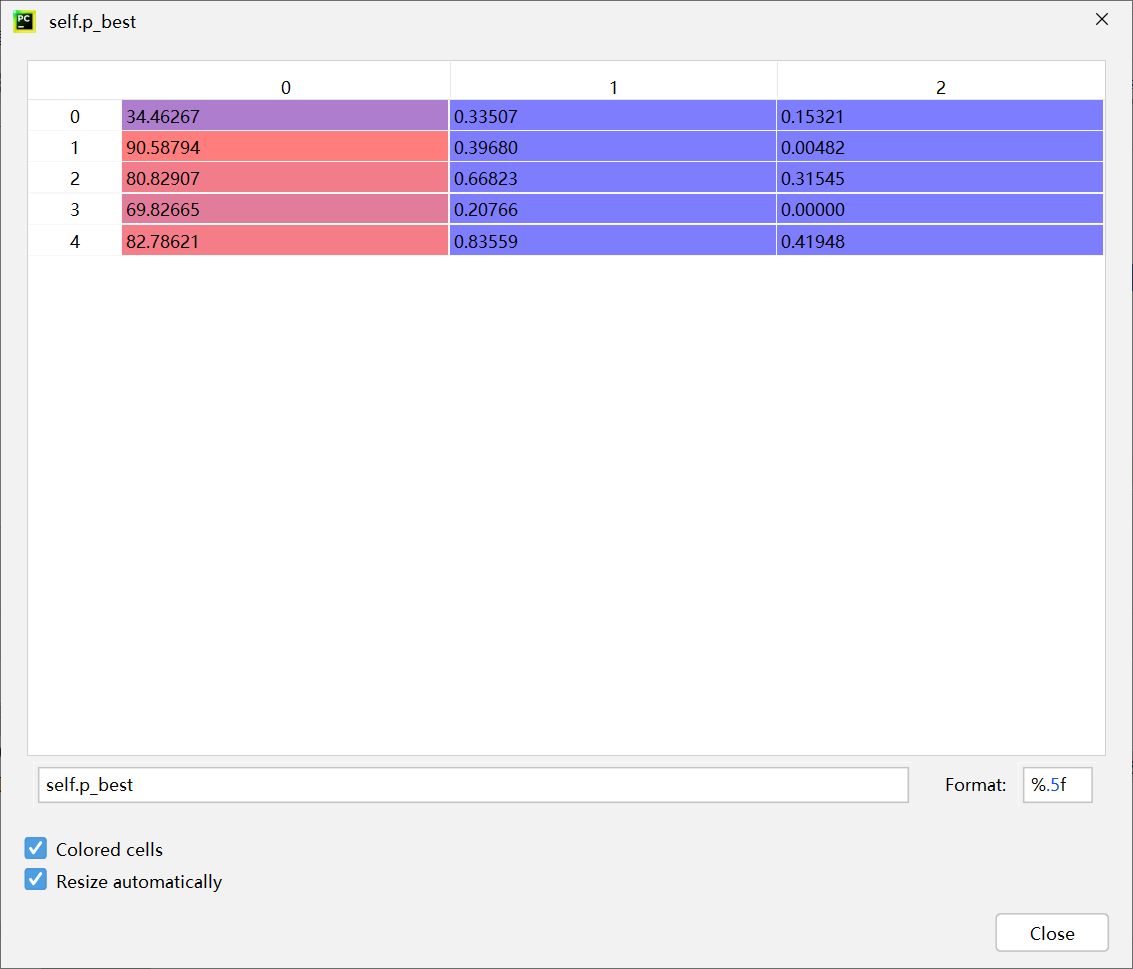
fitness:
[0.9719047619047618, 0.9663492063492063, 0.9607936507936508, 0.9607936507936508, 0.9607936507936508]
第三次迭代
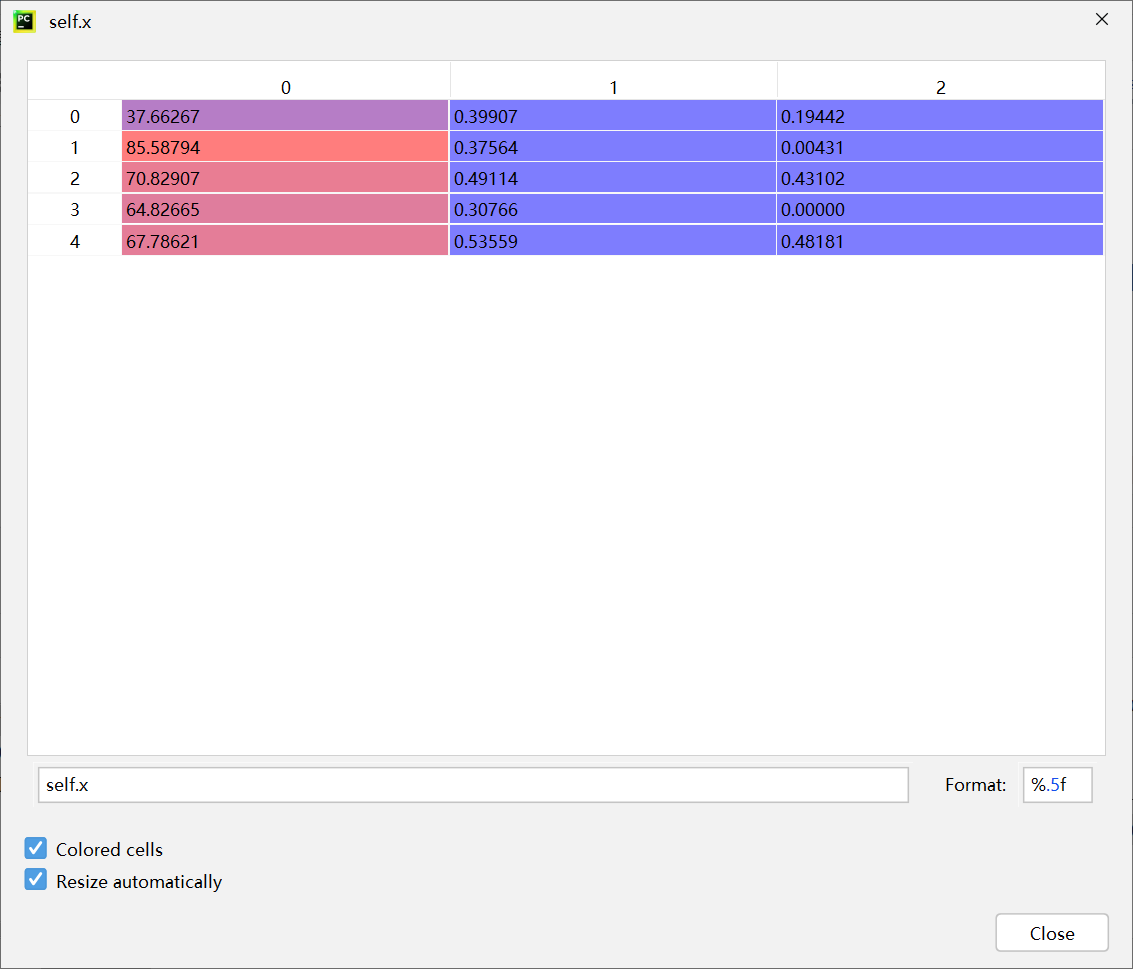
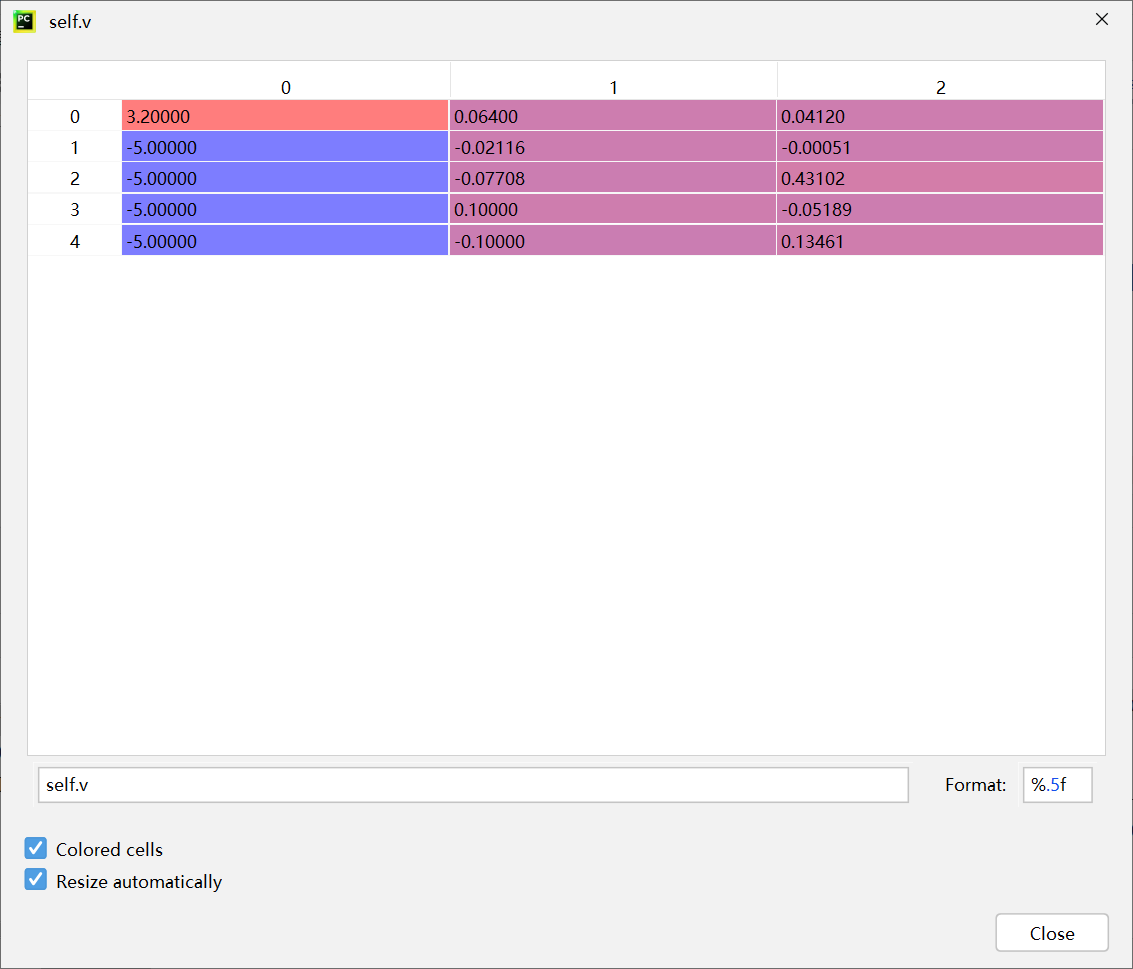
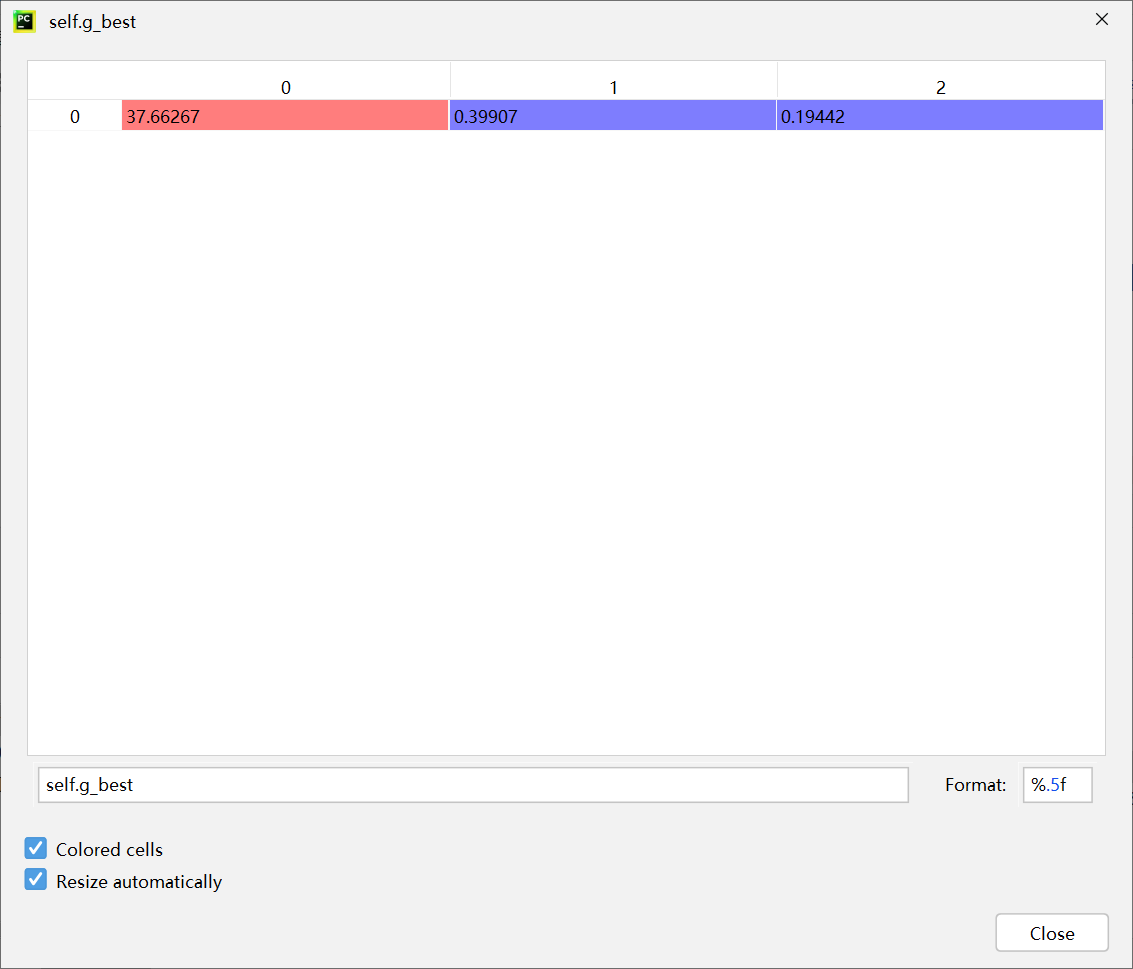
fitness:0.9719047619047618
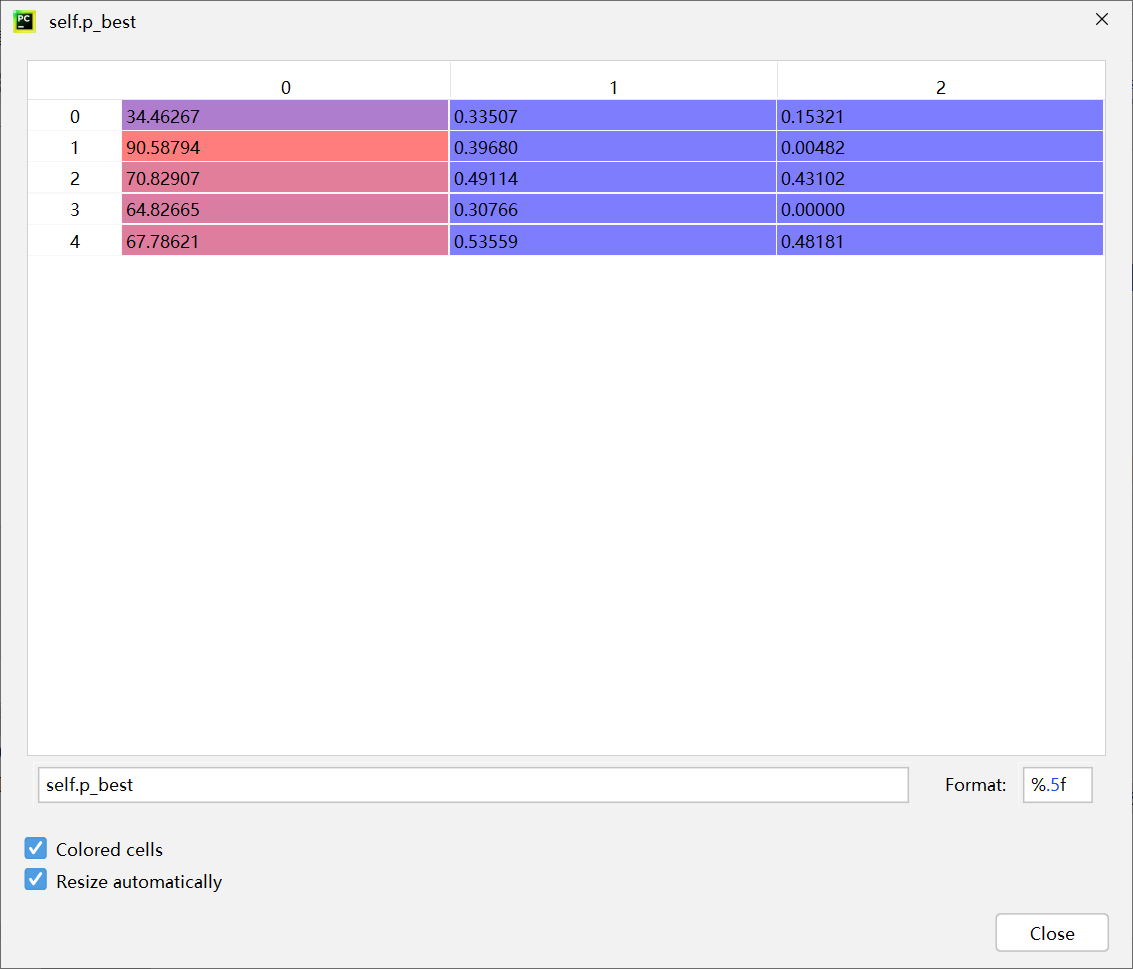
fitness:
[0.9719047619047618, 0.9663492063492063, 0.9663492063492063, 0.9663492063492063, 0.9663492063492063]
第四次迭代
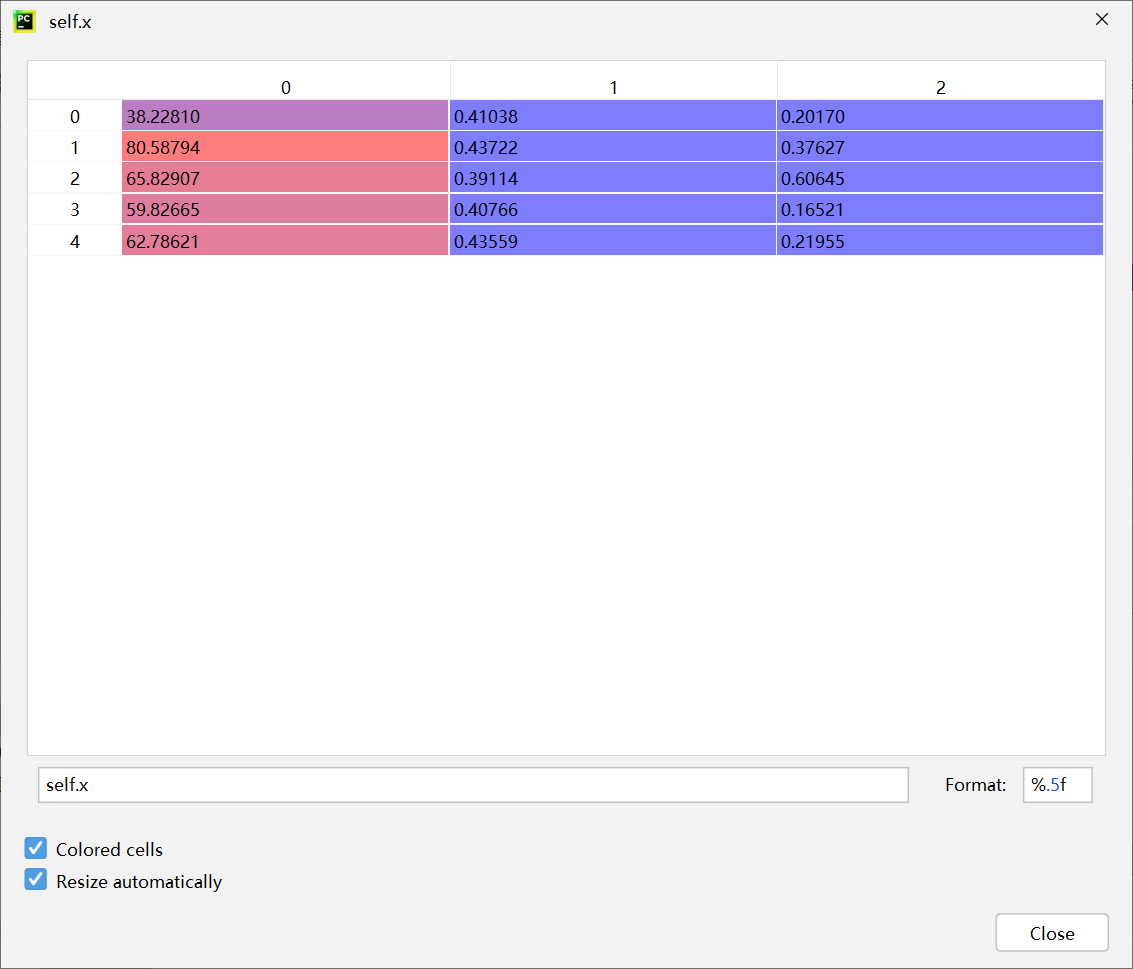
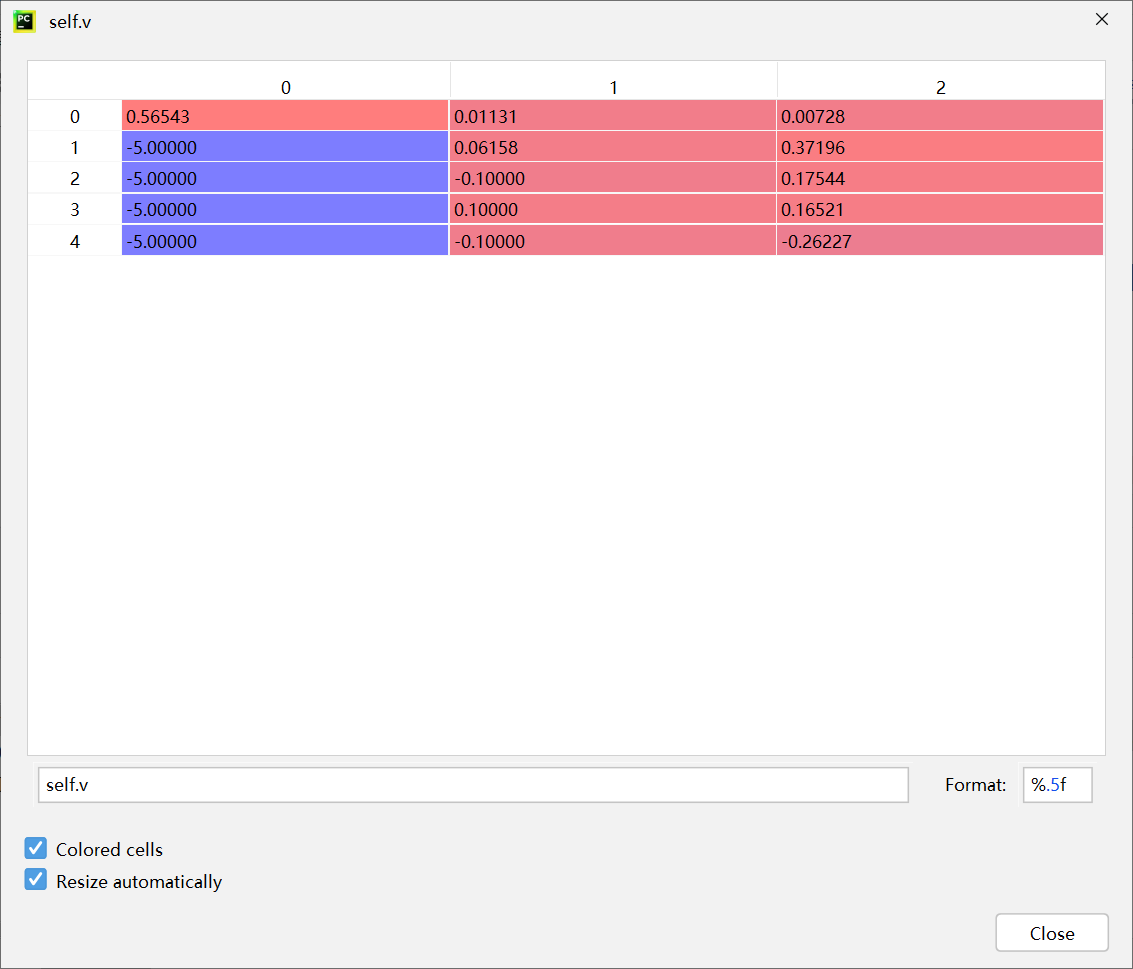
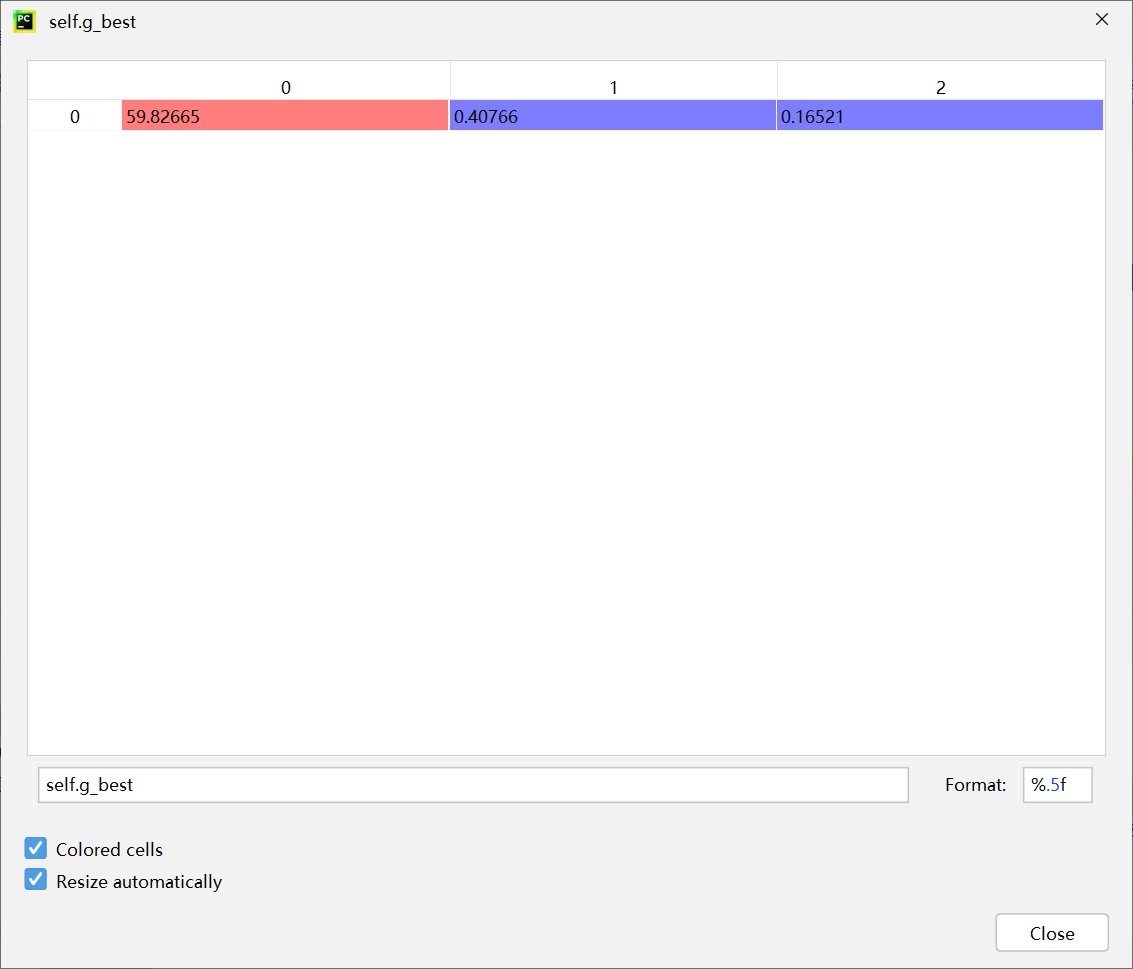
fitness:0.9720634920634922
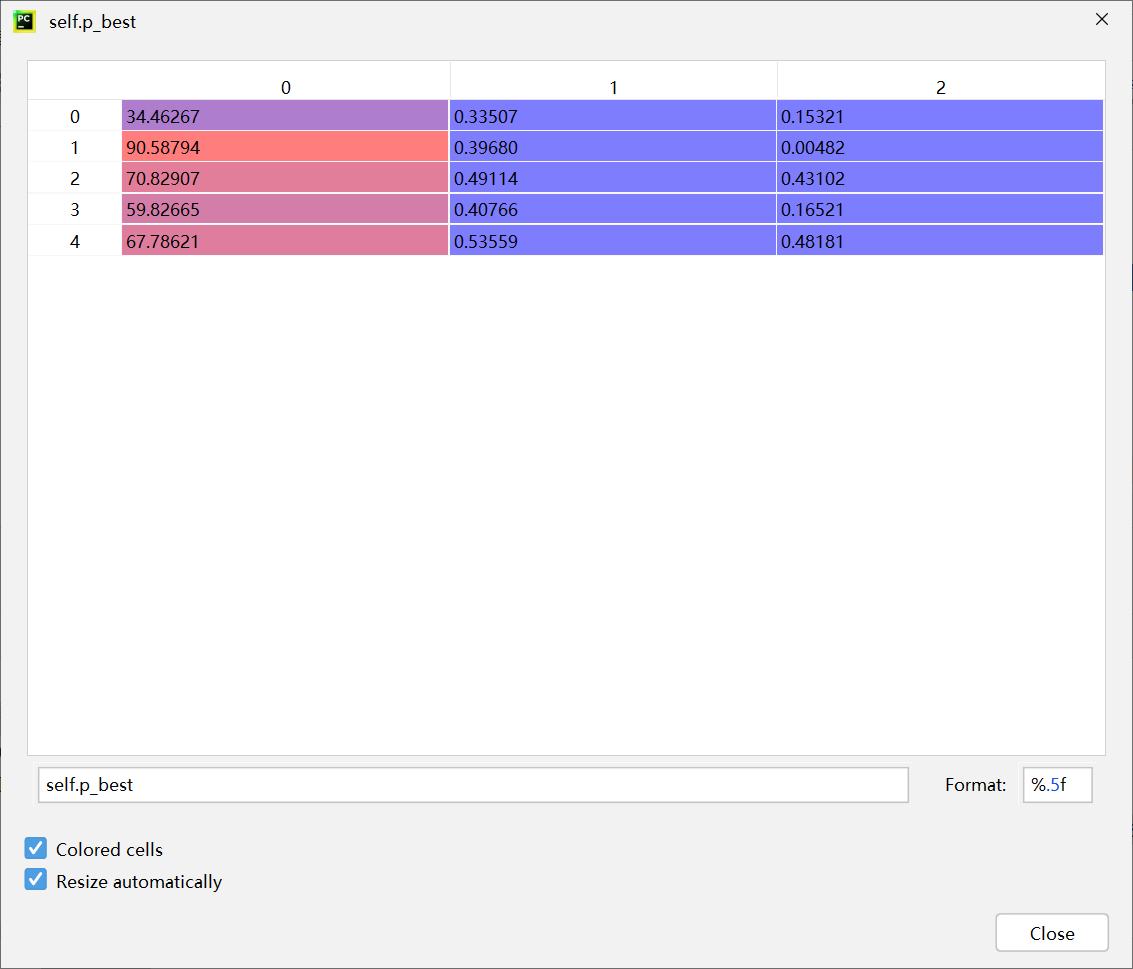
[0.9719047619047618, 0.9663492063492063, 0.9663492063492063, 0.9720634920634922, 0.9663492063492063]
第五次迭代
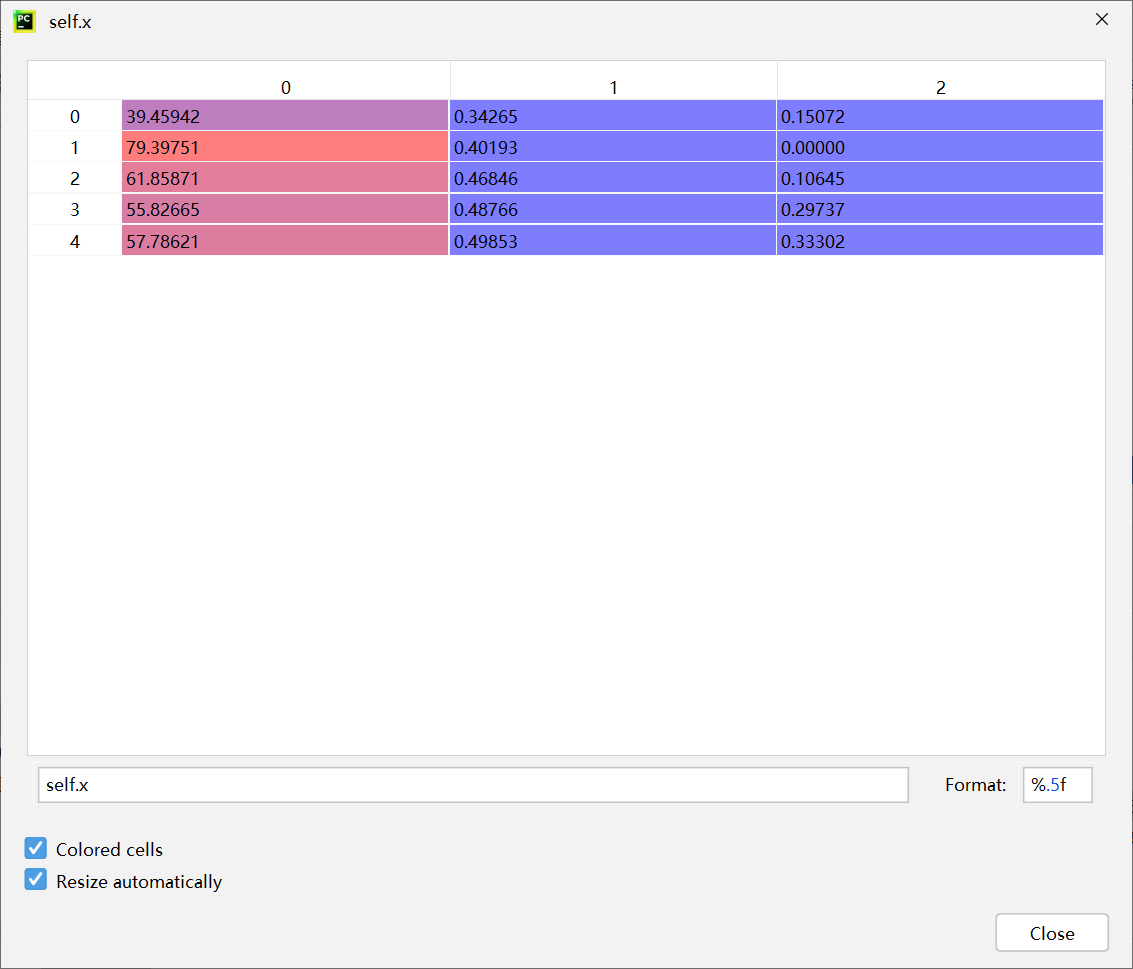
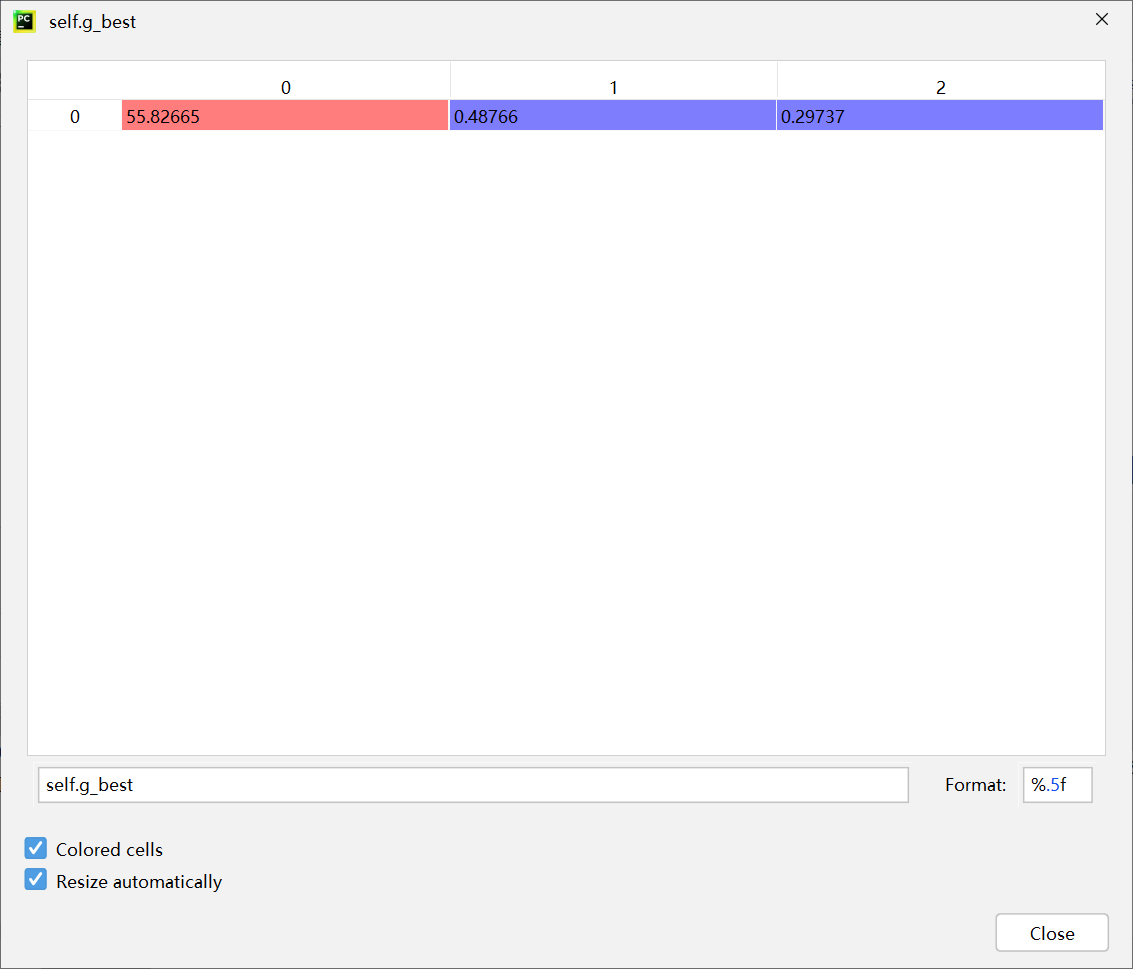
0.9720634920634922
[0.9719047619047618, 0.9663492063492063, 0.9663492063492063, 0.9720634920634922, 0.9720634920634922]


 浙公网安备 33010602011771号
浙公网安备 33010602011771号