bzoj 1001 [BeiJing2006]狼抓兔子 最小割+最短路

题面

题目传送门

解法

将最大流转化成最小割，然后跑最短路即可

具体如何见图可以参考下图

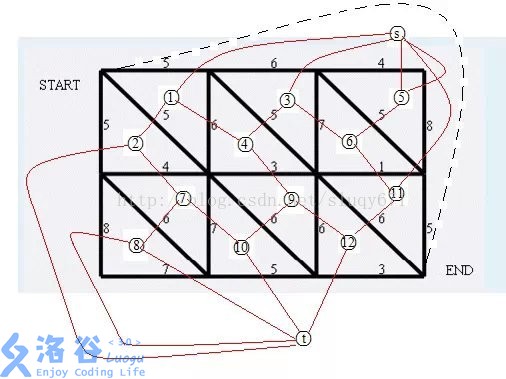
尽量用dijkstra

代码

#include <bits/stdc++.h>
#define PI pair <int, int>
#define mp make_pair
#define N 1010
using namespace std;
template <typename node> void chkmax(node &x, node y) {x = max(x, y);}
template <typename node> void chkmin(node &x, node y) {x = min(x, y);}
template <typename node> void read(node &x) {
	x = 0; int f = 1; char c = getchar();
	while (!isdigit(c)) {if (c == '-') f = -1; c = getchar();}
	while (isdigit(c)) x = x * 10 + c - '0', c = getchar(); x *= f;
}
struct Edge {
	int next, num, v;
} e[N * N * 8];
struct Node {
	int x, y;
} a[N][N];
int s, t, cnt, dis[2 * N * N], used[2 * N * N];
void add(int x, int y, int v) {
	e[++cnt] = (Edge) {e[x].next, y, v};
	e[x].next = cnt;
}
int dijkstra() {
	for (int i = 0; i <= t; i++)
		dis[i] = INT_MAX, used[i] = 0;
	priority_queue <PI, vector <PI>, greater <PI> > h;
	h.push(mp(0, s)); dis[s] = 0;
	while (!h.empty()) {
		PI tmp = h.top(); h.pop();
		int x = tmp.second;
		if (used[x]) continue; used[x] = 1;
		for (int p = e[x].next; p; p = e[p].next) {
			int k = e[p].num, v = e[p].v;
			if (dis[k] > dis[x] + v) {
				dis[k] = dis[x] + v;
				h.push(mp(dis[k], k));
			}
		}
	}
	return dis[t];
}
int main() {
	int n, m; read(n), read(m);
	if (n == 1 && m == 1) {
		cout << "0\n";
		return 0;
	}
	s = 0, t = cnt = (n - 1) * (m - 1) * 2 + 1;
	int tot = 0;
	for (int i = 1; i < n; i++)
		for (int j = 1; j < m; j++)
			a[i][j].x = ++tot, a[i][j].y = ++tot;
	for (int i = 1; i <= n; i++)
		for (int j = 1; j < m; j++) {
			int x; read(x);
			if (i == 1) add(s, a[1][j].x, x);
			if (i == n) add(a[i - 1][j].y, t, x);
			if (i > 1 && i < n) add(a[i - 1][j].y, a[i][j].x, x), add(a[i][j].x, a[i - 1][j].y, x);
		}
	for (int i = 1; i < n; i++)
		for (int j = 1; j <= m; j++) {
			int x; read(x);
			if (j == 1) add(a[i][j].y, t, x);
			if (j == m) add(s, a[i][j - 1].x, x);
			if (j > 1 && j < m) add(a[i][j - 1].x, a[i][j].y, x), add(a[i][j].y, a[i][j - 1].x, x);
		}
	for (int i = 1; i < n; i++)
		for (int j = 1; j < m; j++) {
			int x; read(x);
			add(a[i][j].x, a[i][j].y, x);
			add(a[i][j].y, a[i][j].x, x);
		}
	cout << dijkstra() << "\n";
	return 0;
}