算法实验报告3
算法分析与设计实验报告
曹王欣 18030100167 计算机科学与技术
实验三 地理路由(map routing)
- 实验目的
实现经典的 Dijkstra 最短路径算法,并对其进行优化。 这种算法广泛应用于地理信息系统(GIS),包括 MapQuest 和基于 GPS 的汽车导航系统。
目标:
优化 Dijkstra 算法,使其可以处理给定图的数千条最短路径查询。
一旦你读取图(并可选地预处理),你的程序应该在亚线性时间内解决最短路径问题。一种方法是预先计算出所有顶点对的最短路径;然而,你无法承受存储所有这些信息所需的二次空间。你的目标是
减少每次最短路径计算所涉及的工作量,而不会占用过多的空间。 建议你选择下面的一些潜在想法来实现,或者你可以开发和实现自己的想法。
想法 1. Dijkstra 算法的朴素实现检查图中的所有 V 个顶点。 减少检查的顶点数量的一种策略是一旦发现目的地的最短路径就停止搜索。 通过这种方法,可以使每个最短路径查询的运行时间与 E' log V'成比例,其中 E'和 V'是 Dijkstra 算法检查的边和顶点数。 然而,这需
要一些小心,因为只是重新初始化所有距离为∞就需要与 V 成正比的时间。由于你在不断执行查询,因而只需重新初始化在先前查询中改变的那些值来大大加速查询。
想法 2. 你可以利用问题的欧式几何来进一步减少搜索时间,这在算法书的第 4.4 节描述过。对于一般图,Dijkstra 通过将 d[w]更新为 d[v] + 从 v 到 w 的距离来松弛边 v-w。 对于地图,则将 d[w]更新为 d[v] + 从 v 到 w 的距离 + 从 w 到 d 的欧式距离 −从 v 到 d 的欧式距离。
这种方法称之为 A*算法。这种启发式方法会有性能上的影响,但不会影响正确性。
想法 3. 使用更快的优先队列。 在提供的优先队列中有一些优化空间。 你也可以考虑使用 Sedgewick 程序中的多路堆(Multiway heaps, Section 2.4)。
测试。 美国大陆文件 usa.txt 包含 87,575 个交叉口和 121,961 条道路。 图形非常稀疏 - 平均的度为 2.8。 你的主要目标应该是快速回答这个网络上的顶点对的最短路径查询。
算法可能会有不同执行时间,这取决于两个顶点是否在附近或相距较远。 我们提供测试这两种情况的输入文件。 你可以假设所有的 x 和 y 坐标都是 0 到 10,000 之间的整数。
- 实验环境
Java8 Eclipse algs4.jar包
- 实验内容与代码实现
首先我们要实现Dijkstra算法,为了实现该算法,我们首先需要实现存图用的数据结构EuclideanGraph.java和该题中每一个点的数据结构Point.java
在Point.java中,我们存入每一个点的x,y坐标,同时实现Point.distance方法,用于计算点对的坐标
public class Point {
private final static double SCALEX = 0.0001 * 1000.0;
private final static double SCALEY = 0.0001 * 1000.0 * 1.3;
private int x; // x component,X坐标
private int y; // y component,y坐标
public Point(int x, int y) { this.x = x; this.y = y; }
// convert to string
public String toString() {
return "(" + x + ", " + y + ")";
}
// return Euclidean distance between this and p
public double distanceTo(Point p) {
double dx = this.x - p.x;
double dy = this.y - p.y;
return Math.sqrt(dx*dx + dy*dy);
}
// plot in turtle graphics,用于画图的程序
public void draw() {
Turtle.fly(x * SCALEX, y * SCALEY);
Turtle.spot(2);
}
// draw line from this to q in Turtle graphics
public void drawTo(Point q) {
Point p = this;
Turtle.fly(p.x * SCALEX, p.y * SCALEY);
Turtle.go (q.x * SCALEX, q.y * SCALEY);
}
}
然后,我们实现存图用的EuClideanGraph.java,我们需要实现迭代器方法neighbor,返回邻接表每一个节点的迭代器,在java中我们没有c++的vector类型,所以,我们自己写hasnext和next方法来实现邻接表的迭代(需要先写个接口保证安全性),而每一个节点的邻接节点使用头插法进行插入,我们还利用了turtle库进行画图操作,这是Sedgewick提供的方法,我没有进行改动,当然,我们不必存边的长度,因为长度可以用Point中distance方法直接求出来,这样我们也节省了存储空间
public interface IntIterator {
int next();
boolean hasNext();
}
import java.io.File;
import java.io.IOException;
import java.util.Scanner;
/*************************************************************************
* Compilation: javac EuclideanGraph.java
* Execution: java EuclideanGraph
* Dependencies: In.java IntIterator.java
*
* Undirected graph of points in the plane, where the edge weights
* are the Euclidean distances.
*
*************************************************************************/
public class EuclideanGraph {
// for portability
private final static String NEWLINE = System.getProperty("line.separator");
private int V; // number of vertices
private int E; // number of edges
private Node[] adj; // adjacency lists
private Point[] points; // points in the plane
// node helper class for adjacency list
private static class Node {
int v;
Node next;
Node(int v, Node next) { this.v = v; this.next = next; }
}
// iterator for adjacency list
private class AdjListIterator implements IntIterator {
private Node x;
AdjListIterator(Node x) { this.x = x; }
public boolean hasNext() { return x != null; }
public int next() {
int v = x.v;
x = x.next;
return v;
}
}
/*******************************************************************
* Read in a graph from a file, bare bones error checking.
* V E
* node: id x y
* edge: from to
*******************************************************************/
public EuclideanGraph(int M,int N,int VV[],int XX[],int YY[],int MM[],int NN[]) {
V = M;
E = N;
// read in and insert vertices
points = new Point[V];
for (int i = 0; i < V; i++) {
int v = VV[i];
int x = XX[i];
int y = YY[i];
if (v < 0 || v >= V) throw new RuntimeException("Illegal vertex number");
points[v] = new Point(x, y);
}
// read in and insert edges
adj = new Node[V];
for (int i = 0; i < E; i++) {
int v = MM[i];
int w = NN[i];
if (v < 0 || v >= V) throw new RuntimeException("Illegal vertex number");
if (w < 0 || w >= V) throw new RuntimeException("Illegal vertex number");
adj[v] = new Node(w, adj[v]);
adj[w] = new Node(v, adj[w]);
}
}
// accessor methods
public int V() { return V; }
public int E() { return E; }
public Point point(int i) { return points[i]; }
// Euclidean distance from v to w
public double distance(int v, int w) { return points[v].distanceTo(points[w]); }
// return iterator for list of neighbors of v
public IntIterator neighbors(int v) {
return new AdjListIterator(adj[v]);
}
// string representation - takes quadratic time because of string concat
public String toString() {
String s = "";
s += "V = " + V + NEWLINE;
s += "E = " + E + NEWLINE;
for (int v = 0; v < V && v < 100; v++) {
String t = v + " " + points[v] + ": ";
for (Node x = adj[v]; x != null; x = x.next)
t += x.v + " ";
s += t + NEWLINE;
}
return s;
}
// draw the graph in turtle graphics
public void draw() {
for (int v = 0; v < V; v++) {
points[v].draw();
for (Node x = adj[v]; x != null; x = x.next) {
int w = x.v;
points[v].drawTo(points[w]);
}
}
Turtle.render();
}
// test client
}
下面我们实现索引优先队列,这里我直接使用了书上的源码
/*********************************************************************
* Indirect priority queue.
*
* The priority queue maintains its own copy of the priorities,
* unlike the one in Algorithms in Java.
*
* This code is from "Algorithms in Java, Third Edition,
* by Robert Sedgewick, Addison-Wesley, 2003.
*********************************************************************/
public class IndexPQ {
private int N; // number of elements on PQ
private int[] pq; // binary heap
private int[] qp; //
private double[] priority; // priority values
public IndexPQ(int NMAX) {
pq = new int[NMAX + 1];
qp = new int[NMAX + 1];
priority = new double[NMAX + 1];
N = 0;
}
public boolean isEmpty() { return N == 0; }
// insert element k with given priority
public void insert(int k, double value) {
N++;
qp[k] = N;
pq[N] = k;
priority[k] = value;
fixUp(pq, N);
}
// delete and return the minimum element
public int delMin() {
exch(pq[1], pq[N]);
fixDown(pq, 1, --N);
return pq[N+1];
}
// change the priority of element k to specified value
public void change(int k, double value) {
priority[k] = value;
fixUp(pq, qp[k]);
fixDown(pq, qp[k], N);
}
/**************************************************************
* General helper functions
**************************************************************/
private boolean greater(int i, int j) {
return priority[i] > priority[j];
}
private void exch(int i, int j) {
int t = qp[i]; qp[i] = qp[j]; qp[j] = t;
pq[qp[i]] = i; pq[qp[j]] = j;
}
/**************************************************************
* Heap helper functions
**************************************************************/
private void fixUp(int[] a, int k) {
while (k > 1 && greater(a[k/2], a[k])) {
exch(a[k], a[k/2]);
k = k/2;
}
}
private void fixDown(int[] a, int k, int N) {
int j;
while (2*k <= N) {
j = 2*k;
if (j < N && greater(a[j], a[j+1])) j++;
if (!greater(a[k], a[j])) break;
exch(a[k], a[j]);
k = j;
}
}
}
下面,我们实现Dijkstra方法,Dijkstra 算法是最短路径问题的经典解决方案,教科书 4.4 节描述了该算法。
基本思路不难理解。对于图中的每个顶点,我们维护从源点到该顶点的最短已知的路径长度,并且将这些长度保持在优先队列(priority queue, PQ)中。 初始时,我们把所有的顶点放在这个队列中,并设置高优先级,然后将源点的优先级设为 0.0。 算法通过从 PQ 中取出最低优先级的顶点,然后检查可从该顶点经由一条边可达的所有顶点,以查看这条边是否提供了从源点到那个顶点较之之前已知的最短路径的更短路径。 如果是这样,它会降低优先级来反映这种新的信息,同时我们需要在每次求出我们需要的边的时候更新节点的父亲数组PRE,用来存储经过的路径。
import java.awt.Color;
public class Dijkstra {
private static double INFINITY = Double.MAX_VALUE;
private static double EPSILON = 0.000001;
private EuclideanGraph G;
private double[] dist;
private int[] pred;
public Dijkstra(EuclideanGraph G) {
this.G = G;
}
// return shortest path distance from s to d
public double distance(int s, int d) {
dijkstra(s, d);
return dist[d];
}
// print shortest path from s to d (interchange s and d to print in right order)
public void showPath(int d, int s) {
dijkstra(s, d);
if (pred[d] == -1) {
System.out.println(d + " is unreachable from " + s);
return;
}
for (int v = d; v != s; v = pred[v])
System.out.print(v + "-");
System.out.println(s);
}
// plot shortest path from s to d
public void drawPath(int s, int d) {
dijkstra(s, d);
if (pred[d] == -1) return;
Turtle.setColor(Color.red);
for (int v = d; v != s; v = pred[v])
G.point(v).drawTo(G.point(pred[v]));
Turtle.render();
}
// Dijkstra's algorithm to find shortest path from s to d
private void dijkstra(int s, int d) {
int V = G.V();
// initialize
dist = new double[V];
pred = new int[V];
for (int v = 0; v < V; v++) dist[v] = INFINITY;
for (int v = 0; v < V; v++) pred[v] = -1;
// priority queue
IndexPQ pq = new IndexPQ(V);
for (int v = 0; v < V; v++) pq.insert(v, dist[v]);
// set distance of source
dist[s] = 0.0;
pred[s] = s;
pq.change(s, dist[s]);
// run Dijkstra's algorithm
while (!pq.isEmpty()) {
int v = pq.delMin();
//// System.out.println("process " + v + " " + dist[v]);
// v not reachable from s so stop
if (pred[v] == -1) break;
// scan through all nodes w adjacent to v
IntIterator i = G.neighbors(v);
while (i.hasNext()) {
int w = i.next();
if (dist[v] + G.distance(v, w) < dist[w] - EPSILON) {
dist[w] = dist[v] + G.distance(v, w);
pq.change(w, dist[w]);
pred[w] = v;
//// System.out.println(" lower " + w + " to " + dist[w]);
}
}
}
}
}
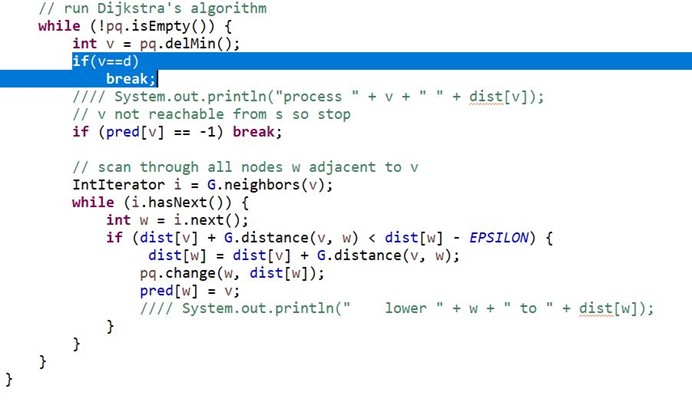
针对改进1,我们的目标是求S和D之间的最短路径,所以并不需要把S到所有节点的最短路径求出来,所以,我们可以加一个判断条件,当PQ.delmin()输出的节点是D的时候直接退出。
观察下图代码,其实就是把Dijsktra算法的加了两行,而我们重点标出的地方就是算法的改进实现
![]()
针对改进2,此时我们更改dist数组的定义,我们的目标是求s与d之间的最短路径,那么在这个几何平面上,我们不妨定义dist[V]现在不是S到V之间的最短距离,而是S到V的最短距离+V到D的直接距离的和
那么我们的判断条件变成了
if (dist[v] -G.distance(v, d)+ G.distance(v, w) +G.distance(w, d) < dist[w] ) {
dist[w] = dist[v] -G.distance(v, d)+ G.distance(v, w) +G.distance(w, d);
}
为什么是这样呢,因为
S到V的最短距离现在变成了 dist[v] -G.distance(v, d)
那么S到W的最短距离就是 dist[v] -G.distance(v, d)+ G.distance(v, w)
那么S到W的最短距离+W到d的最短距离就是
dist[v] -G.distance(v, d)+ G.distance(v, w) +G.distance(w, d)
这样每次更新数组的时候我们相当于进行了一次几何三角形判断,也就是此时的剪枝不断向着我们的目标dist[d]前进,所以我们的A*算法是正确的,这就是A*算法的证明
![]()
观察我们上面着重的地方,就是加入了这两行判断,进行了A*算法的启发式搜索
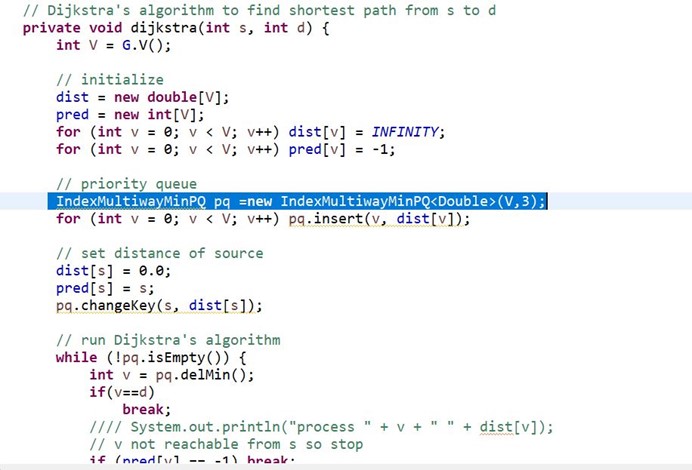
针对改进3,我们此时使用多路堆来改变单路堆来加速,我们此时使用IndexMultiwayMinPQ代替IndexPQ就行了,我们的IndexMultiwayMinPQ使用的是algs4.jar包中的实现,也就是教科书的源码,观察我们着重的地方,就是更改了堆的实现就能进行改进了
![]()
下面,我们书写我们的主程序,我们采用文件输入输出的方法,直接从test.txt中读取我们的数据(我更改了我们输入文件的文件名),然后打印出每一种算法的时间,以及他们所实现的最短路径
import java.io.File;
import java.io.IOException;
import java.util.Scanner;
/*************************************************************************
* Compilation: javac Distances.java
* Execution: java Distances file < input.txt
* Dependencies: EuclideanGraph.java Dijkstra.java In.java StdIn.java
*
* Reads in a map from a file, and repeatedly reads in two integers s
* and d from standard input, and prints the distance of the shortest
* path from s to d to standard output.
*
****************************************************************************/
public class Distances {
public static void main(String[] args) throws IOException {
File file = new File("C:\\test.txt");
Scanner input = new Scanner(file);
int V = input.nextInt();
int E = input.nextInt();
int[] VV = new int[V];
int[] XX = new int[V];
int[] YY = new int[V];
int[] MM = new int[E];
int[] NN = new int[E];
for(int i=0;i<V;i++)
{
VV[i] = input.nextInt();
XX[i] = input.nextInt();
YY[i] = input.nextInt();
}
for(int i=0;i<E;i++)
{
MM[i] = input.nextInt();
NN[i] = input.nextInt();
}
EuclideanGraph G = new EuclideanGraph(V,E,VV,XX,YY,MM,NN);
int s = 1;
int d = 500;
Dijkstra dijkstra = new Dijkstra(G);
Dijkstra1 dijkstra1 = new Dijkstra1(G);
Dijkstra2 dijkstra2 = new Dijkstra2(G);
Dijkstra3 dijkstra3 = new Dijkstra3(G);
System.out.println(dijkstra.distance(s, d));
long starttime,endtime,realtime;
starttime = System.currentTimeMillis();
dijkstra.showPath(s, d);
endtime = System.currentTimeMillis();
realtime = endtime - starttime;
System.out.println("普通算法"+realtime+"ms");
starttime = System.currentTimeMillis();
dijkstra1.showPath(s, d);
endtime = System.currentTimeMillis();
realtime = endtime - starttime;
System.out.println("改进1为"+realtime+"ms");
starttime = System.currentTimeMillis();
dijkstra2.showPath(s, d);
endtime = System.currentTimeMillis();
realtime = endtime - starttime;
System.out.println("改进2为"+realtime+"ms");
starttime = System.currentTimeMillis();
dijkstra3.showPath(s, d);
endtime = System.currentTimeMillis();
realtime = endtime - starttime;
System.out.println("改进3为"+realtime+"ms");
//dijkstra.drawPath(s, d); input.close();
}
}
- 实验结果截图
![]()
![]()
我们选定1号节点到500号节点,输出的最短距离为393.8544,路径为1-4-18-34-37-46-50-57-78-84-87-94-120-125-143-169-183-206-215-232-271-278-279-285-303-312-340-360-410-422-441-459-479-514-542-522-498-497-496-493-495-521-517-510-500
普通算法40ms,改进1为6ms,改进2为6ms,改进3为28ms,说明我们的改进起到了剪枝的效果,成功进行了算法改进
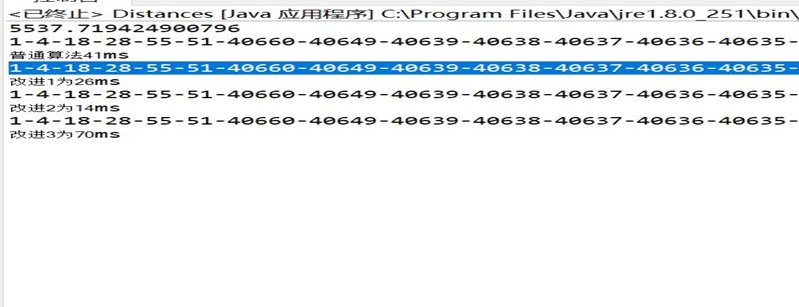
下面,我们变成1到10000号节点,最短路径的输出为
1-4-18-28-55-51-40660-40649-40639-40638-40637-40636-40635-40626-40625-40624-40628-40627-40629-40623-40616-40599-71890-71879-71839-71822-71814-71763-71762-71755-71753-71725-71721-71717-71712-71703-71699-71698-71697-3257-3255-3256-3250-3248-3228-3231-3192-3186-3210-3209-3203-3199-3200-3205-3204-3206-3202-3189-3188-3180-3165-3197-3208-3219-3223-3235-3292-3309-3310-3286-3288-3296-3295-3294-3285-3277-3276-3272-3245-3244-3242-3240-3212-3191-3181-3185-3187-3216-3225-3183-3179-3174-3171-3175-3176-3168-3163-3162-3157-3156-3144-3141-3136-3135-3134-3130-61588-61515-61516-61518-61519-61513-61453-61455-61459-61458-61461-61465-61489-61510-61546-61545-61543-61542-61541-61551-61547-61561-61604-61605-61614-61609-61611-61610-61612-61613-61608-61589-61544-61531-61521-61512-61493-61492-61498-61472-61473-61479-61487-61500-61506-61507-61504-61502-61505-61508-61501-61466-61433-61429-61426-61401-61393-61396-61387-61403-61397-61383-61384-61391-61406-61407-61427-61428-61432-61468-61565-61571-61572-61576-61577-61579-61607-61638-61653-61665-61690-61692-61693-72018-72021-72022-72024-72023-72079-72078-72083-72084-72082-72081-72077-72093-72052-72040-72038-72036-72037-72046-72054-72058-72059-72062-72061-72060-72056-72055-72066-72067-72072-72070-72069-72068-72041-72014-72000-72085-48106-48120-48173-48121-48125-48126-48122-48123-48124-48136-48144-48151-48157-48253-48307-48332-48338-48333-48325-48322-48318-48315-48317-48314-48306-48233-48219-48249-48291-48288-48283-48280-48273-48269-48267-48262-48257-48240-48231-48224-48222-48221-48228-48227-48226-48223-48198-48252-48259-48292-48294-48299-48321-48324-48303-48232-48393-48396-48432-48433-1900-1905-1904-1899-1885-1886-1890-1891-1892-1894-1889-1876-1880-1882-1879-1873-1875-1877-1878-1866-1855-1858-1862-1861-1857-1854-1856-1860-1864-1901-1906-1916-1920-1921-1939-1963-1961-1962-1964-1998-10846-10841-10840-10842-10844-10845-10843-10666-10767-10769-10662-10658-10638-10636-10629-10594-10586-10551-10544-10511-10344-10323-9984-9967-9920-9855-9915-9914-9900-9853-9851-9850-9837-9831-9832-9833-9829-9802-9787-9759-9768-9817-9792-9966-10017-10022-10088-10092-10091-10090-10100-10095-10093-10146-10147-10151-10143-10048-10049-9985-9982-9973-9977-9971-9947-9932-9934-9980-9996-10019-10023-10020-9998-10000
![]()
普通算法41ms,改进1为26ms,改进2为14ms,改进3为70ms,这时候我们发现,三路堆不一定比2路堆来的快,而A*算法起到的作用非常明显,这说明启发式搜索的巨大作用。
综上,我们完成了此次map routing的算法实验,我们比较了三种改进方案,并且亲自实现迪杰斯特拉算法,我们的结论是启发式搜索的作用是巨大的





 浙公网安备 33010602011771号
浙公网安备 33010602011771号