深度学习——卷积神经网络[10]
目录
- 计算机视觉问题
- 边缘检测实例和卷积计算
- padding对图像填充
- 步幅stride
- 交相关cross-correlation和卷积
- 在立体volumn上做卷积
- 构建单层卷积神经网络
- pooling池化操作
- 卷积神经网络示例(全连接层)
- 为什么用卷积神经网络
一、计算视觉问题
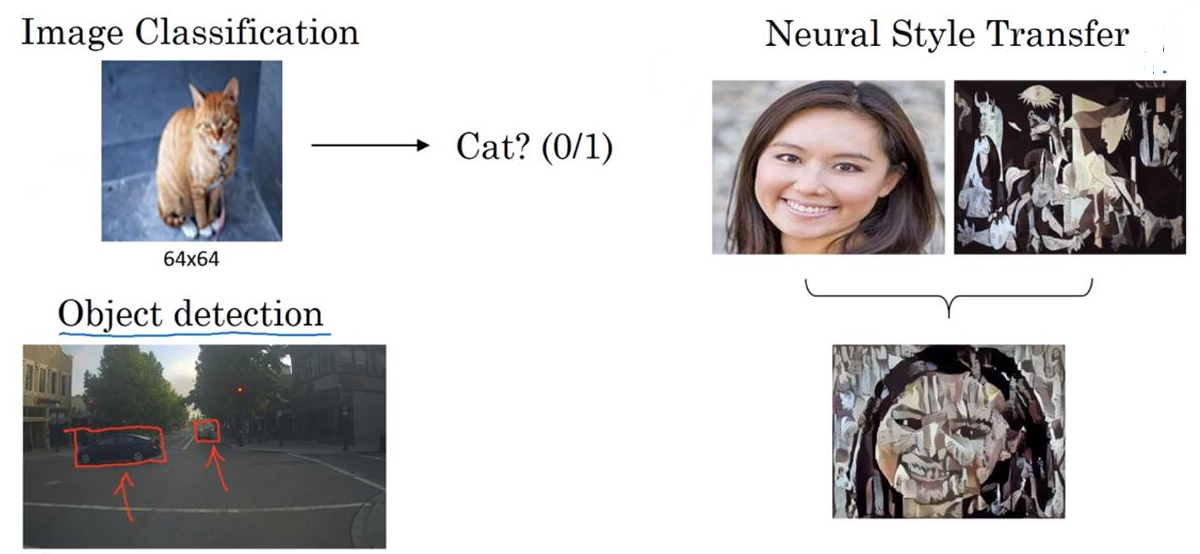
例子:图像分类,风格迁移,对象检测等
计算机视觉是对输入的图像/视频输出对它的处理或理解
计算机视觉的一个巨大挑战是数据量很大,很难找到足够多的数据来防止网络过拟合,输入/参数等数据量大需要很大的内存开销
二、边缘检测实例和卷积计算
在学习时前面的层会先学习低层的特征,然后再慢慢学习高层的特征
边缘检测:识别物体的边界,比如下面可以先识别出人/铁栏杆边界(垂直或水平方向)

如何识别垂直边缘,利用卷积计算convolution
左边是一张灰度图6x6的像素,中间是一个3x3的矩阵(作为过滤器),每次将左边的一个3x3子矩阵与filter各个值分别相乘得到和即为结果中的一位,最后是一个4x4矩阵。子矩阵每次向右(下)移一格,结果也向右(下)移一格
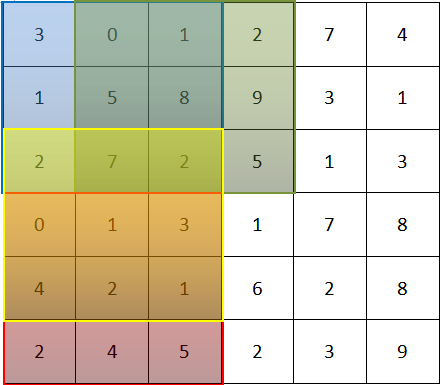 |
* | 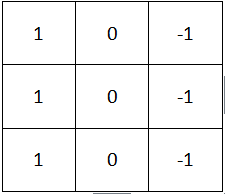 |
= | 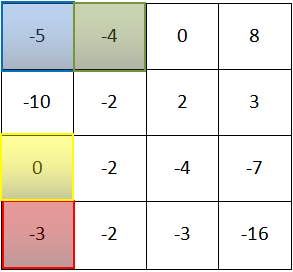 |
为什么这个可以作垂直检测
关键在于过滤器,1和-1可以相抵消,如果3个像素的跨度中颜色是一样的,那就会被抵消为0,如果不同,差距越大,结果中相应位置的值就越大。由此得到边缘
 |
* | 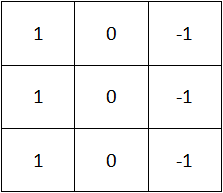 |
= |  |
| |
相同的filter,不同的输入,有明到暗也有暗到明
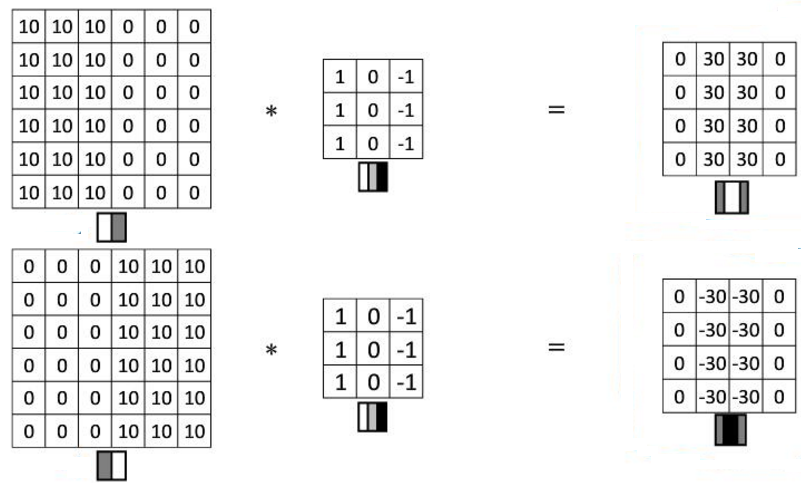
水平边缘检测过滤器
| 1 | 1 | 1 |
| 0 | 0 | 0 |
| -1 | -1 | -1 |
历史上对卷积使用的矩阵有不同的值,但是现在我们可以把矩阵中的值作为参数,通过学习来获得,这已经是计算机视觉中一个比较有效的方法
其实也可以学习出很多不同角度的边缘
|
|
||||||||||||||||||||||||
三、padding对图像填充
padding:卷积计算中的一个基本操作,就是对输入图像进行填充
为什么要填充?
1. 每次卷积计算后,图像大小就会缩小;2. 边缘的信息只用到了一次,会有损失
填充方法:通常是在图像四周再1个(多个)像素并以0填充
 |
* |  |
= |  |
| 输入图像 nxn n为原大小,p:填充的个数 | 卷积过滤器:fxf | 卷积结果:(n+2p-f+1)x(n+2p-f+1) |
两种填充类型
valid不填充:nxn * fxf —> (n-f+1)x(n-f+1)
same填充:使得输入和输出的大小一致。令n+2p-f+1=n,可得p = (f-1)/2
一般来说,在computer vision中filter矩阵维数是奇数:1.一个中心点;2. 这样可以对称填充,不用两边填充的像素个数不同
四、步幅stride
这个也是卷积计算中的一个基本操作,就是每次左边子矩阵移动的步长。如果得到的结果不是整除的,那么就用地板除,也就是向下取整(只对能被filter矩阵完整覆盖的区域进行计算)
| 输入 | 卷积过滤器 | 输出结果 |
|
图像大小:nxn padding: p stride:s |
fxf |
floor((n+2p-f)/s+1) xfloor((n+2p-f)/s+1) |
五、交相关cross-correlation和卷积
在数学上做卷积是需要对过滤器矩阵进行旋转的,但是在深度学习中人们习惯不进行旋转(这种更应该称为交相关,不过习惯上也称为了卷积)。在信号处理中结合率的性质很有用,但是在深度学习中并不是那么重要,这也是不进行旋转的理由

六、在立体volumn上做卷积
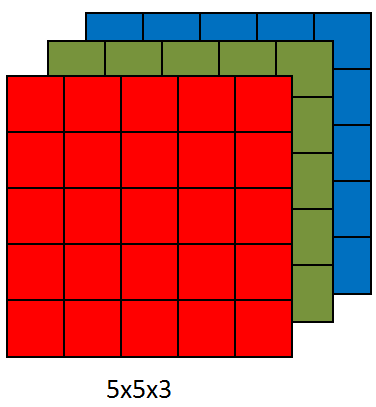
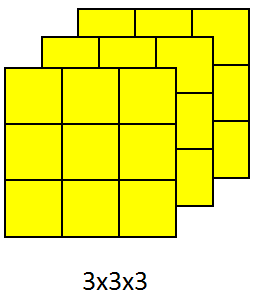
输入为一张RGB的图,高*宽*通道数(3通道),对应的filter也应该有3通道,各通道相对应,最后的结果是一个二维的矩阵,是把两个立方体中的数字对应相乘然后求和如果只关注红色构成的边界,可以把其它两通道的过滤器设置为0
 |
* |  |
= |  |
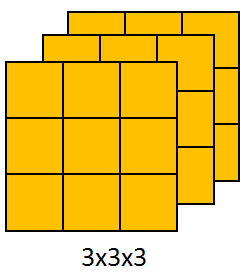
如果想一次检测多种特征,比如垂直+水平+45度等的做法:每个特征对应一个过滤器,分别与输入的矩阵相乘,然后把结果堆叠成立体的,各结果间并不再运算
注:有时也会把图像的通道数说成是深度
 |
* |  |
= |  |
 |
七、构建单层卷积神经网络
 |
* |  |
= | ReLU( +b1) +b1) |
-> |  |
| * |  |
= | ReLU( +b2) +b2) |
|||
| $x=a^{0}$ | $w^{[1]}$ |
$ReLU(z^{[1]})$ 每个过滤器有一个超参数b(实数) |
$a^{[1]}$ |
超参数个数
10个过滤器,均为3x3x3,则参数个数为(3x3x3+1)x10=280
符号表示说明
|
$f^{[l]}$过滤器大小 $p^{[l]}$padding大小 $s^{[l]}$步幅大小 $n^{[l]}_c$过滤器个数 过滤器:$f^{[l]}xf^{[l]}xn_c^{[l]}$ 激活结果:$a^{[l]}:n_H^{[l]}xn_w^{[l]}xn_c^{[l]}$ 权重:??$f^{[l]}xf^{[l]}xn_c^{[l-1]}xn_c^{[l]}$ bias:$n_c^{[l]}: (1, 1,1,n_c^{[l]})$ |
Input: $n_H^{[l-1]}xn_w^{[l-1]}xn_c^{[l-1]}$ Output: $n_H^{[l]}xn_w^{[l]}xn_c^{[l]}$ $n_H^{[l]}=\left \lfloor \frac{n^{[l-1]}_H+2p^{[l]}-f^{[l]}}{s^{[l]}} \right \rfloor+1$ $A^{[l]}=mxn_H^{[l]}xn_w^{[l]}xn_c^{[l]}$ |
八、pooling池化操作
最大池 对提取的特征值,保留某区域内的最大值
例:用一个2*2的矩阵,每次移动两步,把覆盖区域内的最大值取出放在2*2矩阵的相应位置
把下图4*4看作是特征的集合,也就是某一层反激活值(我觉得是未激活的输入X吧)集合,数字大说明提取了某些特定特征,左上角的结果为9,则可能是垂直边界或者是CAP特征在最大pooling中,只要提取到相应特征,那就会保留它的最大值,如果没有提取到,则对应区域内的最大值也很小(比如右上角)
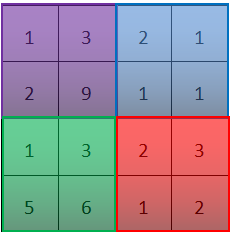 |
运用一个2x2的过滤器 步长为2 |
 |
为什么要用pooling
缩减模型规模,加快计算速度,提高所提取特征的鲁棒性
超参数
pooling中也有一系列超参数,但是并没有必要做梯度下降(这些参数是固定的),一般是手动设置或用正交化方式确定
平均值池:average pooling相较于max pooling,average用的比较少
 |
运用一个2x2的过滤器 步长为2 |
 |
九、卷积神经网络示例(全连接层)
全连接层
在卷积层计算后,将所有卷积结果展开成一维的结果$x$,计算$wx+b$,就是输入的值与输出的结果全连接(就是原来的非卷积层)
一个卷积神经网络的基本层类型:Convolution(CONV卷积层)、Pooling(POOL池化层)、Fully connected(FC全连接层)
例:以识别手写字为例,网络结构为conv1-pool1-conv2-pool2-fc3-fc4-fc5-softmax,(参考了LeNet-5网络)
层的划分:有些会把conv1和pool分成两层,但是因为pool中没有参数,所以分层时以是否有参数来考虑,把conv和pool划分在同一层
fc full connect:全连接层,在第二个pool2后,将所有数据展开(400个值),然后经过fc3会输出120大小的结果(400个值与120个一一对应,全连接),其中有参数w、b
如何选择参数:建议不要自己选,可以多参考文献,别人的选择方式一般卷积神经网络中会包含卷积层、池化层、还有连接层,现在人们还在探索将这三者如何组合会有更好的性能

十、为什么要用卷积神经网络
相对于全连接,卷积的方式使用的参数更少
输入:32x32x3 输出:28x28x6
卷积:32x32x3(=3072输入) * 5x5x3x6 + 6(=456个参数)=28x28x6(=4704输出)
全连接:3072x4704约1400万(个参数)
为什么参数可以比较少?
- 参数共享:一个特征检测器不止在一个位置有用,在其他位置也会有效果。如垂直边界检测,图中可能多个部分都有垂直边界,它们特征相似
- 稀疏连接:一个输出值只依赖于部分输入值,而不是所有。下图为例,结果中左上角的值实际上只需要与输入的左上角的9个值进行连接即可,其它位置的值并不会对这个结果有影响由这两个特性,我们可以用小一些的数据集进行训练,以避免过拟合
translation invariance:卷积神经网络擅于捕捉平移不变,比如把一个猫的图平移两个像素,我们还是可以很清楚地识别出猫。因为把图像平移后,它们还是有相似的特征,所以应该用一样的输出label。用一个filter来生成各层中的像素值,这样可以让学习更健壮,以获得更好的捕捉平移不变特性。


