深度学习——深度学习的实用层面[5]

目录

• 数据集划分
• 偏差和方差
• 判断方差和偏差并调整的基本思想
• 解决高方差问题
• 归一化输入的特征值(X)
• 梯度爆炸/消失
• 用双边导数来进行梯度检验

一、数据集可以划分成三个部分：训练(train)/检验(dev)/测试(test)

在train set上进行训练，在dev上进行验证找出了最好的模型，最后在test进行评估最终模型的性能如何

数据集的划分：一般地，数据量小的时候可以用3:1:1划分，数据量较大时，dev和test的数据占比可以小一些

如果train和dev/test来自不同的源，那么至少要保证dev和test来自相同的分布

二、偏差和方差

training set error	dev set error
1%	11%	high variance 方差较高：过拟合 (在训练集上表现良好， 但是在测试集上表现较差) 出现的原因： 数据有噪声(采集)、训练集不足、 模型训练过度
15%	16%	high bias 偏差过高：欠拟合
15%	30%	high bias & high variance
0.5%	1%	just right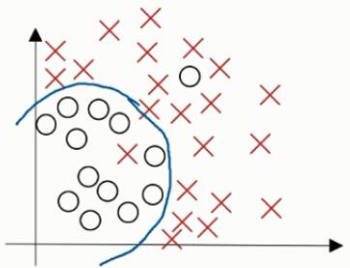

三、判断方差和偏差并调整的基本思想

最优误差：贝叶斯误差  图片分类中，如果train的图像模糊，则可能导致最优误差值较大

偏差和方差的tradeoff

if high bias(training data problem):

　　use bigger network

　　train longer

　　NN architecture search

else(high variance, dev set problem):

　　more data

　　regulation

　　NN architecture search

四、解决高方差问题

• L1/L2正则化：

正则化方法：通过对loss函数添加一个正则项(loss=经验风险+结构风险，系数用来平衡两者)，来对模型复杂度进行约束

给loss函数增加一项L2范数(每一层的$w$范数求和)：$J(w, b)=\frac{1}{m}\sum_i^m{L(\widehat{y}^{(i)},y^{(i)})}+\frac{\lambda}{2m}\sum_{l=1}^L||w^{[l]}||^2_F$

L2范数：向量中各个元素的平方和然后再求平方根$||w||^2_2=\sum_{j=1}^{n_x}w_j^2=w^Tw$

　　　　L2正则化也称为权重衰减，因为w值一直乘以一个小于1的数

$||w^{[l]}||_F^2=\sum_{i=1}^{n^{[l-1]}}\sum_{j=1}^{n^{[l]}}(w_{ij}^{[l]})^2$

$dw^{[l]}=(from backprop) + \frac{\lambda}{m}w^{[l]}$

$w^{[l]}:=w^{[l]}-\alpha dw^{[l]}=(1-\frac{\alpha \lambda}{m})w^{[l]}-\alpha (from backprop)$

L0范数：非0的个数。为了让loss小一些，则参数中非0个数也要少一些，也就是0多一些，即让向量w稀疏

L1范数：向量w中各个元素的绝对值之和$||w||_1=\sum_{j=1}^{n_x}|w_j|$。L0范数不易优化

$\lambda$正则化参数

为什么L2正则化可以消除高方差的问题

直观上如果入值很大，为了最小化$J$，那么$W$的值就会趋近于0，则很多隐藏单元的效果就会被消除，网络会变得很简单

$\lambda$变大，$W$变小，z的取值在如下红色区域内，则g(z)就会变成线性（每一层变成线性），也就不可能作出复杂的决策

常见正则化方法：

L0范数：约束参数中非0的个数，非凸

L1范数(Lasso)：约束绝对值求和，不能直接求导

L2正则(ridge regresson)：参数值2次方求和，凸函数

P范数：P次方

 

• dropout正则化（随机失活）

工作方式：遍历每一层并设置消除节点的概率，从而把网络精简，再进行训练

为什么：开始是希望不要过分依赖于某个参数，dropout作用与L2正则化类似，一般可以用于输入范围比较不同的情况

keep-prob的设置：每一层的keep-prob可以设置不同。如果节点数比较少（过拟合的可能性比较小），则该值可以大一点

缺点：代价函数不能被明确定义，因为每次会随机丢弃一些节点，不便于调试（可以先把dropout关闭，保证J是下降的）

dropout方法在CV中的应用比较多，一般在test阶段不会使用

常用的实施方法：反向随机失活(invented dropout)

第$l$层：$l=3$, keep-prob=0.8

//随机生成一个true/false矩阵，其中每个值为true的概率为0.8（keep-prob保留节点的概率）

d3=np.random.rand(a3.shape[0], a3.shape[1])

a3=np.multiply(a3,d3)

//这一步是inverted dropout：通过除来保持a3的期望值不变

//因为上一步中a3的结果可能会消除一些节点

// 原来a3中所有值的平均为sum/n;随机dropout后sum'=0.8sum，相应的n'=0.8n，才能保证期望不变 

a3/=keep-prob

• 增大数据集

由于直接收集数据的代价会大一点，那么可以通过对原有数据进行变形来增加数据量

• early stopping

随着迭代次数增加，train上的错误率会下降，而dev的错误会可能会先降后升，可以在dev的最低点停止

五、归一化输入的特征值(X)

train和test都应该用同样的$u$和$\sigma$作同样操作

零均值化：$u=\frac{1}{m}\sum_{i=1}^{m}x^{(i)}$，$x:=x-u$

归一化方差：$\sigma^2=\frac{1}{m}\sum^m_{i=1}x^2_{(i)}$，$x:=x/\sigma$

为什么归一化

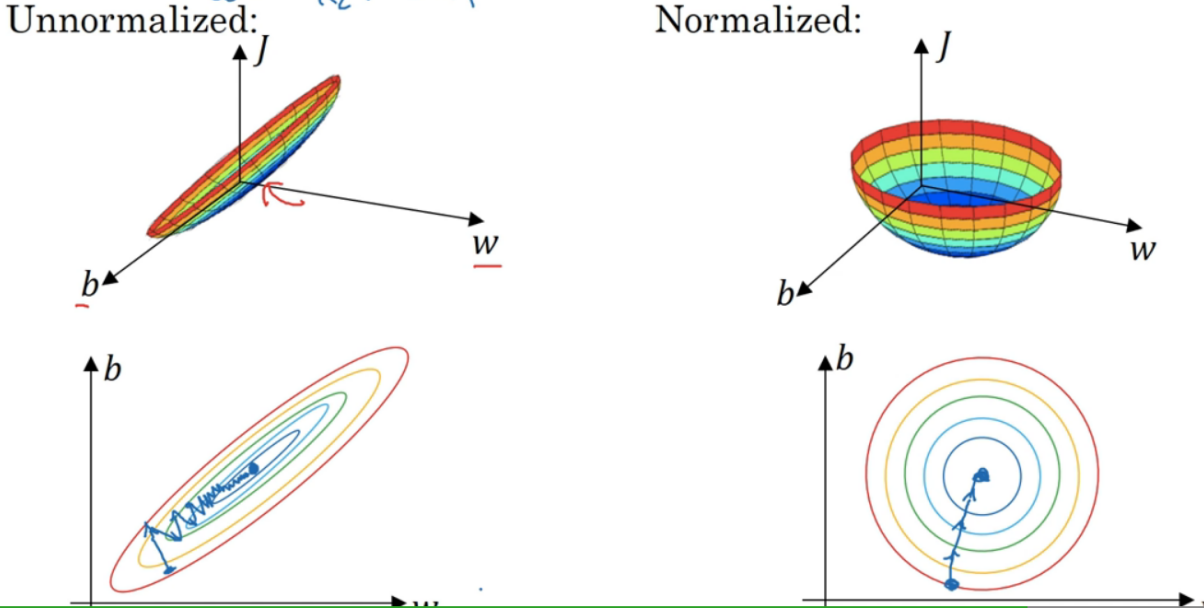
通过归一化处理，使得X的各个特征值取值在相似的范围内，有利于梯度下降的执行加快速度，每次梯度下降时可以用大一点的步长，不像未归一化时，后期的步长就要很小了

为什么未归一化时，$J$的图会是这种狭长的？因为如果一个$x$大，一个$x$小。对于当$J$取到同一个值（等势面），则大$x$对应的$w$就要小一点，而小$x$对应的$w$就要大一点

当特征值的取值范围差很多时，归一化是有必要的

六、梯度爆炸/消失

• 导数指数增加/减小
• 当w大于单位矩阵或小于单位矩阵  vanish/explode

令$g(z)=z$且$b=0$，则$\widehat{y}=w^{[l]}a^{[l-1]}+b^{[l]}=w^{[l]}w^{[l-1]}...w^{[1]}x$

若$w^{[l]}$是1.5倍的单位矩阵，则$\widehat{y}=w^{[1]}\begin{bmatrix}1.5 & 0\\ 0 & 1.5\end{bmatrix}^{[l-1]}x$

会成梯度增长。反之，$\frac{d\widehat{y}}{dw^{[1]}}$梯度下降

• 避免爆炸/消失的方法：初始化w时，让它是与n层数有关，让w随n增加而变小

如$w^{[l]}=random*\sqrt{\frac{2}{n^{[l-1]}}}$

七、用双边导数来进行梯度检验grad check

在反向求导中可以进行梯度检验的测试来保证求导是正确的

• 双边求导

$g(\theta)=\frac{f(\theta + \epsilon)-f(\theta - \epsilon)}{2\epsilon}$

• 梯度检验

对每个参数$\theta_i$，$d\theta_{approx}^{[i]}=\frac{J(\theta_1,\theta_2...,\theta_i+\epsilon,...)-J(\theta_1,\theta_2...,\theta_i-\epsilon,...)}{2\epsilon}\\ \approx d\theta[i]=\frac{dJ}{d\theta_i}$

检查$||d\theta_{approx}-d\theta||_2$和$||d\theta_{approx}+d\theta||_2$的差值($\epsilon=10^{-7}$)

• 梯度检验实现的注意点
  • 不要在训练时使用，只应该用于debug
  • 如果发现算法grad check失败，考虑在算法模块中识别bug
  • 记住正则化
  • 不要和dropout一起使用，因为可能有些节点会被消除
  • 在随机初始化参数并训练一段时间后进行梯度检验。因为有可能在$w$和$b$接近0时，梯度结果正确，而当和0差较大时，梯度结果不正确(这种情况不太多)