【hihoCoder】1033: 交错和
初探数位dp 介绍了数位类统计的基础知识。以下列出其中的基础点:
基本问题
统计在区间[l, r]中满足条件的数的个数
思路
1. [l, r] 将问题转换为 在[0, r]中满足条件的个数 - 在[0, l)满足条件的个数
2. 求解 区间[0, n]满足条件的个数
- 性质:一个小于n的数m,一定是从高位到低位在某一位小于n的对应位的一个数
|
- 遍历所有小于n的数:从高位到低位枚举第一次小于n的数位,之后数位的值就不受限制了
|
- 遍历可以构成一棵树,类似深度优先遍历。第一个图是小于35的数,第二个图是一般情况,i+1的数位比i的大
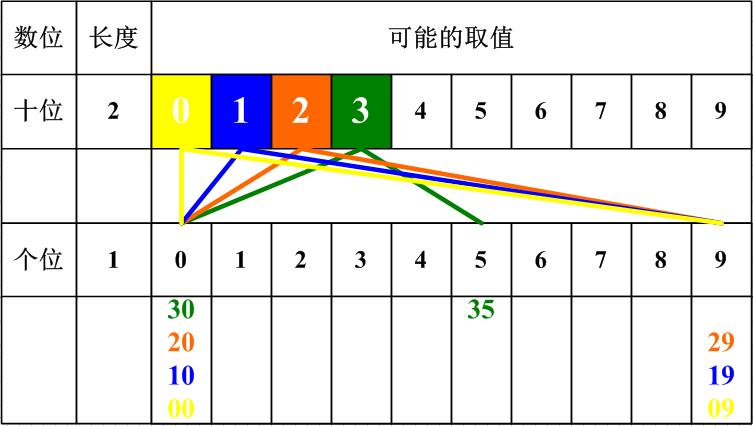
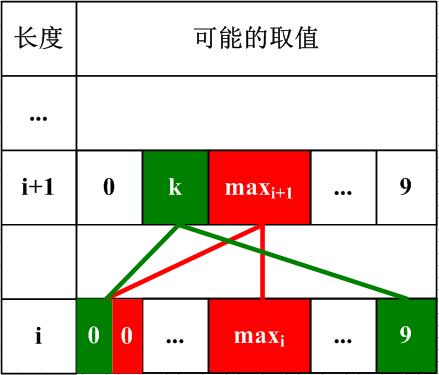
- 递归计算区间[0,n]中满足条件的数
|
F[i, digit, st]表示长度为i,第i位的位为digit,且满足条件st的数的个数。F[i, digit, st] = F[i, digit, st] + F[i-1, digit', st']
- 动态规划:函数的参数表明了一个状态
1 void dp(int 当前数的长度len, int 当前数位的值 digit, bool 当前数前面数位都是0 begin_zero, bool 下一个数位的值有限制 islimit) 2 { 3 if(len == 1)//当前数的长度为1 4 { ...//直接讨论返回 5 return; 6 } 7 //遍历下一位的所有取值情况 8 int maxValue = (islimit?n[len]:9);//下一位的最大取值 9 for(int i = 0; i <= maxValue; i++) 10 { 11 bool _begin_zero = (i == 0 && begin_zero); 12 bool _islimit = (i == maxValue); 13 dp(len - 1, i, _begin_zero, _islimit); 14 } 15 }
Tips:
- 假设区间[0, n]中n的位数为 len(n),初始要从len(n)+1开始。这样对第len(n)位讨论的时候就可以和其它位一样。
- 计算过程中,只有当数位的值没有限制时才把结果存入F[i, digit, st]中,否则会缺失一些结果
- 前面的数位都为0和不全为0需要作为两种状态存储
源码 http://hihocoder.com/problemset/problem/1033

1 #include<iostream> 2 using namespace std; 3 4 #define ll long long int //需要用long long 来进行存放 5 const int mod = 1000000007;//结果的最大值,用于取模 6 struct node{ 7 ll s, n;//s: 各数位交错和 n:满足条件的个数 8 }; 9 node dp[21][20][400];//[长度][以哪个数作为开头][该数的数位交错和] 10 int bits[21];//存放一个数的各位,低到高存放在0到20 11 ll base[21];//每一数位的基准 比如十位数=base[2]=10 12 13 //len数位长度, dig是首个数字, begin_zero表示从最高位到当前位是否全部为0, limit表示下一位枚举是否有限制(bit[len-2]或9), sum是要求的数字和 14 node dfs(int len, int dig, bool begin_zero, bool limit, int sum){ 15 node t;//存放长度为 len的结果 16 t.s = 0, t.n = 0; 17 //超过边界值 18 if (len <= 0 || len >= 20 || dig < 0 || dig > 9 || sum < -200 || sum >= 200) 19 return t; 20 //返回已有的DP结果,即记忆化搜索 21 if (!limit && dp[len][dig + (begin_zero ? 0 : 10)][sum + 200].n != -1) 22 return dp[len][dig + (begin_zero ? 0 : 10)][sum + 200]; 23 //长度只有一位,就不需要枚举下一位了,直接讨论返回即可 24 if (len == 1){ 25 if (dig != sum) 26 return t; 27 t.n = 1, t.s = sum; 28 return t; 29 } 30 //开始枚举下一位的数字 31 int end = limit ? bits[len - 2] : 9;//下一位数字的最大值 32 int newsum = dig - sum; 33 node tmp; 34 for (int j = 0; j < end + 1; j++) 35 { 36 if (begin_zero){//前面都是0,接下来的就由当前位决定 j是否为0 37 tmp = dfs(len - 1, j, j == 0, limit && (j == end), sum); 38 } 39 else{//前面不是全为0 40 tmp = dfs(len - 1, j, false, limit && (j == end), newsum); 41 } 42 //将tmp的值累加到t上 43 t.n += tmp.n;//满足条件的个数 44 //计算满足条件的长度为 len 的data[len]所有数的和, tmp 是长度为 i-1的data[len-1]所有数的和 45 //每一个: data[len] = dig * base[len] + data[len-1] 且共有n个 46 //t.s = t.s + tmp.n * (dig * base[len]) + tmp.s 增加 %mod 就得到下面的结果 47 t.s = ((t.s + tmp.s) % mod + ((tmp.n * dig) % mod * base[len]) % mod) % mod; 48 } 49 //当长度为len,且以dig开头的,数位和为sum 的所有结果都计算完成,才将其进行存储 50 if (!limit) 51 dp[len][dig + (begin_zero ? 0 : 10)][sum + 200] = t; 52 //dig + (begin_zero ? 0 : 10) 用来区分两种状态,(1. 前导都为0;2. 前导包含其它数) 53 return t; 54 } 55 56 int solve(ll n, int s){ 57 if (n <= 0) 58 return 0; 59 int l = 0; 60 for (int i = 0; i < 21; i++) 61 bits[i] = 0; 62 //将n的每一位从低到高放到 bits[0]到bits[l] 中 63 while (n){ 64 bits[l++] = n % 10; 65 n /= 10; 66 } 67 //从l+1开始,比n的长度大1,并且第l+1位数置为0 68 return dfs(l + 1, 0, true, true, s).s; 69 } 70 71 int main(){ 72 ll l, r, s; 73 node t; 74 t.n = -1; 75 t.s = 0; 76 for (int i = 0; i < 21; i++)//长度 77 for (int j = 0; j < 20; j++)//第i位的取值 78 for (int k = 0; k < 400; k++)// i到0 所有位上的交错和 + 200 79 dp[i][j][k] = t; 80 base[1] = 1; 81 for (int i = 2; i < 21; i++)//base 是作为基准数 比如两位数需要 *10, 三位数需要*100 82 base[i] = base[i - 1] * 10 % mod; 83 cin >> l >> r >> s; 84 cout << (solve(r, s) - solve(l - 1, s) + mod) % mod << endl; 85 return 0; 86 }


