进一步解析二分搜索树的实现

二分搜索树的实现核心

• 定义一个类，泛型继承可比较性

public class Tree<E extends Comparable<E>> 

• 私有类作为节点，包括两个子节点

private class Node{
          public E e;
          public Node left,right;
          public Node(E e){
              this.e=e;
              right=null;
              left=null;
          }
    //每个节点
    private Node root;
    //存储数的个数
    private int size; 

• 二分搜索树递归实现（此部分理解较难，下面会具体分析）：

    //对外公开的插入方法，对元素不进行任何处理，直接交给私有的add方法处理
    public void add(E e){
          root=add(root,e);
    }
    //向node为根的二分搜索树插入元素e，递归算法
    private Node add(Node node,E e){
          if (node==null){
              size++;
              return new Node(e);
          }
          if (e.compareTo(node.e)<0)
              add(node.left,e);
          else if (e.compareTo(node.e)>0)
              add(node.right,e);
          return node;
    }

此上为二分搜索树中最核心的代码，以下是我对此代码的理解：

tree类中的泛型有了限制，拿到的数据类型具有可比较性，不继承不能使用compareTo方法，要不会报错。拿到的元素是需要与每个节点进行比较，所以泛型要继承Comparable（对于泛型结尾会简介一下）。

重点来了：私有类node作为节点，e为元素，left，right作为两个子节点，每个私有类先认为他是一个最简单的二叉树，每向下一层就可以把上一层俩子节点当作父节点，那么又可以认为是两个二叉树。这么说可能有点绕，看图就好理解了

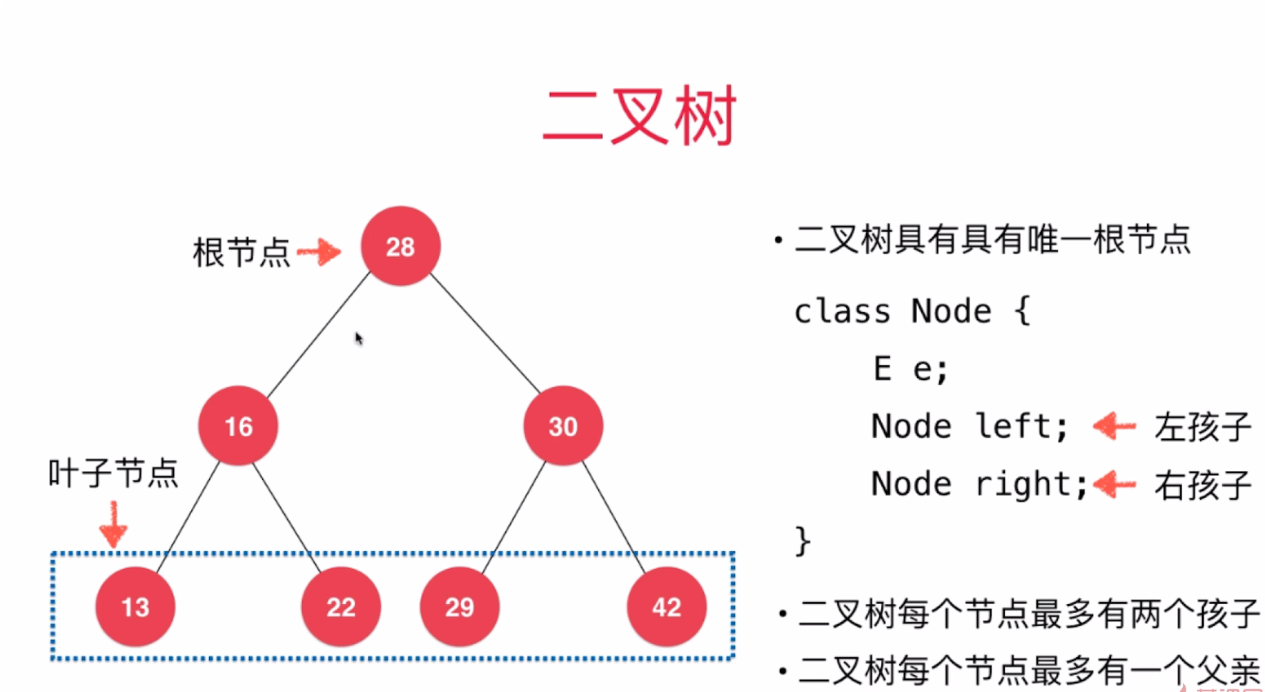
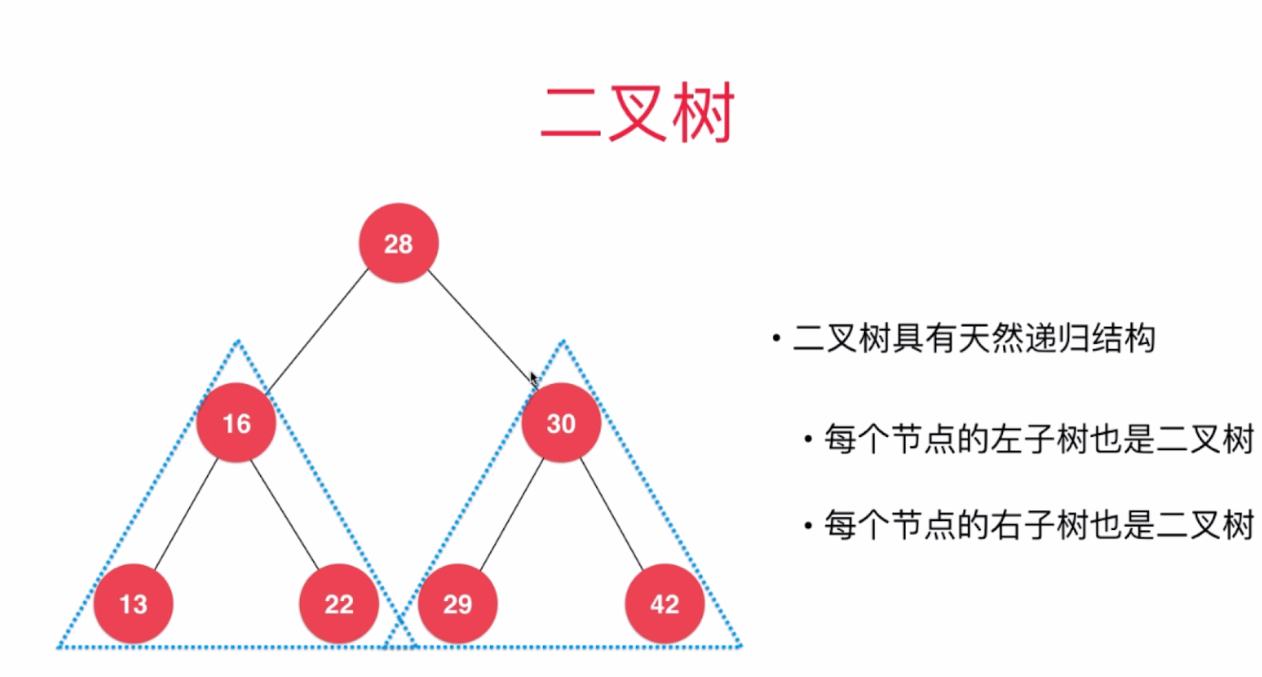
上面的第三段代码看不懂我们先写一个简单的代码理解

 //插入根元素
    public void add(E e){
        if(root==null){
           root=new node(e);
           size++;
        }
          
        else
            add(root,e);
    }
    

此代码看起来就比较简单，如果根节点为空，将元素e插入根节点，长度+1，否为调用子节点

 //向node为根的二分搜索树插入元素e，递归算法
 private void add(Node node,E e){
     if(e.equals(node.e))
         return;
     else if(e.compareTo(node.e)<0&&node.left==null){
         node.left=new node(e);
         size++;
         return;
     }
        
      else if(e.compareTo(node.e)>0&&node.right==null){
          node.right=new node(e);
          size++;
          return;
      }
        
     if(e.compareTo(node.e)<0)
         add(node.left,e);
     else
         add(node.right,e);
 } 

if(e.equals(node.e)) 判断e是否和节点相等，相等不做处理返回。

else if(e.compareTo(node.e)<0&&node.left==null)判断e如果小于节点且左子节点为空，则插入左子节点，长度+1，下句判断则反之。

if(e.compareTo(node.e)<0)判断e小于节点且左子节点不为空，继续向左子树插入元素e，长度+1，下句判断则反之。

上面第三段的代码则是简化后的样子，那么下面我们分析一下它，如果没看懂就用简单的方法，两者原理相同：

root=add(root,e)拿到元素e直接交给私有类add处理。

if (node==null)判断当前节点（包括根节点）是否为空，空的话插入元素，长度+1，返回；

if (e.compareTo(node.e)<0)判断e是否小于当前节点，小于的话继续向左子树插入元素e，直到找到当前节点为空，也就是执行到 if (node==null)中代码（递归）。

if (e.compareTo(node.e)>0)判断e是否大于当前节点，大于的话继续向右子树插入元素e，直到找到当前节点为空，也就是执行到 if (node==null)中代码（递归）。

return node;正常是不会执行此句代码的，一般都会在 if (node==null)中返回，但Node类必须要有返回值，所以加上此句。

二分搜索树的三种遍历

下面再介绍一下前序遍历，中序遍历和后序遍历（用到栈的原理，先入后出）：

前序遍历：根节点先入栈，出栈将右，左子节点分别入栈，左节点出栈，如果左，右子代节点都不为空，继续入栈，左子代节点出栈，直到子代节点都为空，最后入栈的右子代节点出栈，若其有子代节点则继续入栈按以上规律出栈，直到全部出栈。说到这都晕了吧，那么下面看几张图结合理解。

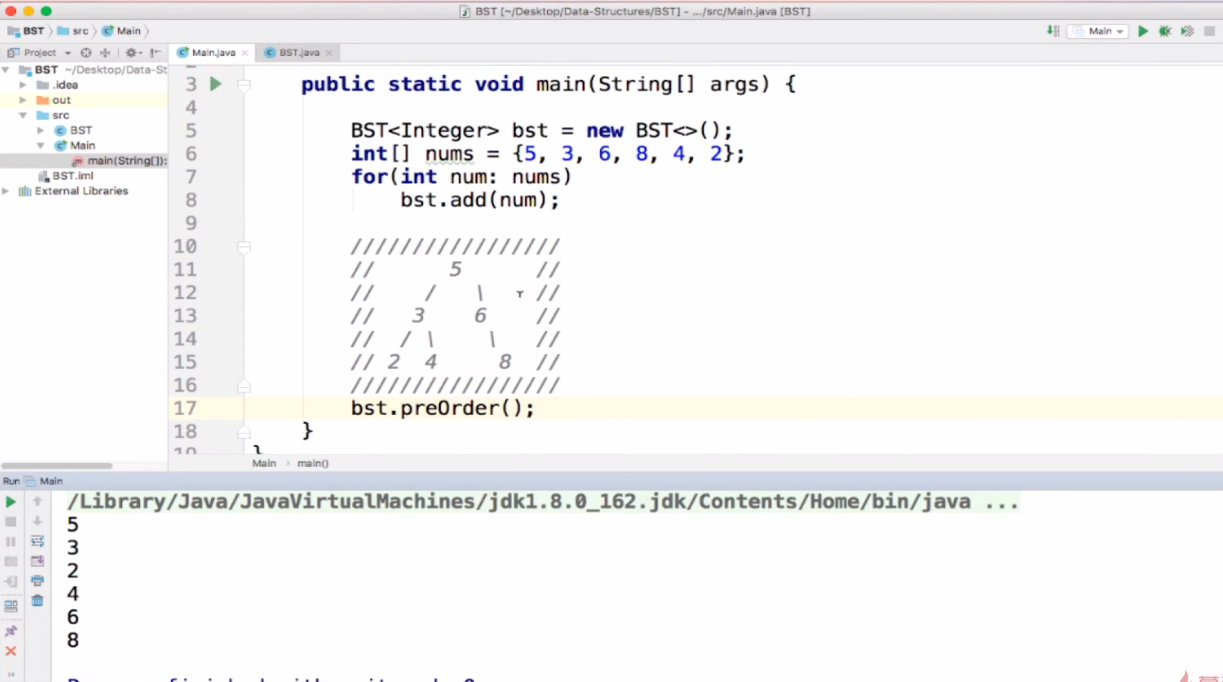
如果栈的说法不明白，那么我们简单来说一下上图的例子：先第一次访问节点（5）打印，再访问该节点左子树，第一次访问节点（3）打印，该节点无子树，第一次访问左子节点（2）打印，无子节点访问结束。然后返回上一层第二次访问节点（3）什么都不做，访问该节点右子节点，第一次访问节点（4）打印，返回上一层第三次访问节点（3）什么都不做，再返回上一层第二次访问节点（5）什么都不做，访问右子树节点（6）将其打印，虽然访问无子树点和左子节点，但是返回后节点（6）依然再被第二次访问，第一次访问节点（8）将其打印，返到到最顶层第三次访问（5）（6）什么都不做。

节点（2）（4）（8）也被访问了三遍，第一遍被打印出来并且没有子节点，所以省略没说。

每个节点都可以认为是一个新的根节点，遍历完自身，才能返回上一层遍历右子树，不知道这样能不能理解（多读几遍理解一下这句话的涵义）。

中序遍历：和上图例子一样，但是第二次访问才将其打印，第一次第三次什么都不做，所以打印出来是234568。

后序遍历：依然同上，是第三次访问才将其打印，第一次第二次什么都不做，所以打印是243865。

总结：可以看出中序遍历可以给序列排序。

先说到这，有不懂的我们可以在评论区交流或私信，如果觉得我说法不对，也欢迎留言相告！

上一篇：走进二分搜索树的第一课