走进二分搜索树的第一课

声明：首先我们要有树的概念，可以查阅资料先做了解。

进去正题：

二分搜索树，是基于二叉树的一种数据结构，与递归有着千丝万缕的联系，为什么这么说呢？

首先我们先了解一下什么是二叉树？

如图一个满的完全二叉树

每个节点的左右子树都是一个二叉树，也就符合递归的特点。更具体一点，接下来深入了解二分搜索树的实现，更能体会递归在其中起到的作用。

了解什么是二分搜索树？

二分搜索树并不是一定是一个满的二叉树，以下二叉树均可作为搜索树的结构

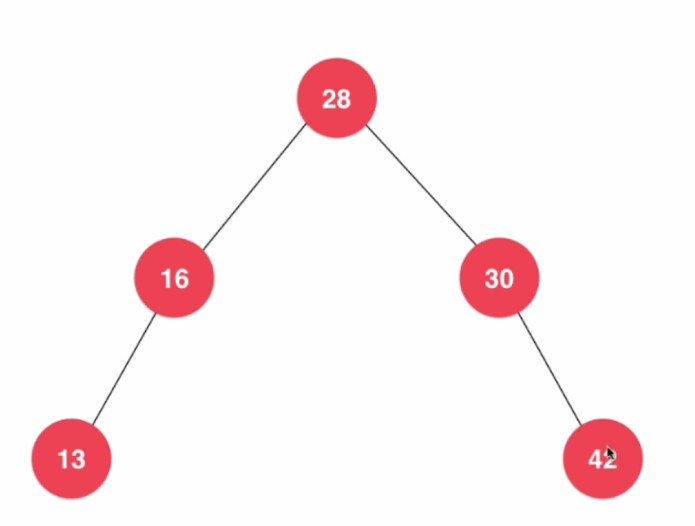
二分搜索树的规律：每个节点值大于左子树所有值，小于右子树所有值，通过图会更清晰的了解

二分搜索树怎么实现存储数据？

假设存入一堆数字

首先如果根节点为空，第一个数就会插入到根节点上，第二数会与第一个数进行对比，小于会放到此二叉树的左子节点，大于则会放在右子节点上，以此类推。

二分搜索数和数组、链表进行比较

二分搜索树和数组（静态数组，动态数组），链表都可作为存储空间，那么它的优势在哪呢？（对于优势当然是指添加，删除，修改，遍历元素的性能）

相对于数组：在数组中往中间添加一个数，它会让使后面的数字分别向后移动一个位置，中间删除一个数，后面的数字分别会前移动一个位置，大大降低性能，而遍历所数涉及数学推理不做过多解释，可以自己试验打印一下遍历所需的时间，建议随机生成上万的数字，更能看到性能的差异。但对于修改或查询一个明确索引的数字，数组会比二分搜索树性能快，毕竟数组的索引起到了重大作用，让时间复杂度仅是O(1)。

声明：不算在数组末尾添加，删除一个数，毕竟在实际应用中不能确定添加，删除操作一定在末尾。

相对于链表：这么说吧，二分搜索树最差的一种情况就是一个线性链表，图上就有一个二分搜索树就是一个线性链表的形状。但这种概率是极低的。

二分搜索数的实现代码

具体实现二分搜索树的代码：

package com.BST;

public class Tree<E extends Comparable<E>> {
      private class Node{
          public E e;
          public Node left,right;
          public Node(E e){
              this.e=e;
              right=null;
              left=null;
          }
      }
      private Node root;
      private int size;
      public Tree(){
          root=null;
          size=0;
      }

    public int getSize() {
        return size;
    }
    public Boolean isEmpty(){
          return size==0;
    }
    //插入根元素
    public void add(E e){
          root=add(root,e);
    }
    //向node为根的二分搜索树插入元素e，递归算法
    private Node add(Node node,E e){

          if (node==null){
              size++;
              return new Node(e);
          }
          if (e.compareTo(node.e)<0)
              add(node.left,e);
          else if (e.compareTo(node.e)>0)
              add(node.right,e);
          return node;
    }

    //看二分搜索树中是否包含元素e
    public boolean contains(E e){
          return  contains(root,e);
    }
    //看以node为底的二分搜索树中是否包含元素e，递归算法
    private boolean contains(Node node,E e){
          if (node==null)
              return false;
           if (e.compareTo(node.e)==0)
               return true;
           else if (e.compareTo(node.e)<0)
              return contains(node.left,e);
           else
              return contains(node.right,e);
      }
    //二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    //前序遍历node为根的二分搜索树，递归算法
    public void  preOrder(Node node){
          if (node==null){
              return;
          }
          System.out.println(node.e);
          preOrder(node.left);
          preOrder(node.right);
    }
    @Override
    public String toString(){
          StringBuilder res=new StringBuilder();
          generateBSTString(root,0,res);
          return  res.toString();
    }

    //生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node,int depth,StringBuilder res){
          if(node==null){
              res.append(generteDepthString(depth)+"null\n");
              return;
          }
          res.append(generteDepthString(depth)+node.e+"\n");
          generateBSTString(node.left,depth+1,res);
    }
    //打印树的深度
    private String generteDepthString(int depth){
          StringBuilder res=new StringBuilder();
          for (int i=0;i<depth;i++){
              res.append("--");
          }
        return res.toString();
    }
    //二分搜索树的中序遍历
    public void inOrder(){
          inOrder(root);
    }
    //中序遍历node为根的二分搜索树，递归算法
    private void inOrder(Node node){
          if (node==null)
              return;
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }
    //二分搜索树的后序遍历
    public void postOrder(){
          postOrder(root);
    }
    private void postOrder(Node node){
          if (node==null)
          return;
          postOrder(node.left);
          postOrder(node.right);
          System.out.println(node.e);
    }
}

下一篇：进一步解析一下代码的实现