二叉树

一.展示

1.1. 代码

#include<stdio.h>
#include<stdlib.h>
#define max 100000

typedef struct binaryTree {
	struct binaryTree* lchild, * rchild;
	char vaule;
}BT;

BT* queen[max];
int front = 0, rear = 0;

//初始化
void init(BT** bt) {
	*bt = (BT*)malloc(sizeof(BT));
	(*bt)->lchild = (*bt)->rchild = NULL;
}

//判断是否为空
int isEmpty(BT* bt) {
	return bt ? 1 : 0;
}
//建立二叉树1
void createBinaryTree(BT** bt) {
	char ch;
	scanf("%c", &ch);
	if (ch == '#') *bt = NULL;
	else {
		*bt = (BT*)malloc(sizeof(BT));
		(*bt)->vaule = ch;
		createBinaryTree(&((*bt)->lchild));
		createBinaryTree(&((*bt)->rchild));
	}
}

//建立二叉树2
BT* createBinaryTree1(BT* bt) {
	char ch;
	scanf("%c", &ch);
	if (ch == '#') bt = NULL;
	else {
		if (!bt) {
			bt = (BT*)malloc(sizeof(BT));
			bt->lchild = bt->rchild = NULL;
		}
		bt->vaule = ch;
		bt->lchild = createBinaryTree1(bt->lchild);
		bt->rchild = createBinaryTree1(bt->rchild);
	}
	return bt;
}

//先序遍历
void preorderTraversal(BT* bt) {
	if (bt) {
		printf("%c", bt->vaule);//改一个地方就成了另外两种遍历方式——中序和后序
		preorderTraversal(bt->lchild);
		preorderTraversal(bt->rchild);
	}
}

//层序遍历
void sequenceTraversal(BT* bt) {
	queen[rear] = bt;
	rear++;
	while (rear - front != 0) {
		printf("%c", queen[front]->vaule);
		if (queen[front]->lchild) queen[rear++] = queen[front]->lchild;
		if (queen[front]->rchild) queen[rear++] = queen[front]->rchild;
		front++;
	}
}

//复制二叉树
BT* copy(BT* copyBt, BT* copiedBt) {
	if (copiedBt) {
		if (!copyBt) {
			copyBt = (BT*)malloc(sizeof(BT));
			copyBt->lchild = copyBt->rchild = NULL;
		}
		copyBt->vaule = copiedBt->vaule;
		copyBt->lchild = copy(copyBt->lchild, copiedBt->lchild);
		copyBt->rchild = copy(copyBt->rchild, copiedBt->rchild);
	}
	return copyBt;
}

//求层数
int depth(BT* bt) {
	int n, m;
	if (!bt) return 0;
	else {
		n = depth(bt->lchild);
		m = depth(bt->rchild);
		if (n > m)
			return n + 1;
		else
			return m + 1;
	}
}

//求节点个数
int nodeCount(BT* bt) {
	if (!bt) return 0;
	return nodeCount(bt->lchild) + nodeCount(bt->rchild) + 1;
}

//求叶子节点
int leavesCount(BT* bt) {
	if (!bt)
		return 0;
	if (!bt->lchild && !bt->rchild)
		return 1;
	else
		return leavesCount(bt->lchild) + leavesCount(bt->rchild);
}

//ABC##DE#G##F###
int main() {
	BT* bt = NULL;
	init(&bt);
	createBinaryTree1(bt);
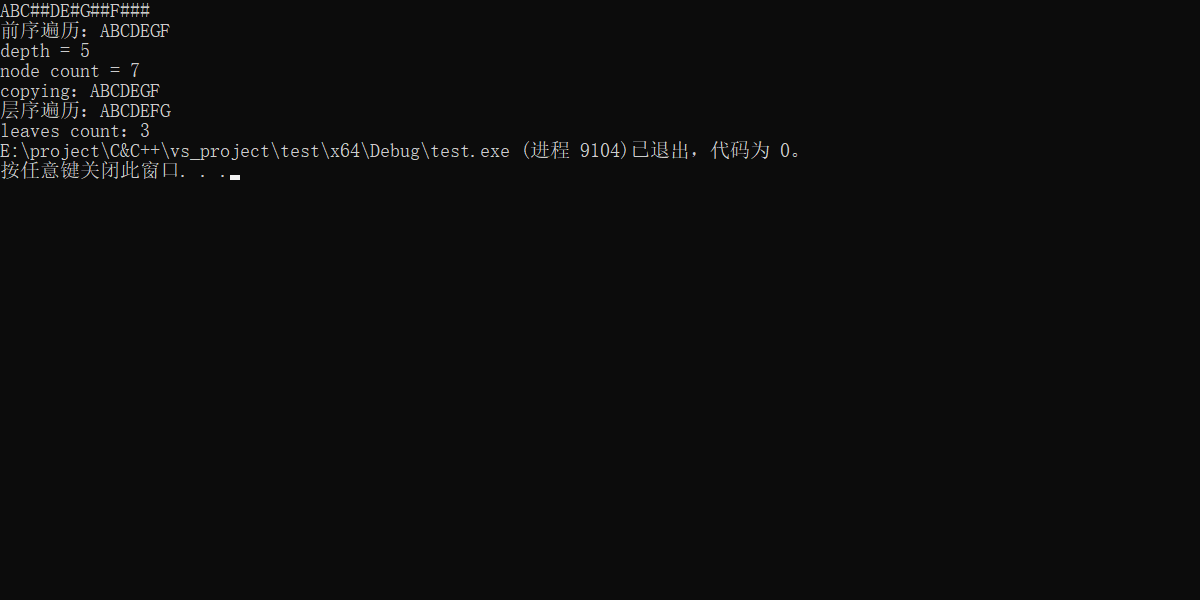
	printf("前序遍历：");
	preorderTraversal(bt);
	printf("\ndepth = %d", depth(bt));
	printf("\nnode count = %d", nodeCount(bt));
	BT* copyBt = NULL;
	init(&copyBt);
	copy(copyBt, bt);
	printf("\ncopying：");
	preorderTraversal(copyBt);
	printf("\n层序遍历：");
	sequenceTraversal(bt);
	printf("\nleaves count：%d", leavesCount(bt));
	return 0;
}

1.2.结果

二.心得

1.建立一个二叉树

因为单独的一个前序或者中序或者后序遍历法不能唯一的确定一个二叉树，但如果能用一种表示方法去将所有节点包括其左右子树的空节点也全部表示出来，那么便能唯一表示一颗二叉树。

例如：测试用例：ABC##DE#G##F###

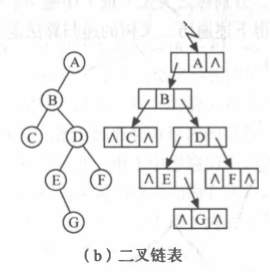
2.遍历二叉树

遍历有四种遍历方式：前序、中序、后序、层序四种遍历法

3.复制二叉树

按前序遍历的方式对应复制

4.求层数

递归找到左右子树的层数，取较大者+1

5.求节点个数

递归找到左右子树的节点个数，左子树个数+右子树+1

6.求叶子节点个数

递归找左右子树的叶子节点，左子树叶子节点个数+右子树叶子节点个数