[hdu-6865]Kidnapper's Matching Problem 线性基+KMP 2020多校8

【题目链接】http://acm.hdu.edu.cn/showproblem.php?pid=6865

【题意】

给出两个数组A B 和集合S，分别有n,m,k个数，n (1≤n≤2⋅10^5), m (1≤m≤min(n,5⋅10^4)) and k (1≤k≤100),

求表达式

 

 

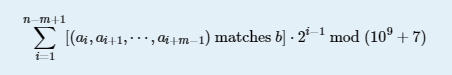
从n中取长度为m的连续一段，每个数字与对应m中的数异或  值如果都在 S集合的异或张成中（张成：一个集合中的数    其异或和的所有可能的结果组成的集合），则matched为1，否则为0.

【题解】

先求出S集合的线性基，然后对A,B集合中的数，消去对应线性基中的位。

则剩下的数如果想满足异或后在S集合中，必须相等。因为余下的位已经无法用线性基表示。

然后就变成了找A串中的B串，用KMP处理

官方证明：

 

 【AC代码】

#include <bits/stdc++.h>
using namespace std;
int const maxn=2e5+7,mod=1e9+7;
const int MAXL = 29,maxn2=5e4+7;
int n,m,k,nex[maxn2];
bool res[maxn];
long long a[maxn],b[maxn2],s[maxn2];
struct LinearBasis{
    long long aa[MAXL+1];
    LinearBasis(){
        std::fill(aa, aa + MAXL + 1, 0);
    }

    void insert(long long t){
        for (int j = MAXL; j >= 0; j--){
            if (!(t & (1ll << j))) continue;
            if (aa[j]) t ^= aa[j];
            else
            {
                for (int k = 0; k < j; k++) if (t & (1ll << k)) t ^= aa[k];
                for (int k = j + 1; k <= MAXL; k++) if (aa[k] & (1ll << j)) aa[k] ^= t;
                aa[j] = t;
                return;
            }
        }
    }

    void build(long long *x, int len){
        std::fill(aa, aa + MAXL + 1, 0);
        for (int i = 1; i <= len; i++){
            insert(x[i]);
        }
    }
}ji;//线性基模板
int main(){
    int t;
    scanf("%d",&t);

    for(int q=1;q<=t;q++){
        scanf("%d%d%d",&n,&m,&k);
        for(int i=1;i<=n;i++){
            scanf("%lld",&a[i]);
        }
        for(int i=1;i<=m;i++){
            scanf("%lld",&b[i]);
        }
        for(int i=1;i<=k;i++){
            scanf("%lld",&s[i]);
        }
        ji.build(s,k);
        //对每一位消去线性基中的位
        for(int i=1;i<=n;i++){
            for(int j=MAXL;j>=0;j--)if(a[i]>>j&1)a[i]^=ji.aa[j];
        }
        for(int i=1;i<=m;i++){
            for(int j=MAXL;j>=0;j--)if(b[i]>>j&1)b[i]^=ji.aa[j];
        }
        long long ans=0;
        //KMP模板
        nex[1]=0;
        for(int i=2,j=0;i<=m;i++){
            while(j&&b[j+1]!=b[i])j=nex[j];//如果前缀匹配不上就一直往前跳到能匹配的前缀，要比只条一次快
            if(b[j+1]==b[i])j++;
            nex[i]=j;
        }
        memset(res,0,n);
        for(int i=1,j=0;i<=n;i++){
            while(j&&b[j+1]!=a[i])j=nex[j];
            if(b[j+1]==a[i])j++;
            if(j==m){
                res[i-m]=1;
                j=nex[j];
            }
        }
        for(int i=n-m;i>=0;i--)ans=(ans*2+res[i])%mod;
        printf("%lld\n",ans);
    }
}