[hdu-6814]Tetrahedron 数学 2020多校5

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6814

题目描述：给定直角四面体的三个直角边长，求高线平方的倒数 1/h^2  

 

 

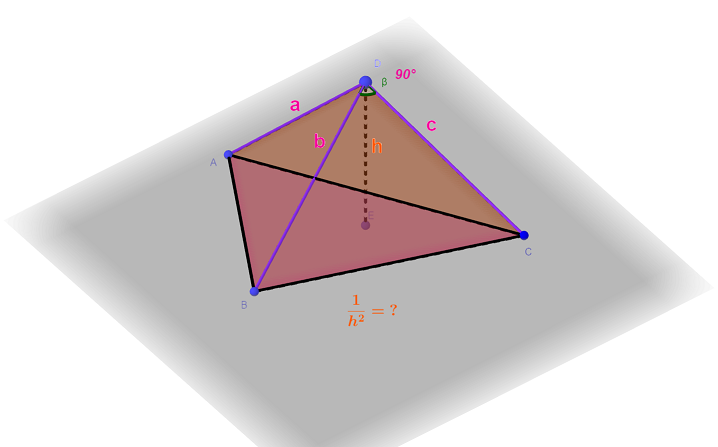
题解：

首先要用到直角四面体

体积 V=abc/6 = Sh/3

 

 

 

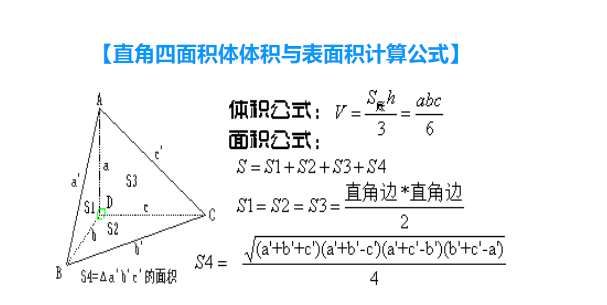
底面积公式

 

 

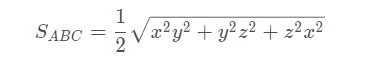
 两公式联立得

 

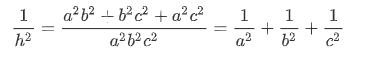
 然后维护下平方逆元的前缀和就行了

期望 E( 1 / h^2 ) = 3 E (1 / a^2 )

 

 PS : 1. 推导底面面积用到了海伦公式 ，具体证明见

https://blog.csdn.net/weixin_43530041/article/details/103147742

2.比赛时候非常智障，我最后一个公式居然没有化到最后一步。。。

AC代码：

#include <bits/stdc++.h>
using namespace std;
int n;
int const maxn=6e6+5,mod=998244353;
long long dan[maxn],ping[maxn];
long long pow_mod(long long a,long long b){
    long long ans = 1ll;
    long long base = a%mod;
    while(b){
        if(b & 1ll) ans = (ans*base)%mod;
        base = (base*base)%mod;
        b >>= 1ll;
    }
    return ans;
}
void init(){
    dan[1]=1;
    ping[1]=1;
    long long u;
    for(int i=2;i<maxn;i++){
        u=pow_mod(i,mod-2);
        dan[i]=u;
        ping[i]=(ping[i-1]+u*u%mod)%mod;
    }
}
int main(){
    int t;
    cin>>t;
    init();
    while(t--){
        int a;
        scanf("%d",&a);
        printf("%lld\n",(3*ping[a]*dan[a])%mod);
    }
    return 0;
}