莫队学习笔记
转载请带上本博客地址:https://www.cnblogs.com/continue126/p/14450059.html
并注明原作者:@博客园:continue_1025,创作不易,请理解。
普通莫队
引入小例
\(zl\) 姐姐有一串数,由于学生化太头秃了,所以现在他想问你 \(m(m≤1e5)\) 次,其中 \(L\) 到 \(R\) 区间出现次数在\(3\)次及以上的数有多少个?
解决方案
线段树
效率低下,不好维护。
(\(p.s.\) : \(lmpp\) 巨佬说如果 \(3\) 次可以取等的话,线段树反而效率更高,巨佬们可以自己尝试,菜比这里就不演示了)
故引入莫队——一种处理区间问题的离线算法。
0.算法名字的由来
莫队算法,其中的“莫”指国家队莫涛巨佬,CCCCOrz。
1.基本原理
莫队是优美的暴力。
先让我们回到开头来帮帮 \(zl\) 姐姐。
\(Continue\) 是个傻子,所以他打了个暴力;
for(int i=l;i<=r;i++)
{
cnt[a[i]]++;
if(cnt[a[i]]>=3)
ans++;
}
如果每次询问都这么打的话,很明显, \(O(nm)\) 的算法是会让 \(zl\) 姐姐难堪的。(\(zl\) 姐姐:你来真的?)
聪明的你捡起了傻子 \(Continue\) 打的暴力,觉得好不容易打的,扔了多可惜啊。
于是你开始对刚刚的暴力结果进行改造。
你想,既然我们已经知道了 \([L,R]\) 的结果,那么 \([L-1,R]\),\([L+1,R]\),\([L,R-1]\),\([L,R+1]\)的结果不就可以也一起很容易得到了吗?
在 \(O(1)\) 的时间里,现在你的手里现在已经有了 \(5\) 个答案。
这是多好的事,于是你将这个性质推广到了所有的询问。
详细的,为了方便,我们不妨将推广得来的四个答案一类称作推广区间,将推广区间们对应的原区间 \([L,R]\) 称作原区间。只要我们知道了原区间的答案,那么要求的推广区间便也就可求了。
所以现在问题就转化为了:“如何使询问区间成为一个推广区间”。进一步地,由于我们无法改变询问,这个问题变成了“如何使推广区间匹配上询问区间”。
显然,我们可以通过不断修改原区间的方式,来匹配与询问区间一致的推广区间。
很明显,这种不断变化范围的操作,我们可以通过 \(while\) 循环实现。
可是如果每次都 \(while\) ,我们的代码仍然是一份傻子代码——会 \(T\) 得惨不忍睹(\(g2020\) \(lvt\) \(&&\) \(dlz\)大佬语)
所以接下来才是真正应用时的莫队:分块+\(sort\)。
2.基本莫队
有了上面的一些推论,现在你意识到,每次询问时都要根据查询区间的大小调整原区间大小,且由于询问区间并不相同(否则该问题将没有意义),所以这个操作是必然的。
在必然的情况下,我们要尽可能的使该操作尽量的快,由此才能做到优美的暴力。
再次分析上面的过程,我们发现该操作的主要时耗来源于锁定所需区间的过程,所以我们应尽可能的将每次需要的推广区间之间的差减小,以此来减少变化区间范围的次数,提高了效率。
而达到此目的的唯一方式就是对查询区间进行排序。
这便是优美莫队里面的\(sort\)部分。
至于排序的标准,自然要依靠于分块啦~
由于我们要求两个区间尽量的相似,所以应满足单调性,不然会浪费时间。
如图。
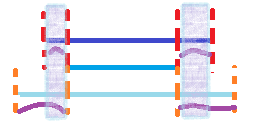
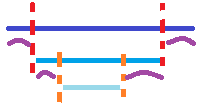
注:紫色曲线代表每次锁定区间时需移动的长度。
图一是未排序的效果,可以看见阴影的部分我们是重复移动了的,这样十分浪费时间。
只要排序成图二这样,要移动的区间就再也不会重叠啦~
确定了排序的任务,那么排序的关键字呢?
答案是分块。
分块合理地将节点划分了不同的区间,这样就可以较快的比较。
我们通过左端点所处的块进行排序,若处于同一个块则比较右端点。这样就可以科学有效的降低时间啦~
3.代码
上面的都懂了,接下来就是一份普通莫队的模板代码,一般的题都可以变着花样套板子。(当然不能算带权莫队树上莫队)
\(Problem\):HH的项链
这道题 \(luogu\) 是卡了莫队的(但还是有神仙巨佬卡过去了),正解是树状数组。故在这里只是作为练手题。A6个点,T4个点就差不多了。主要是思想,思想!
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=2e6+10;
const int inf=1<<30;
inline int Read()
{
int s=0;
int f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
s=(s<<1)+(s<<3)+ch-'0';
ch=getchar();
}
return s*f;
}
int n,m;
struct Num
{
int l,r; //询问的区间
int num; //询问的答案
int id; //询问的次序
}a[maxn];
int temp[maxn];
int bel[maxn]; //belong
bool cmp(Num x,Num y)
{
return ((bel[x.l]==bel[y.l]) && (x.r<y.r)) || (bel[x.l]<bel[y.l]);
}
bool cmp2(Num x,Num y)
{
return x.id<y.id;
}
int cnt[maxn]; //记录次数的数组
int top;
int ans; //答案有几个
inline void Add(int x)
{
cnt[x]++;
if(cnt[x]==1)
ans++;
}
inline void Dele(int x)
{
cnt[x]--;
if(!cnt[x])
ans--;
}
int main()
{
n=Read();
int k=sqrt(n); //分块
for(int i=1;i<=n;i++)
{
temp[i]=Read();
bel[i]=(i-1)/k+1;
}
m=Read();
for(int i=1;i<=m;i++)
{
int x,y;
x=Read();
y=Read();
if(x>y)
swap(x,y);
a[i].l=x;
a[i].r=y;
a[i].id=i;
}
sort(a+1,a+m+1,cmp);
int l=1,r=0;
for(int i=1;i<=m;i++)
{
int x=a[i].l;
int y=a[i].r;
//锁定区间的过程
while(l>x)
Add(temp[l-1]),--l;
while(l<x)
Dele(temp[l]),++l;
while(r<y)
Add(temp[r+1]),++r;
while(r>y)
Dele(temp[r]),--r;
a[i].num=ans;
}
sort(a+1,a+m+1,cmp2); //离线算法按原序输出答案
for(int i=1;i<=m;i++)
printf("%d\n",a[i].num);
return 0;
}
在 \(zl\) 姐姐感激的眼神鼓舞下,更进一步吧!
带权莫队
引入小例
\(zl\) 姐姐有一串数,由于他太可爱了,所以现在原基础上增加一个操作:将第 \(k\) 个数变成 \(num\)。
解决方案
由于现在的问题仍然保留询问操作,所以我们仍考虑使用莫队解决。
由于修改数值的操作,我们需要莫队可以储存数据。由此我们引入一个新的结构:带权莫队。
1.基本原理
带权莫队的基本原理和普通莫队是一样的。
只会打暴力的傻子 \(Continue\) 是这么想的:
只要每次一输入和当前区间有关的修改,就马上暴力修改。
很明显,这会 \(TLE\) ,因为区间可能不定。
这很像最开始我们处理基础莫队时遇到的问题。那么这次同样的,我们使用 \(sort\) 来解决。
我们新增一个关键字 \(tim\) \((time)\) ,其中记录了对当前询问有影响的修改操作的序号。\(sort\) 的时候将 \(tim\) 作为第三关键字,这样既能保证基础莫队对询问操作处理的正确性,又能及时处理修改操作。因为修改操作复杂度低,所以这样就不会 \(TLE\) 了。
修改操作单独建一个结构体, \(perfect\)。
3.代码
\(Problem\):数颜色
这道题题解里面有一个巨佬,在修改操作的时候很神仙的运用了转换的思想,我的代码写得差多了,所以传送门就放在这里,大家可以去看。
这题还是卡莫队,所以分块的块数设置为常数就不会卡了。
很多大佬都是将分块的块数 \(k\) 设置为的 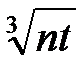 (啊没错这个图是复制的),因为这样最快。其具体证明戳这位大佬的题解,菜比我证不来也看不懂(
(啊没错这个图是复制的),因为这样最快。其具体证明戳这位大佬的题解,菜比我证不来也看不懂(
完。
鸣谢
感谢 \(zl\) 小姐姐不知不觉间提供给我的精神支持。
感谢我自己是个大菜比。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号